Coursera吴恩达机器学习课程笔记——神经网络: 学习（Neural Networks: Learning）

9 神经网络: 学习（Neural Networks: Learning）

9.1 代价函数（Cost Function）

神经网络的分类问题有两种：

• 二元分类问题（0/1分类）

  只有一个输出单元（$K=1$）

• 多元（$K$）分类问题

  输出单元不止一个（$K>1$）

神经网络的代价函数公式：

$h_{\Theta }(x)=a^{(L)}=g({\Theta }^{(L-1)}{a}^{(L-1)})=g(z^{(L)})$

KaTeX parse error: {gather*} can be used only in display mode.

$L$: 神经网络的总层数

$s_l$: 第 $l$ 层激活单元的数量（不包含偏置单元）

$h_{\Theta }(x{)}_k$: 分为第 $k$ 个分类($k^{th}$)的概率 $P(y=k | x ; \Theta) $

$K$: 输出层的输出单元数量，即类数 - 1

$y_k^{(i)}$: 第 $i$ 个训练样本的第 $k$ 个分量值

$y$: $K$ 维向量

注：此处符号表达和第四周的内容有异有同，暂时先按照视频来，有必要的话可以做下统一.

公式可长可长了是吧，但是不是有些熟悉？对照下逻辑回归中的代价函数：

$J(\theta )=-\frac{1}{m}{\sum }_{i=1}^m[y^{(i)}\log (h_{\theta }(x^{(i)}))+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$

在神经网络的代价函数中，

• 左边的变化实际上是为了求解 $K$ 分类问题，即公式会对每个样本特征都运行 $K$ 次，并依次给出分为第 $k$ 类的概率，$h_{\Theta }(x)\in {\mathbb{R}}^K,y\in {\mathbb{R}}^K$。
• 右边的正则化项比较容易理解，每一层有多维矩阵 ${\Theta }^{(l)}\in {\mathbb{R}}^{(s_l+1)\times s_{l+1}}$，从左到右看这个三次求和式 $\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}$ ，就是对每一层间的多维矩权重 ${\Theta }^{(l)}$ ，依次平方后求取其除了偏置权重部分的和值，并循环累加即得结果。

${\mathbb{R}}^m$: 即 $m$ 维向量

${\mathbb{R}}^{m\times n}$: 即 $m\times n$ 维矩阵

再次可见，神经网络背后的思想是和逻辑回归一样的，但由于计算复杂，实际上神经网络的代价函数 $J(\Theta )$ 是一个非凸（non-convex）函数。

9.2 反向传播算法（Backpropagation Algorithm）

类似于回归模型中的梯度下降算法，为了求解神经网络最优化问题，我们也要计算 $\frac{\partial }{\partial \Theta }J(\Theta )$，以此 $\underset{\Theta }{\mathrm{minimize}}J(\Theta )$ 。

在神经网络中，代价函数看上去虽然不复杂，但要注意到其中 $h_{\Theta }(x)$ 的求取实际上是由前向传播算法求得，即需从输入层开始，根据每层间的权重矩阵 $\Theta$ 依次计算激活单元的值 $a$。 在最优化代价函数时，我们必然也需要最优化每一层的权重矩阵，再次强调一下，算法最优化的是权重，而不是输入。

反向传播算法用于计算每一层权重矩阵的偏导 $\frac{\partial }{\partial \Theta }J(\Theta )$，算法实际上是对代价函数求导的拆解。

1. 对于给定训练集 $\{(x^{(1)},y^{(1)})\cdots (x^{(m)},y^{(m)})\}$ ，初始化每层间的误差和矩阵 $\Delta$，即令所有的 ${\Delta }_{i,j}^{(l)}=0$，使得每个 ${\Delta }^{(l)}$ 为一个全零矩阵。

2. 接下来遍历所有样本实例，对于每一个样本实例，有下列步骤：

   1. 运行前向传播算法，得到初始预测 $a^{(L)}=h_{\Theta }(x)$ 。

   2. 运行反向传播算法，从输出层开始计算每一层预测的误差（error），以此来求取偏导。

  输出层的误差即为预测与训练集结果的之间的差值：$\delta^{(L)} = a^{(L)} - y$，

  对于隐藏层中每一层的误差，都通过上一层的误差来计算：

  $\delta^{(l)} = (\Theta^{(l)})^T\delta^{(l+1)} .*\ \frac{\partial a^{(l)}}{\partial z^{(l)}}\; \; \; \; \;  \text{for }l := L-1, L-2,\dots,2.$

  隐藏层中，$a^{(l)}$ 即为增加偏置单元后的 $g(z^{(l)})$，$a^{(l)}$ 与 $\Theta^{(l)}$ 维度匹配，得以完成矩阵运算。

  即对于隐藏层，有 $a^{(l)} = (g(z^{(l)})$ 添加偏置单元 $a^{(l)}_0 = 1)$

  解得 $\frac{\partial}{\partial z^{(l)}}g(z^{(l)})=g'(z^{(l)})=g(z^{(l)}) .* \ (1-g(z^{(l)}))$，

  则有 $\delta^{(l)} = (\Theta^{(l)})^T\delta^{(l+1)} .*\ a^{(l)} .*\ (1-a^{(l)}), \ \ a^{(l)}_0 = 1$。

  > $\delta^{(l)}$ 求导前的公式不同于视频内容，经核实为视频内容错误。推导请阅下节。

  根据以上公式计算依次每一层的误差 $\delta^{(L)}, \delta^{(L-1)},\dots,\delta^{(2)}$。

3. 依次求解并累加误差 ${\Delta }_{i,j}^{(l)}:={\Delta }_{i,j}^{(l)}+a_j^{(l)}{\delta }_i^{(l+1)}$，向量化实现即 ${\Delta }^{(l)}:={\Delta }^{(l)}+{\delta }^{(l+1)}(a^{(l)}{)}^T$

4. 遍历全部样本实例，求解完 $\Delta$ 后，最后则求得偏导 $\frac{\partial }{\partial {\Theta }_{i,j}^{(l)}}J(\Theta )=D_{i,j}^{(l)}$

   • $D_{i,j}^{(l)}:=\frac{1}{m}\left({\Delta }_{i,j}^{(l)}+\lambda {\Theta }_{i,j}^{(l)}\right)$, if $j\ne 0$,
   • $D_{i,j}^{(l)}:=\frac{1}{m}{\Delta }_{i,j}^{(l)}$, if $j=0$.（对应于偏置单元）

${\delta }^{(l)}$: 第 $l$ 层的误差向量

${\delta }_i^{(l)}$: 第 $l$ 层的第 $i$ 个激活单元的误差

${\Delta }_{i,j}^{(l)}$: 从第 $l$ 层的第 $j$ 个单元映射到第 $l+1$ 层的第 $i$ 个单元的权重代价的偏导（所有样本实例之和）

$D_{i,j}^{(l)}$: ${\Delta }_{i,j}^{(l)}$ 的样本均值与正则化项之和

注：无需计算 ${\delta }^{(1)}$，因为输入没有误差。

这就是反向传播算法，即从输出层开始不断向前迭代，根据上一层的误差依次计算当前层的误差，以求得代价函数的偏导。

应用反向传播（BP）算法的神经网络被称为 BP 网络，也称前馈网络（向前反馈）。

《机器学习》一书中提到的 BP 网络强大之处：

任何布尔函数都可由两层神经网络准确表达，但所需的中间单元的数量随输入呈指数级增长;

任何连续函数都可由两层神经网络以任意精度逼近;

任何函数都可由三层神经网络以任意程度逼近。

9.3 直观理解反向传播（Backpropagation Intuition）

这节给出了反向传播算法中误差的数学意义：

$cost(t)=y^{(t)}\log (h_{\Theta }(x^{(t)}))+(1-y^{(t)})\log (1-h_{\Theta }(x^{(t)}))$

${\delta }_j^{(l)}=\frac{\partial }{\partial z_j^{(l)}}cost(t)$

视频内容实际在上文都涉及到了，上节也做了解释：

反向传播算法，即从输出层开始不断向前迭代，根据上一层的误差依次计算当前层的误差，以求得代价函数的偏导。

不过，这块还是有些不好理解，可回顾视频。

前文提到输入层没有偏差，所以没有 ${\delta }^{(1)}$，同样的，偏置单元的值始终为 1，也没有误差，故一般会选择忽略偏置单元项的误差。

神经网络中代价函数求导的推导过程：

代价函数无正则化项时：

KaTeX parse error: {gather*} can be used only in display mode.

再次的，为了方便起见，这里假设样本只有一个，则有：

KaTeX parse error: {gather*} can be used only in display mode.

忆及 $h_{\Theta }(x)=a^{(L)}=g(z^{(L)})$，$g(z)=\frac{1}{1+e^{(-z)}}$，代入后整理后可得：

$J(\Theta )=y\log \left(1+e^{-z^{(L)}}\right)+\left(1-y\right)\log \left(1+e^{z^{(L)}}\right)$

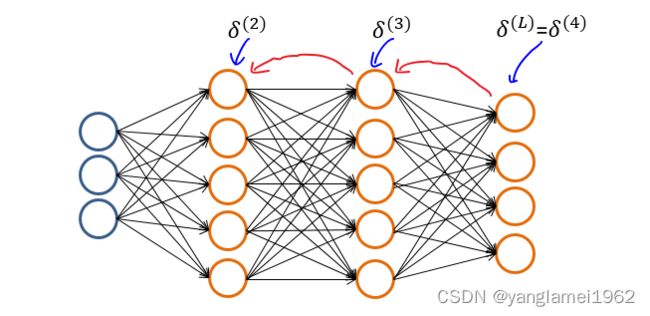
再次为了便于计算，我们用到如上图这个三层（输入层一般不计数）神经网络。

忆及 $z^{(l)}={\Theta }^{(l-1)}{a}^{(l-1)}$，我们有 $h_{\Theta }(x)=a^{(4)}=g(z^{(4)})=g({\Theta }^{(3)}{a}^{(3)})$

观察考虑各变量与 ${\Theta }^{(3)}$ 之间的关系，有 $J(\Theta )\to a^{(4)}\to z^{(4)}\to {\Theta }^{(3)}$

要计算 $J(\Theta )$ 的偏导，就要按照关系不断往前看，每一次回头看，就称为一次反向传播。

把回头看的关系说的“微积分一点”，那就是 ${\Theta }^{(3)}$ 的微小改变会引起 $z^{(4)}$ 的改变， $z^{(4)}$ 的微小改变会引起 $a^{(4)}$ 的改变，$a^{(4)}$ 的微小改变又会引起 $ J(\Theta)$ 的改变，关系方向也可以反过来写：$\Theta^{(3)} \rightarrow z^{(4)} \rightarrow a^{(4)} \rightarrow J(\Theta) $。

如果你还记得微积分（不然你应该也不会看到这里(*^_*)~），听起来像不像在暗示链式求导？

令 ${\delta }^{(l)}=\frac{\partial }{\partial z^{(l)}}J(\Theta )$，则有 $J(\Theta )$ 关于 ${\Theta }^{(3)}$ 的偏导：

$\frac{\partial }{\partial {\Theta }^{(3)}}J(\Theta )=\frac{\partial J(\Theta )}{\partial z^{(4)}}\frac{\partial z^{(4)}}{\partial {\Theta }^{(3)}}={\delta }^{(4)}\frac{\partial z^{(4)}}{\partial {\Theta }^{(3)}}$

再次忆及 $z^{(l)}={\Theta }^{(l-1)}{a}^{(l-1)}$，则 $\frac{\partial z^{(4)}}{\partial {\Theta }^{(3)}}=a^{(3)}$

则对于输出层，我们证得 $\frac{\partial }{\partial {\Theta }^{(3)}}J(\Theta )=a^{(3)}{\delta }^{(4)}$。

再次忆及 $g(z)=\frac{1}{1+e^{-z}}$，$a^{(L)}=g(z^{(L)})$

${\delta }^{(4)}=\frac{\partial }{\partial z^{(4)}}J(\Theta )=y\frac{-e^{-z^{(4)}}}{1+e^{-z^{(4)}}}+\left(1-y\right)\frac{e^{z^{(4)}}}{1+e^{z^{(4)}}}=g(z^{(4)})-y=a^{(4)}-y$

即证得 ${\delta }^{(4)}=a^{(4)}-y$

对于任意的输出层 $L$ 及 ${\Theta }^{(L-1)}$，有 $J(\Theta )\to a^{(L)}\to z^{(L)}\to {\Theta }^{(L-1)}$ 关系不变，故证得：
$$\frac{\partial }{\partial {\Theta }^{(L-1)}}J(\Theta )=a^{(L-1)}{\delta }^{(L)},{\delta }^{(L)}=a^{(L)}-y$$
好了，接下来来看一下 $J(\Theta )$ 关于 ${\Theta }^{(2)}$ 的偏导

仍然观察考虑各变量与 ${\Theta }^{(2)}$ 之间的关系，有 $J(\Theta )\to a^{(4)}\to z^{(4)}\to a^{(3)}\to z^{(3)}\to {\Theta }^{(2)}$

$\frac{\partial }{\partial {\Theta }^{(2)}}J(\Theta )=\frac{\partial J(\Theta )}{\partial z^{(3)}}\frac{\partial z^{(3)}}{\partial {\Theta }^{(2)}}={\delta }^{(3)}\frac{\partial z^{(3)}}{\partial {\Theta }^{(2)}}=a^{(2)}{\delta }^{(3)}$

${\delta }^{(3)}=\frac{\partial }{\partial z^{(3)}}J(\Theta )=\frac{\partial J(\Theta )}{\partial z^{(4)}}\frac{\partial z^{(4)}}{\partial a^{(3)}}\frac{\partial a^{(3)}}{\partial z^{(3)}}={\delta }^{(4)}\frac{\partial z^{(4)}}{\partial a^{(3)}}\frac{\partial a^{(3)}}{\partial z^{(3)}}$

易求得 $\frac{\partial z^{(4)}}{\partial a^{(3)}}={\Theta }^{(3)}$

$g^{\prime }(z)=\frac{e^{-z}}{(1+e^{-z}{)}^2}=\frac{(1+e^{-z})-1}{(1+e^{-z}{)}^2}=\frac{1}{1+e^{-z}}-\frac{1}{(1+e^{-z}{)}^2}=g(z)(1-g(z))$

即 $g^{\prime }(z^{(l)})=g(z^{(l)}).\ast (1-g(z^{(l)}))$

有 $a^{(l)}=(g(z^{(l)})$ 添加偏置单元 $a_0^{(l)}=1)$，则 $\frac{\partial a^{(3)}}{\partial z^{(3)}}=a^{(3)}.\ast (1-a^{(3)})$，

证明时为先求导后添加偏置单元，与前向传播算法顺序一致，实际实现时，求导和添加偏置单元的顺序可作调换，由于一般选择忽略偏置单元的误差，所以并不影响结果。

即证得 ${\delta }^{(3)}=({\Theta }^{(3)}{)}^T{\delta }^{(4)}.\ast (a^{(3)}{)}^{\prime }=({\Theta }^{(3)}{)}^T{\delta }^{(4)}.\ast a^{(3)}.\ast (1-a^{(3)})$

对于任意的隐藏层 $l+1$ 及权重矩阵 ${\Theta }^{(l)}$，有 $J(\Theta )\to a^{(L)}\to z^{(L)}\to \cdots \to a^{(l+1)}\to z^{(l+1)}\to {\Theta }^{(l)}$ 关系不变，故证得：
$$\frac{\partial }{\partial {\Theta }^{(l)}}J(\Theta )=a^{(l)}{\delta }^{(l+1)},{\delta }^{(l)}=({\Theta }^{(l)}{)}^T{\delta }^{(l+1)}.\ast a^{(l)}.\ast (1-a^{(l)})\text{for }l:=L-1,L-2,\dots ,2.$$
再添回为了计算方便去掉的 $\frac{1}{m}$ 和正则化项（时刻记住偏置单元不正则化）等，即可得上节中 $J(\Theta )$ 的偏导。

证明结束，留个课后作业呀，自己来计算一下 $J(\Theta )$ 关于 ${\Theta }^{(1)}$ 的偏导，是不是能得到同样的结果？

9.4 实现注意点: 参数展开（Implementation Note: Unrolling Parameters）

在 Octave/Matlab 中，如果要使用类似于 fminunc 等高级最优化函数，其函数参数、函数返回值等都为且只为向量，而由于神经网络中的权重是多维矩阵，所以需要用到参数展开这个技巧。

说白了，这个技巧就是把多个矩阵转换为一个长长的向量，便于传入函数，之后再根据矩阵维度，转回矩阵即可。

Octave 代码：

% 多个矩阵展开为一个向量
Theta1 = ones(11, 10);    % 创建维度为 11 * 10 的矩阵
Theta2 = ones(2, 4) * 2;  % 创建维度为 2 * 4 的矩阵
ThetaVec = [Theta1(:); Theta2(:)]; % 将上面两个矩阵展开为向量

% 从一个向量重构还原回多个矩阵
Theta1 = reshape(ThetaVec(1:110), 11, 10)
Theta2 = reshape(ThetaVec(111:118), 2, 4)
% Theta2 = reshape(ThetaVec(111:(111 + 2 * 4) - 1), 2, 4)

reshape(A,m,n): 将向量 A 重构为 m * n 维矩阵。

9.5 梯度检验（Gradient Checking）

由于神经网络模型中的反向传播算法较为复杂，在小细节非常容易出错，从而无法得到最优解，故引入梯度检验。

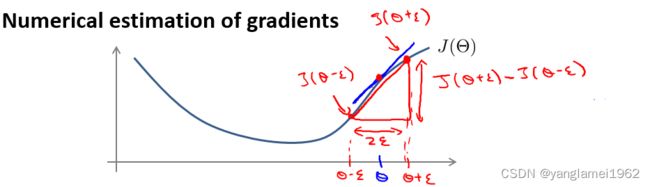
梯度检验采用数值估算（Numerical estimation）梯度的方法，被用于验证反向传播算法的正确性。

把视 $\Theta$ 为一个实数，数值估算梯度的原理如上图所示，即有 $\frac{\partial }{\partial \Theta }J(\Theta )\approx \frac{J(\Theta +ϵ)-J(\Theta -ϵ)}{2ϵ}$

其中，$ϵ$ 为极小值，由于太小时容易出现数值运算问题，一般取 $10^{-4}$。

对于矩阵 $\Theta$，有 $\frac{\partial }{\partial {\Theta }_j}J(\Theta )\approx \frac{J({\Theta }_1,\dots ,{\Theta }_j+ϵ,\dots ,{\Theta }_n)-J({\Theta }_1,\dots ,{\Theta }_j-ϵ,\dots ,{\Theta }_n)}{2ϵ}$

Octave 代码：

epsilon = 1e-4;
for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon);
end

在得出 gradApprox 梯度向量后，将其同之前计算的偏导 $D$ 比较，如果相等或很接近，即说明算法没有问题。

在确认算法没有问题后（一般只需运行一次），由于数值估计的梯度检验效率很低，所以一定要禁用它。

9.6 随机初始化（Random Initialization）

逻辑回归中，初始参数向量全为 0 没什么问题，在神经网络中，情况就不一样了。

初始权重如果全为 0，忆及 $z^{(l)}={\Theta }^{(l-1)}{a}^{(l-1)}$，则隐藏层除了偏置单元，都为 0，而每个单元求导的值也都一样，这就相当于是在不断重复计算同一结果，也就是算着算着，一堆特征在每一层都变成只有一个特征（虽然有很多单元，但值都相等），这样，神经网络的性能和效果都会大打折扣，故需要随机初始化初始权重。

随机初始化权重矩阵也为实现细节之一，用于打破对称性（Symmetry Breaking），使得 ${\Theta }_{ij}^{(l)}\in [-ϵ,ϵ]$ 。

Octave 代码：

当然，初始权重的波动也不能太大，一般限定在极小值 $ϵ$ 范围内，即 ${\Theta }_{i,j}^{(l)}\in [-ϵ,ϵ]$。

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

rand(m,n): 返回一个在区间 $(0,1)$ 内均匀分布的随机矩阵。

$ϵ$: 和梯度下降中的 $ϵ$ 没有联系，这里只是一个任意实数，给定了权重矩阵初始化值的范围。

9.7 综合起来（Putting It Together）

一般来说，应用神经网络有如下步骤：

1. 神经网络的建模（后续补充）

   • 选取特征，确定特征向量 $x$ 的维度，即输入单元的数量。
   • 鉴别分类，确定预测向量 $h_{\Theta }(x)$ 的维度，即输出单元的数量。
   • 确定隐藏层有几层以及每层隐藏层有多少个隐藏单元。

   默认情况下，隐藏层至少要有一层，也可以有多层，层数越多一般意味着效果越好，计算量越大。

2. 训练神经网络

   1. 随机初始化初始权重矩阵

   2. 应用前向传播算法计算初始预测

   3. 计算代价函数 $J(\Theta )$ 的值

   4. 应用后向传播宣发计算 $J(\Theta )$ 的偏导数

   5. 使用梯度检验检查算法的正确性，别忘了用完就禁用它

   6. 丢给最优化函数最小化代价函数

      由于神经网络的代价函数非凸，最优化时不一定会收敛在全局最小值处，高级最优化函数能确保收敛在某个局部最小值处。

9.8 自主驾驶（Autonomous Driving）

描述了神经网络在于自动驾驶领域的应用实例，用于打鸡血，笔记略。