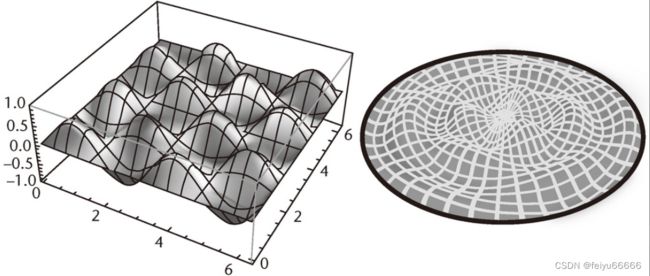
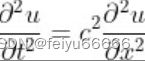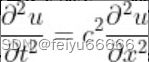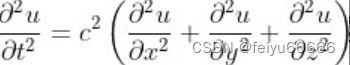伊恩·斯图尔特《改变世界的17个方程》波动方程笔记

主要是课堂的补充（yysy，我觉得课堂的教育模式真有够无聊的，PPT、写作业、考试，感受不到知识的魅力。

它告诉我们什么？

小提琴琴弦上某个小段的加速度，与相邻段相对于该段的平均位移成正比。

为什么重要？

它预测弦将会呈波浪般运动，并且它自然地推广到其他会出现波的物理系统。

它带来了什么？

我们对水波、声波、光波、弹性振动等的理解有了一个飞跃…… 地震学家使用它的改进版本，由地球的振动方式推断其内部结构。石油公司使用类似的方法寻找石油。在第11章中，我们将看到它如何预测电磁波的存在，从而带来了无线电、电视、雷达和现代通信。

从弦乐说起

毕达哥拉斯学派

毕达哥拉斯世界观的重大成就之一来自音乐。流传的故事五花八门，其中一篇说毕达哥拉斯经过一家铁匠铺，他注意到不同大小的锤子发出不同音高的声音，而有简单数字关系的锤子（例如一个锤子是另一个的两倍大）发出了和谐的声音。虽然这个故事很有趣，但任何实际用真的锤子试过的人都会发现，铁匠的操作并不特别具有音乐性，而且锤子的形状太复杂，不能和谐地振动。但是其中还是有一点儿道理的：总的来说，小的物体比大的物体产生的音调更高。

在提到毕达哥拉斯学派使用张紧的弦（一种称为卡龙琴的简单乐器）进行的一系列实验时，这些故事就变得更加可信了。我们之所以知道这些实验，是因为托勒密于公元150年左右在他的《谐和论》中提到了它们。通过将支撑物移动到琴弦上的各个位置，毕达哥拉斯学派发现，当两根张力相等的弦的长度成简单比例，例如2:1或3:2时，它们会产生异常和谐的音符。

乐理

音乐家利用“音程”来描述成对的音符，它衡量的是某种音阶中两个音相距几度。最基本的音程是八度，即钢琴上跨越八个白键的音。注意，除了一个音比另一个高之外，相距八度的音听起来非常相似，它们非常和谐。事实上，基于八度音阶的和声可能听起来有点儿乏味。在小提琴上，要演奏比空弦高一个八度的音，方法是将琴弦的中点压在指板上。弦长缩短一半，音就高一个八度。因此，八度音程对应的是简单的2:1数值比。

其他和谐音程也对应着简单的数值比。西方音乐中最重要的是四度，比例为4:3；还有五度，比例为3:2。如果考虑C D E F G A B C的音阶，这些音程的名字就说得通了。以C为根音，对应的四度的音符是F，五度是G，八度是C。如果我们将音符连续编号，根音为1，那么这些音就对应音阶上的第4、第5和第8个音符。几何关系在吉他这样的乐器上特别清晰，它在不同的相对位置上安装了金属条，也就是“品格”。四度的品格就在弦长的四分之一处，五度是三分之一处，八度是中点处。你可以用卷尺来检查一下。

这些比例为音阶提供了理论基础，并得出了如今大多数西方音乐中使用的音阶。这个故事很复杂，所以我会给出一个简化的版本。为了下文的方便，我从现在开始会把比例3:2写成分数。从根音开始，每升高五度，就可以得到一系列弦长

 计算出这些分数的乘方，就变成

除了前两个音符之外，其他这些音符都太高了，没法保持在八度音程内，但我们可以反复将分数除以2，来把它们降低一个或多个八度，直到结果落在1和2之间。把它们按升序排列，这就得到了分数

这些比例与钢琴上的C D E G A B音符非常接近。请注意，没有F。事实上，在人耳中，和之间的距离听起来比其他音程要大。为了填补这个空白，我们插入，即四度的比例，这与钢琴上的F非常接近。用高八度、比例为2的第二个C来补齐这套音阶也很好。现在我们就完全基于四度、五度和八度得到了一套音阶，各个音的比例如下：

长度与音高成反比，因此我们必须把分数颠倒才能得到相应的长度。

我们现在已经解释了钢琴上所有白键的音，但还有黑键的音。它们之所以会出现，是因为音阶中挨着的两个音之间具有两种不同的比例：（全音）和（半音）。例如，与的比例是，而与的比例是。“全音”和“半音”表示的是音程的近似比较。对应的比例数字分别是1.125和1.05。第一个比例更大，所以全音对应的音调变化比半音更大。两个半音构成的比例是，约为1.11，距离1.25不远。所以两个半音接近一个全音。我承认，不是很接近。

继续这样做下去的话，我们可以将每个全音分成两个音程，每个音程都接近一个半音，从而得到12音的音阶。这有几种不同做法，可以得到些微不同的结果。不管怎么做，当改变乐曲的调号时，都可能出现细微但可以听到的问题：如果我们将每个音符向上移动半音，则音程会略有改变。如果我们把半音定为一个特定比例，令其12次幂等于2，则可以避免这种效应。这样一来，两个半音就可以精确地构成一个全音，而12个半音将形成一个八度，你可以通过向上或向下移动所有音符来改变音阶。

批注：现在你已经知道对应关系了，请制作一把乐器吧。

牛顿定律的运用

伯努利的研究

关键在于将加速度与力联系起来的牛顿第二运动定律。你还需要知道，随着弦的运动，也就是轻微地拉伸或收缩时，张紧的弦的拉力如何变化。为此，我们要使用牛顿那个不情不愿的对手胡克于1660年发现的东西，它称为胡克定律：弹簧长度的变化与施加给它的力成正比。（小提琴琴弦实际上相当于一种弹簧，所以适用相同的法则。）还有一个障碍。我们可以将牛顿定律应用于由有限个质点组成的系统：我们为每个质点列出一个方程，然后尽力解出最终得到的方程组。但是小提琴琴弦是一个连续体，一条由无限多个点组成的线。因此，当时的数学家把弦看成大量排列紧密的质点，由遵循胡克定律的弹簧连接在一起。他们写下了方程，略微简化以使它们可解；然后解出了方程；最后，他们让质点的数量变得任意大，并搞清楚解会有什么变化。

批注：那么形变量是怎么考虑的？

约翰·伯努利在1727年实施了这个计划，如果想想有多少困难被隐藏了起来，这个结果算得上非常漂亮。为了避免在下面的描述中出现混淆，想象把小提琴平放，弦是水平的。拨弦时，弦会在与小提琴垂直的方向上下振动。这是你要记住的一个情景。用弓拉弦会导致弦侧向振动，而且弓的存在也十分麻烦。在数学模型中，没有小提琴，只有一根弦，两端固定；弦在平面内上下振动。

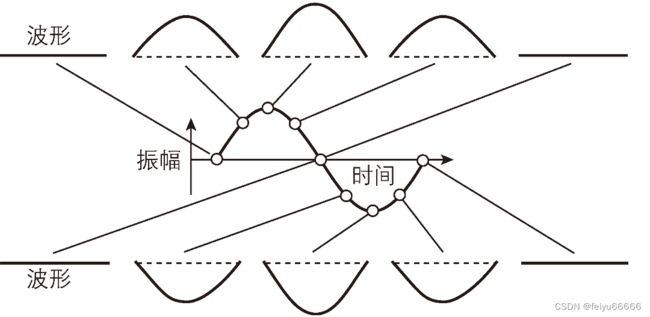
在这个情景中，伯努利发现，在任何时刻，振动中的弦的形状都是正弦曲线。振动的幅度（曲线的最大高度）也遵循正弦曲线，不过是随时间而不是随空间变化的正弦曲线。用符号表示的话，他的解形如，其中c是常数，如图所示。空间项告诉我们形状，但它在t时刻要缩放的倍数是因子。这个式子表示琴弦上下振动，一遍又一遍地重复相同的动作。振荡周期，也就是连续两次重复之间的时间，是。

批注：反正我觉得比上课讲得好，md，上课就是PPT+做题，无语了。

 这是伯努利得到的最简单的解，但还有其他解；所有解都是正弦曲线，也就是不同的振动“模态”，指的是沿着弦的长度方向有1、2、3或更多个波浪，如下图所示。同样，任何时刻形状的快照都是正弦曲线，振幅要乘上一个和时间相关的因子，而这个因子也是正弦变化的。公式是，……依此类推。

波动方程

如果我们将伯努利的方法用于方程而不是解，那么根据牛顿第二运动定律就可以得到波动方程。1746年，让·勒朗·达朗贝尔(Jean Le Rond d'Alembert)遵循标准步骤，将振动的小提琴琴弦作为质点的集合处理，但是当质点数趋于无穷大时，他没有求解方程并寻找模态，而是研究了方程本身发生了什么。他推导出了一个方程，描述了弦的形状随时间的变化。但在我向你展示它是什么样之前，我们需要一个新的思想，称为“偏导数”。

偏导数的概念

想象一下自己在大海中央，看着各种形状和大小的波浪经过。当波浪经过时，你会上下晃动。在物理上，你可以通过几种不同的方式描述周围环境的变化。特别是，你可以专注于时间的变化或空间的变化。随着时间的推移，在你的位置上，高度随着时间变化的速率就是高度对时间的导数。

但这并没有描述你附近海洋的形状，只描述了经过你身下的波浪有多高。要描述形状，你可以（从概念上）冻结时间并计算波浪的高度：不仅是在你的位置，还包括附近的位置。然后就可以使用微积分来计算波浪在你所在位置的倾斜程度。你是处于高峰或低谷吗？如果是的话，则斜率为零。你是在波浪的一半之处吗？如果是的话，则斜率非常大。用微积分的话来说，你可以通过计算波的高度对空间的导数来求出这个斜率的值。

如果函数仅依赖于一个变量（称之为），我们将导数写为：的微小变化除以的微小变化。但是就海浪而言，函数（波高）不仅取决于空间，还取决于时间。在任何给定时刻，我们仍然可以计算出；它告诉我们波浪的局部斜率。但我们可以固定时间让空间变化，也可以固定空间让时间变化，这告诉我们上下摆动的速度。我们可以使用符号来表示这个“时间导数”，并将其解释为“的微小变化除以的微小变化”。但是这种记法隐藏了一个模糊的地方：在这两种情况下，高度的微小变化可能并且通常是不同的。如果你忘了这一点，计算就可能出错。当我们对空间微分时，是让空间变量稍微改变，看看高度如何变化；当我们对时间微分时，则是让时间变量稍微改变，看看高度如何变化。随时间的变化没有理由非要等于随空间的变化。

因此，数学家决定把符号改成一种不会（直接）让他们想到是“微小变化”的东西，以此提醒自己注意这种模糊的问题。他们选择了一个非常可爱的花体的，写作；然后把这两种导数分别写作和。你可能会说，这并不是一个很大的进步，因为两种不同的含义还是一样容易混淆。对这种批评有两个回应：其一是在这种情况下，你不应该认为是的特定微小变化；其二是使用花哨的新符号提醒你不要混淆。第二个回应肯定是有效的：只要你看到，它就会告诉你，你会看到相对于几个不同变量的变化率。这些变化率称为偏导数，因为从概念上讲，你只让部分变量变化，而让其余变量保持不变。

批注：看来我学的是真有够烂的（捂脸）。

回到达朗贝尔

当达朗贝尔计算出振动弦的方程时，他就恰恰遇到了这种情况。弦的形状取决于空间（沿着弦的距离）以及时间。牛顿第二运动定律告诉他，一小段弦的加速度与作用于它的力成正比。加速度是对时间的（二阶）导数。但是力是由相邻的弦段作用于我们研究的弦产生的，而“相邻”意味着空间的微小变化。当他计算这些力时，就得出了方程

其中u(x,t)是t时刻弦上x位置处的垂直位置，c是与弦的张力以及弹性大小有关的常数。这个计算实际上比伯努利所做的更容易，因为它避免了引入特解带来的特殊性质。达朗贝尔优雅的公式就是波动方程。和牛顿第二运动定律一样，它是一个微分方程——涉及u的（二阶）导数。由于它们是偏导数，因此波动方程是偏微分方程。空间二阶导数表示作用在弦上的净力，而时间二阶导数是加速度。波动方程开创了一个先例：经典数学物理学中的大多数关键方程，以及许多现代数学物理方程，是偏微分方程。

批注：推导见下。

达朗贝尔一写下波动方程，就做好了把它解出来的准备。这项任务因为它是一个线性方程而变得很容易。偏微分方程有许多解（通常是无限多组解），因为每个初始状态都会导致一个不同的解。例如，小提琴琴弦原则上可以在释放之前弯曲成你喜欢的任何形状，然后由波动方程接管。“线性”意味着如果u(x,t)和v(x,t)是解，则任何线性组合au(x,t)+bv(x,t)也是解，其中a和b是常数。另一个术语是“叠加”。波动方程的线性来源于伯努利和达朗贝尔必须做出的近似——这样才能得到他们可以解的东西：假设所有干扰都很小。现在，弦施加的力可以用各个质点位移的线性组合来良好地近似。更好的近似将得出非线性偏微分方程，那可就麻烦得多了。从长远来看，这些复杂性必须被正面解决，但先驱们已经有足够的东西要对付了，所以他们选择了近似但非常优雅的方程，并将注意力限制在振幅很小的波上。这个方法很好用。事实上，对于振幅较大的波，它通常也很好用，这是一个幸运的奖励。

批注：上课没讲过这个（上课只讲如何做题，笑麻了），，，

达朗贝尔知道自己的方向是正确的，因为他找到了固定的形状沿着弦线像波浪般行进的解。结果他发现，波速就是等式中的常数c。波可以向左或向右传播，于是叠加原理发挥了作用。达朗贝尔证明了所有解都是向左传播或向右传播的两个波的叠加。而且每个单独的波可以具有任何形状。在小提琴琴弦上看到的两端固定的驻波，其实是两列形状相同但颠倒的波的组合，一列向左传播，另一列（颠倒地）向右传播。两列波在末端处完全抵消：一列波的波峰与另一列波的波谷重合。因此它们符合物理边界条件。

批注：这周刚好讲的是这个，波的叠加，，，u(x,t)=f(x-ct)+g(x+ct)

数学家现在面临着一个过犹不及的窘境。波动方程有两种解法：伯努利的解法会得出正弦和余弦，而达朗贝尔的解法会得出任意形状的波。乍看起来，似乎达朗贝尔的解法肯定更加通用：正弦和余弦都是函数，但大多数函数不是正弦和余弦。然而波动方程是线性的，所以你可以将伯努利的解叠加在一起，也就是把解的常数倍加在一起。为了简单起见，我们只考虑某个固定时刻的快照，这样就不依赖于时间了。

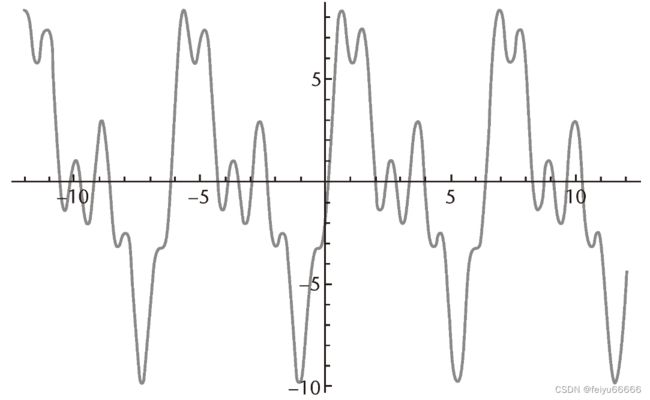
例如，下图是5sinx+4sin2x-2cos6x。这是一个相当不规则的形状，它扭来扭去，但仍然光滑并呈波浪状。

让那些思维更为缜密的数学家感到困扰的是，有些函数非常粗糙，如锯齿般参差不齐，你没有办法把它们表示成正弦和余弦的线性组合。好吧，如果你使用有限项的话是没办法——而这就指明了一条出路。正弦和余弦的无穷级数如果收敛（即无穷项之和是有意义的）也满足波动方程。它是不是能同时表达锯齿状的函数和平滑的函数呢？一流的数学家们就此进行了争论，在热学理论中出现同样的问题时终于有了头绪。关于热流的问题自然会涉及有突变的不连续函数，这比锯齿状的函数还要糟糕。我将在第9章讲述这个故事，但最终结果是，大多数“合理的”波形可以用正弦和余弦的无穷级数来表示，也就是可以通过正弦和余弦的有限组合无限近似。

批注：傅里叶变换吧。

波动方程的推导

考虑三个连续的质点，编号分别为n-1、n、n+1。假设在t时刻，它们相对于水平轴上的初始位置的位移分别是、和。根据牛顿第二运动定律，每个质点的加速度与作用于它的力成正比。简化假设，设每个质点仅在垂直方向上移动很小的距离。那么一个很好的近似是，质点n-1施加在质点n上的力与差值成正比，类似地，质点n+1施加在质点n上的力与差值成正比。将这些全都加在一起，施加在质点n上的总力与成正比。这就是这条式子上面两条式子之差，因此，对质点n施加的力是差值的差值。

现在假设质点非常紧密。在微积分中，差值——除以适当的小常数——是对导数的近似。差值的差值是对导数的导数的近似，即二阶导数。那么在质点数量趋于无穷大、质点之间距离趋于无穷小的极限，弦上某一点所受的力就与成正比，其中x是沿弦长度方向的空间坐标。根据牛顿第二运动定律，它与垂直于轴线方向的加速度成正比，也就是时间的二阶导数。将比例常数写作可得

三维空间的波动方程

数学家首先在他们能想到的最简单的条件下推导出了波动方程：一条振动的线，这是一个一维系统。现实中的应用需要更一般性的理论，在二维和三维中对波建模。即使只谈音乐领域，鼓也需要两个维度来模拟鼓皮振动的规律。海洋表面的水波也是如此。地震发生时，整个地球像钟声一样响起，而我们的星球是三维的。许多其他物理领域涉及二维或三维的模型。人们发现，将波动方程扩展到更高维度十分简单、直接，你所要做的就是重复类似于对小提琴琴弦的计算。学会在简单的条件下玩这个游戏之后，在真实环境中玩就不难了。

例如，在三维空间中，我们使用三个空间坐标(x,y,z)和时间t。波用函数u来描述，这个函数取决于这四个坐标。例如，它可以描述声波穿过空气时空气中的压力变化。利用和达朗贝尔相同的假设，特别是扰动的振幅很小，用同样的方法可得出同样漂亮的方程：

括号内的公式称为u的拉普拉斯算子，它对应于所讨论的点与其附近的点之间u值的平均差。这种表达在数学物理学中出现得如此频繁，以至于拥有了自己的特殊符号：。如果要得到二维拉普拉斯算子，我们只要略去涉及z的项就可以得出二维条件下的波动方程。

高维条件下出现的新东西主要在于发生波的区域（称为方程的定义域）可能很复杂。在一维条件下，唯一连通的形状是区间，也就是线段。然而，在二维情况下，它可以是你在平面中画出的任何形状；在三维情况下，它就可以是空间中的任何形状。你可以对方形鼓、矩形鼓、圆形鼓或轮廓像猫的鼓建模。对于地震，你可以使用球形定义域，或者为了得到更高精度，使用在极点处略微压扁的椭球体。如果你正在设计汽车并希望消除不必要的振动，那么定义域应该是汽车的形状，或者工程师想要关注的汽车的任何部分。

对于任何选定形状的定义域，都有类似于伯努利的正弦和余弦的函数——最简单的振动模式。这些模式被称为“模态”，或更为精确地说是“简正模”。所有其他波都可以通过简正模的叠加得到，而如果有必要的话，还可以再次使用无穷级数。简正模的频率表示定义域的自然振动频率。如果定义域是矩形，则这些函数是sinmxcosny形式的三角函数，其中m和n是整数，产生如下所示的波形。如果定义域是圆形，则由称为贝塞尔函数的新函数确定，具有更有趣的形状。由此产生的数学不仅适用于鼓，也适用于水波、声波、电磁波或光（见第11章）甚至量子波（见第14章）。这是所有这些领域的基础。拉普拉斯算子也出现在其他物理现象的方程中，特别是电场、磁场和引力场。“从玩具问题（一个如此简单以至于不可能符合现实的问题）入手”，这个数学家们最喜欢的技巧在波上取得了巨大的成功。

这就是不应该用一个数学概念最初出现时的背景来评判它的原因。如果你想要了解的是地震，那么对小提琴琴弦进行建模似乎毫无意义。但是如果你直接跳入深渊，并试图解决真实地震的所有复杂性，那你就会被淹死。你应该先开始在浅水区划水，培养在游泳池游几个来回的信心，然后你就可以做好准备爬上高高的跳板了。

对波动方程假设的完善

波动方程取得了辉煌的成功，在某些物理领域，它非常精确地描述了现实。但是，它的推导需要几个简化的假设。当这些假设不切实际时，可以修改相同的物理概念以适应条件，从而得出波动方程的不同版本。

地震就是一个典型的例子。这里的主要问题不在于达朗贝尔假设波动的振幅很小，而是在于定义域的物理性质起了变化。这些性质可以对地震波——通过地球传播的振动产生强烈的影响。通过了解这些效应，我们可以深入了解我们的星球，并搞清楚它是由什么组成的。

地震波有两种主要类型：压力波和剪切波，通常缩写为P波和S波（还有很多其他波：这是一个简化版本，只介绍一些基础知识）。两者都可以在固体介质中发生，但S波不会在流体中发生。P波是压力的波，类似于空气中的声波，压力变化的方向是沿着波传播的方向，我们把这种波叫作“纵波”。S波则是“横波”，压力变化方向与传播方向垂直，就像小提琴琴弦上的波一样。它们会导致固体发生剪切，其形变就类似一沓被侧向推动的扑克牌，牌与牌之间会相互滑动。流体的行为和一沓牌可不一样。

当地震发生时，它会产生两种波。P波传播速度更快，因此地表其他地方的地震学家会首先观察到它们。然后较慢的S波才会到达。1906年，英国地质学家理查德·奥尔德姆(Richard Oldham)利用这种差异，做出了关于地球内部的重大发现。粗略地说，地球有一个铁芯，周围是岩石地幔，大陆漂浮在地幔顶部。奥尔德姆认为地核的外层必须是液体。如果是这样，S波不能通过这些区域，但P波可以。所以有所谓的S波阴影区，你可以通过观察地震信号来计算出它的位置。英国数学家哈罗德·杰弗里斯(Harold Jeffreys)在1926年对细节进行了整理，并确认奥尔德姆是正确的。

如果地震足够强烈，它可能导致整个地球以其一种简正模振动——类似于琴弦上的正弦和余弦。整个地球像钟声一样响起，在某种意义上说，如果我们真能听到它极低的频率的话，这甚至都不是一个比喻。能够记录这些模式的仪器出现在20世纪60年代，它们被用于观察有科学记载的两次最猛烈的地震：1960年的智利地震（9.5级）和1964年的阿拉斯加地震（9.2级）。第一次地震造成了约5000人死亡，第二次地震由于发生在偏远地区，造成了约130人死亡。两次地震都引发了海啸并造成了巨大的破坏。通过激发地球的基本振动模式，两次地震都前所未有地让我们了解到了地球的内部深处。

波动方程的复杂版本使地震学家能够看到我们脚下数百千米处发生的事情。他们可以绘出地球的一个构造板块滑动到另一个板块之下的情况，称为“俯冲”。俯冲作用会导致地震，尤其是所谓的“大型逆冲区地震”，就像前面提到的两次地震一样。它还会产生安第斯山等沿着大陆边缘的山脉，以及火山——板块下沉得如此之深以至于开始融化，导致岩浆上升到地表。最近的一个发现是，板块不需要作为一个整体隐没，而是可以分解成巨大的岩板，沉入地幔的不同深度。

这个领域最有价值的东西，就是可靠地预测地震和火山爆发的方法。地震和火山难以捉摸，因为触发此类事件的条件是许多地点的许多因素的复杂组合。然而研究有所进展，而地震学家使用的波动方程描述是许多正在被研究的方法的基石。