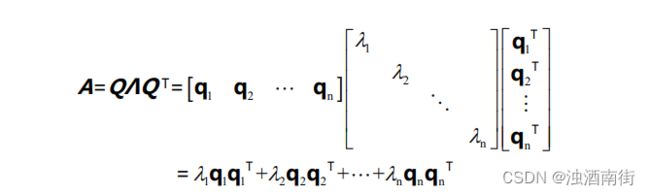- 日更006 终极训练营day3
懒cici
人生创业课(2)今天的主题:学习方法一:遇到有用的书,反复读,然后结合自身实际,列践行清单,不要再写读书笔记思考这本书与我有什么关系,我在哪些地方能用到,之后我该怎么用方法二:读完书没映像怎么办?训练你的大脑,方法:每读完一遍书,立马合上书,做一场分享,几分钟都行对自己的学习要求太低,要逼自己方法三:学习深度不够怎么办?找到细分领域的榜样,把他们的文章、书籍、产品都体验一遍,成为他们的超级用户,向
- 力扣热题100-------54. 螺旋矩阵
海航Java之路
力扣leetcode矩阵java
给你一个m行n列的矩阵matrix,请按照顺时针螺旋顺序,返回矩阵中的所有元素。示例1:输入:matrix=[[1,2,3],[4,5,6],[7,8,9]]输出:[1,2,3,6,9,8,7,4,5]示例2:输入:matrix=[[1,2,3,4],[5,6,7,8],[9,10,11,12]]输出:[1,2,3,4,8,12,11,10,9,5,6,7]提示:m==matrix.lengthn
- 48. 旋转图像 - 力扣(LeetCode)
Fiee-77
#数组leetcode算法python数据结构数组
题目:给定一个n×n的二维矩阵matrix表示一个图像。请你将图像顺时针旋转90度。你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。示例1:输入:matrix=[[1,2,3],[4,5,6],[7,8,9]]输出:[[7,4,1],[8,5,2],[9,6,3]]示例2:输入:matrix=[[5,1,9,11],[2,4,8,10],[13,3,6,
- 力扣面试题07 - 旋转矩阵
茶猫_
leetcode矩阵算法c语言
题目:给你一幅由N×N矩阵表示的图像,其中每个像素的大小为4字节。请你设计一种算法,将图像旋转90度。不占用额外内存空间能否做到?示例1:给定matrix=[[1,2,3],[4,5,6],[7,8,9]],原地旋转输入矩阵,使其变为:[[7,4,1],[8,5,2],[9,6,3]]示例2:给定matrix=[[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,
- 【花了N长时间读《过犹不及》,不断练习,可以越通透】
君君Love
我已经记不清花了多长时间去读《过犹不及》,读书笔记都写了42页,这算是读得特别精细的了。是一本难得的好书,虽然书中很多内容和圣经吻合,我不是基督徒,却觉得这样的文字值得细细品味,和我们的生活息息相关。我是个界线建立不牢固的人,常常愧疚,常常害怕他人的愤怒,常常不懂拒绝,还有很多时候表达不了自己真实的感受,心里在说不嘴里却在说好……这本书给我很多的启示,让我学会了怎样去建立属于自己的清晰的界限。建立
- 基于redis的Zset实现作者的轻量级排名
周童學
Javaredis数据库缓存
基于redis的Zset实现轻量级作者排名系统在今天的技术架构中,Redis是一种广泛使用的内存数据存储系统,尤其在需要高效检索和排序的场景中表现优异。在本篇博客中,我们将深入探讨如何使用Redis的有序集合(ZSet)构建一个高效的笔记排行榜系统,并提供相关代码示例和详细的解析。1.功能背景与需求假设我们有一个笔记分享平台,用户可以发布各种笔记,系统需要根据用户发布的笔记数量来生成一个实时更新的
- 常规笔记本和加固笔记本的区别
luchengtech
电脑三防笔记本加固计算机加固笔记本
在现代科技产品中,笔记本电脑因其便携性和功能性被广泛应用。根据使用场景和需求的不同,笔记本可分为常规笔记本和加固笔记本,二者在多个方面存在显著区别。适用场景是区分二者的重要标志。常规笔记本主要面向普通消费者和办公人群,适用于家庭娱乐、日常办公、学生学习等相对稳定的室内环境。比如,人们在家用它追剧、处理文档,学生在教室用它完成作业。而加固笔记本则专为特殊行业设计,像军事、野外勘探、工业制造、交通运输
- 第八课: 写作出版你最关心的出书流程和市场分析(无戒学堂复盘)
人在陌上
今天是周六,恰是圣诞节。推掉了两个需要凑腿的牌局,在一个手机,一个笔记本,一台电脑,一杯热茶的陪伴下,一个人静静地回听无戒学堂的最后一堂课。感谢这一个月,让自己的习惯开始改变,至少,可以静坐一个下午而不觉得乏味枯燥难受了,要为自己点个赞。我深知,这最后一堂课的内容,以我的资质和毅力,可能永远都用不上。但很明显,无戒学堂是用了心的,毕竟,有很多优秀学员,已经具备了写作能力,马上就要用到这堂课的内容。
- python笔记14介绍几个魔法方法
抢公主的大魔王
pythonpython
python笔记14介绍几个魔法方法先声明一下各位大佬,这是我的笔记。如有错误,恳请指正。另外,感谢您的观看,谢谢啦!(1).__doc__输出对应的函数,类的说明文档print(print.__doc__)print(value,...,sep='',end='\n',file=sys.stdout,flush=False)Printsthevaluestoastream,ortosys.std
- 《感官品牌》读书笔记 1
西红柿阿达
原文:最近我在东京街头闲逛时,与一位女士擦肩而过,我发现她的香水味似曾相识。“哗”的一下,记亿和情感立刻像潮水般涌了出来。这个香水味把我带回了15年前上高中的时候,我的一位亲密好友也是用这款香水。一瞬间,我呆站在那里,东京的街景逐渐淡出,取而代之的是我年少时的丹麦以及喜悦、悲伤、恐惧、困惑的记忆。我被这熟悉的香水味征服了。感想:感官是有记忆的,你所听到,看到,闻到过的有代表性的事件都会在大脑中深深
- 我不想再当知识的搬运工
楚煜楚尧
因为学校课题研究的需要,这个暑假我依然需要完成一本书的阅读笔记。我选的是管建刚老师的《习课堂十讲》。这本书,之前我读过,所以重读的时候,感到很亲切,摘抄起来更是非常得心应手。20页,40面,抄了十天,终于在今天大功告成了。这对之前什么事都要一拖再拖的我来说,是破天荒的改变。我发现至从认识小尘老师以后,我的确发生了很大的改变。遇到必须做却总是犹豫不去做的事,我学会了按照小尘老师说的那样,在心里默默数
- 机器学习必备数学与编程指南:从入门到精通
a小胡哦
机器学习基础机器学习人工智能
一、机器学习核心数学基础1.线性代数(神经网络的基础)必须掌握:矩阵运算(乘法、转置、逆)向量空间与线性变换特征值分解与奇异值分解(SVD)为什么重要:神经网络本质就是矩阵运算学习技巧:用NumPy实际操作矩阵运算2.概率与统计(模型评估的关键)核心概念:条件概率与贝叶斯定理概率分布(正态、泊松、伯努利)假设检验与p值应用场景:朴素贝叶斯、A/B测试3.微积分(优化算法的基础)重点掌握:导数与偏导
- 20210517坚持分享53天读书摘抄笔记 非暴力沟通——爱自己
f79a6556cb19
让生命之花绽放在赫布·加德纳(HerbGardner)编写的《一千个小丑》一剧中,主人公拒绝将他12岁的外甥交给儿童福利院。他郑重地说道:“我希望他准确无误地知道他是多么特殊的生命,要不,他在成长的过程中将会忽视这一点。我希望他保持清醒,并看到各种奇妙的可能。我希望他知道,一旦有机会,排除万难给世界一点触动是值得的。我还希望他知道为什么他是一个人,而不是一张椅子。”然而,一旦负面的自我评价使我们看
- Unity学习笔记1
zy_777
通过一个星期的简单学习,初步了解了下unity,unity的使用,以及场景的布局,UI,以及用C#做一些简单的逻辑。好记性不如烂笔头,一些关键帧还是记起来比较好,哈哈,不然可能转瞬即逝了,(PS:纯小白观点,unity大神可以直接忽略了)一:MonoBehaviour类的初始化1,Instantiate()创建GameObject2,通过Awake()和Start()来做初始化3,Update、L
- 大数据技术笔记—spring入门
卿卿老祖
篇一spring介绍spring.io官网快速开始Aop面向切面编程,可以任何位置,并且可以细致到方法上连接框架与框架Spring就是IOCAOP思想有效的组织中间层对象一般都是切入service层spring组成前后端分离已学方式,前后台未分离:Spring的远程通信:明日更新创建第一个spring项目来源:科多大数据
- Django学习笔记(一)
学习视频为:pythondjangoweb框架开发入门全套视频教程一、安装pipinstalldjango==****检查是否安装成功django.get_version()二、django新建项目操作1、新建一个项目django-adminstartprojectproject_name2、新建APPcdproject_namedjango-adminstartappApp注:一个project
- python学习笔记(汇总)
朕的剑还未配妥
python学习笔记整理python学习开发语言
文章目录一.基础知识二.python中的数据类型三.运算符四.程序的控制结构五.列表六.字典七.元组八.集合九.字符串十.函数十一.解决bug一.基础知识print函数字符串要加引号,数字可不加引号,如print(123.4)print('小谢')print("洛天依")还可输入表达式,如print(1+3)如果使用三引号,print打印的内容可不在同一行print("line1line2line
- 顺时针旋转N * N 的矩阵
忆杰
算法Python矩阵python算法
顺时针旋转题目描述数据范围实现逻辑代码实现题目描述有一个NxN整数矩阵,请编写一个算法,将矩阵顺时针旋转90度。给定一个NxN的矩阵,和矩阵的阶数N,请返回旋转后的NxN矩阵。数据范围0852789963'''#第N列逆序后变成第N行#或者是第i行变成第N-i-1列代码实现classSolution:#列转换为行defline2Row(self,mat,n):arr=[]forlineinrang
- Redis 分布式锁深度解析:过期时间与自动续期机制
爱恨交织围巾
分布式事务redis分布式数据库微服务学习go
Redis分布式锁深度解析:过期时间与自动续期机制在分布式系统中,Redis分布式锁的可靠性很大程度上依赖于对锁生命周期的管理。上一篇文章我们探讨了分布式锁的基本原理,今天我们将聚焦于一个关键话题:如何通过合理设置过期时间和实现自动续期机制,来解决分布式锁中的死锁与锁提前释放问题。一、为什么过期时间是分布式锁的生命线?你的笔记中提到"服务挂掉时未删除锁可能导致死锁",这正是过期时间要解决的核心问题
- 08.学习闭环三部曲:预习、实时学习、复习
0058b195f4dc
人生就是一本效率手册,你怎样对待时间,时间就会给你同比例的回馈。单点突破法。预习,实时学习,复习。1、预习:凡事提前【计划】(1)前一晚设置三个当日目标。每周起始于每周日。(2)提前学习。预习法进行思考。预不预习效果相差20%,预习法学会提问。(3)《学会提问》。听电子书。2.实时学习(1)(10%)相应场景,思维导图,快速笔记。灵感笔记。(2)大纲,基本记录,总结篇。3.复习法则,(70%),最
- 《如何写作》文心读书笔记
逆熵反弹力
《文心》这本书的文体是以讲故事的形式来讲解如何写作的,读起来不会觉得刻板。读完全书惊叹大师的文笔如此之好,同时感叹与此书相见恨晚。工作了几年发现表达能力在生活中越来越重要,不管是口语还是文字上的表达。有时候甚至都不能把自己想说的东西表达清楚,平时也有找过一些书来看,想通过提升自己的阅读量来提高表达能力。但是看了这么久的书发现见效甚微,这使得我不得不去反思,该怎么提高表达能力。因此打算从写作入手。刚
- SQL笔记纯干货
AI入门修炼
oracle数据库sql
软件:DataGrip2023.2.3,phpstudy_pro,MySQL8.0.12目录1.DDL语句(数据定义语句)1.1数据库操作语言1.2数据表操作语言2.DML语句(数据操作语言)2.1增删改2.2题2.3备份表3.DQL语句(数据查询语言)3.1查询操作3.2题一3.3题二4.多表详解4.1一对多4.2多对多5.多表查询6.窗口函数7.拓展:upsert8.sql注入攻击演示9.拆表
- 《4D卓越团队》习书笔记 第十六章 创造力与投入
Smiledmx
《4D卓越团队-美国宇航局的管理法则》(查理·佩勒林)习书笔记第十六章创造力与投入本章要点:务实的乐观不是盲目乐观,而是带来希望的乐观。用真相激起希望吉姆·科林斯在《从优秀到卓越》中写道:“面对残酷的现实,平庸的公司选择解释和逃避,而不是正视。”创造你想要的项目1.你必须从基于真相的事实出发。正视真相很难,逃避是人类的本性。2.面对现实,你想创造什么?-我想利用现有资源创造一支精干、高效、积极的橙
- 2020-12-10
生活有鱼_727f
今日汇总:1.学习了一只舞蹈2.专业知识抄了一遍3.讲师训作业完成今日不足之处:1.时间没管理好,浪费了很多时间到现在才做完明日必做:1.讲师训作业完成2.群消息做好笔记3.宽带安装
- 【Druid】学习笔记
fixAllenSun
学习笔记oracle
【Druid】学习笔记【一】简介【1】简介【2】数据库连接池(1)能解决的问题(2)使用数据库连接池的好处【3】监控(1)监控信息采集的StatFilter(2)监控不影响性能(3)SQL参数化合并监控(4)执行次数、返回行数、更新行数和并发监控(5)慢查监控(6)Exception监控(7)区间分布(8)内置监控DEMO【4】Druid基本配置参数介绍【5】Druid相比于其他数据库连接池的优点
- 微信公众号写作:如何通过文字变现?
氧惠爱高省
微信公众号已成为许多人分享知识、表达观点的重要平台。随着自媒体的发展,越来越多的人开始关注微信公众号上写文章如何挣钱的问题。本文将详细探讨微信公众号写作的盈利模式,帮助广大写作者实现文字变现的梦想。公众号流量主就找善士导师(shanshi2024)公众号:「善士笔记」主理人,《我的亲身经历,四个月公众号流量主从0到日入过万!》公司旗下管理800+公众号矩阵账号。代表案例如:爸妈领域、职场道道、国学
- 在奋斗的年华里,怎么让你的一年顶别人的十年呢丨看看剽悍一只猫
十里荷塘秋水长
“剽悍一只猫”在自媒体时代是传奇之一,据说这个人让自己从一无所有的普通人到现在的网络江湖的传奇人物也没有用太长的时间,但是人家现在是樊登读书首席社群顾问、社群商业战略专家、个人成长战略深度研究者&践行者。他自己的微信公众号矩阵有百万读者。早早就借助于互联网的力量实现了财务自由。很多人希望能取经咨询,但是老师的时间极其宝贵高效,一般个人的咨询没有办法安排时间接,再加上收费也不好控制,高了低了对口碑来
- 流利说懂你英语笔记要点句型·核心课·Level 8·Unit 3·Part 2·Video 1·Healing Architecture 1
羲之大鹅video
HealingArchitecture1EveryweekendforaslongasIcanremember,myfatherwouldgetuponaSaturday,putonawornsweatshirtandhe'dscrapeawayatthesqueakyoldwheelofahousethatwelivedin.ps:从我记事起,每个周末,我父亲都会在周六起床,穿上一件破旧的运动衫
- java学习笔记8
幸福,你等等我
学习笔记java
一、异常处理Error:错误,程序员无法处理,如OOM内存溢出错误、内存泄漏...会导出程序崩溃1.异常:程序中一些程序自身处理不了的特殊情况2.异常类Exception3.异常的分类:(1).检查型异常(编译异常):在编译时就会抛出的异常(代码上会报错),需要在代码中编写处理方式(和程序之外的资源访问)直接继承Exception(2).运行时异常:在代码运行阶段可能会出现的异常,可以不用明文处理
- 2025.07 Java入门笔记01
殷浩焕
笔记
一、熟悉IDEA和Java语法(一)LiuCourseJavaOOP1.一直在用C++开发,python也用了些,Java是真的不熟,用什么IDE还是问的同事;2.一开始安装了jdk-23,拿VSCode当编辑器,在cmd窗口编译运行,也能玩;但是想正儿八经搞项目开发,还是需要IDE;3.安装了IDEA社区版:(1)IDE通常自带对应编程语言的安装包,例如IDEA自带jbr-21(和jdk是不同的
- Spring4.1新特性——Spring MVC增强
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- mysql 性能查询优化
annan211
javasql优化mysql应用服务器
1 时间到底花在哪了?
mysql在执行查询的时候需要执行一系列的子任务,这些子任务包含了整个查询周期最重要的阶段,这其中包含了大量为了
检索数据列到存储引擎的调用以及调用后的数据处理,包括排序、分组等。在完成这些任务的时候,查询需要在不同的地方
花费时间,包括网络、cpu计算、生成统计信息和执行计划、锁等待等。尤其是向底层存储引擎检索数据的调用操作。这些调用需要在内存操
- windows系统配置
cherishLC
windows
删除Hiberfil.sys :使用命令powercfg -h off 关闭休眠功能即可:
http://jingyan.baidu.com/article/f3ad7d0fc0992e09c2345b51.html
类似的还有pagefile.sys
msconfig 配置启动项
shutdown 定时关机
ipconfig 查看网络配置
ipconfig /flushdns
- 人体的排毒时间
Array_06
工作
========================
|| 人体的排毒时间是什么时候?||
========================
转载于:
http://zhidao.baidu.com/link?url=ibaGlicVslAQhVdWWVevU4TMjhiKaNBWCpZ1NS6igCQ78EkNJZFsEjCjl3T5EdXU9SaPg04bh8MbY1bR
- ZooKeeper
cugfy
zookeeper
Zookeeper是一个高性能,分布式的,开源分布式应用协调服务。它提供了简单原始的功能,分布式应用可以基于它实现更高级的服务,比如同步, 配置管理,集群管理,名空间。它被设计为易于编程,使用文件系统目录树作为数据模型。服务端跑在java上,提供java和C的客户端API。 Zookeeper是Google的Chubby一个开源的实现,是高有效和可靠的协同工作系统,Zookeeper能够用来lea
- 网络爬虫的乱码处理
随意而生
爬虫网络
下边简单总结下关于网络爬虫的乱码处理。注意,这里不仅是中文乱码,还包括一些如日文、韩文 、俄文、藏文之类的乱码处理,因为他们的解决方式 是一致的,故在此统一说明。 网络爬虫,有两种选择,一是选择nutch、hetriex,二是自写爬虫,两者在处理乱码时,原理是一致的,但前者处理乱码时,要看懂源码后进行修改才可以,所以要废劲一些;而后者更自由方便,可以在编码处理
- Xcode常用快捷键
张亚雄
xcode
一、总结的常用命令:
隐藏xcode command+h
退出xcode command+q
关闭窗口 command+w
关闭所有窗口 command+option+w
关闭当前
- mongoDB索引操作
adminjun
mongodb索引
一、索引基础: MongoDB的索引几乎与传统的关系型数据库一模一样,这其中也包括一些基本的优化技巧。下面是创建索引的命令: > db.test.ensureIndex({"username":1}) 可以通过下面的名称查看索引是否已经成功建立: &nbs
- 成都软件园实习那些话
aijuans
成都 软件园 实习
无聊之中,翻了一下日志,发现上一篇经历是很久以前的事了,悔过~~
断断续续离开了学校快一年了,习惯了那里一天天的幼稚、成长的环境,到这里有点与世隔绝的感觉。不过还好,那是刚到这里时的想法,现在感觉在这挺好,不管怎么样,最要感谢的还是老师能给这么好的一次催化成长的机会,在这里确实看到了好多好多能想到或想不到的东西。
都说在外面和学校相比最明显的差距就是与人相处比较困难,因为在外面每个人都
- Linux下FTP服务器安装及配置
ayaoxinchao
linuxFTP服务器vsftp
检测是否安装了FTP
[root@localhost ~]# rpm -q vsftpd
如果未安装:package vsftpd is not installed 安装了则显示:vsftpd-2.0.5-28.el5累死的版本信息
安装FTP
运行yum install vsftpd命令,如[root@localhost ~]# yum install vsf
- 使用mongo-java-driver获取文档id和查找文档
BigBird2012
driver
注:本文所有代码都使用的mongo-java-driver实现。
在MongoDB中,一个集合(collection)在概念上就类似我们SQL数据库中的表(Table),这个集合包含了一系列文档(document)。一个DBObject对象表示我们想添加到集合(collection)中的一个文档(document),MongoDB会自动为我们创建的每个文档添加一个id,这个id在
- JSONObject以及json串
bijian1013
jsonJSONObject
一.JAR包简介
要使程序可以运行必须引入JSON-lib包,JSON-lib包同时依赖于以下的JAR包:
1.commons-lang-2.0.jar
2.commons-beanutils-1.7.0.jar
3.commons-collections-3.1.jar
&n
- [Zookeeper学习笔记之三]Zookeeper实例创建和会话建立的异步特性
bit1129
zookeeper
为了说明问题,看个简单的代码,
import org.apache.zookeeper.*;
import java.io.IOException;
import java.util.concurrent.CountDownLatch;
import java.util.concurrent.ThreadLocal
- 【Scala十二】Scala核心六:Trait
bit1129
scala
Traits are a fundamental unit of code reuse in Scala. A trait encapsulates method and field definitions, which can then be reused by mixing them into classes. Unlike class inheritance, in which each c
- weblogic version 10.3破解
ronin47
weblogic
版本:WebLogic Server 10.3
说明:%DOMAIN_HOME%:指WebLogic Server 域(Domain)目录
例如我的做测试的域的根目录 DOMAIN_HOME=D:/Weblogic/Middleware/user_projects/domains/base_domain
1.为了保证操作安全,备份%DOMAIN_HOME%/security/Defa
- 求第n个斐波那契数
BrokenDreams
今天看到群友发的一个问题:写一个小程序打印第n个斐波那契数。
自己试了下,搞了好久。。。基础要加强了。
&nbs
- 读《研磨设计模式》-代码笔记-访问者模式-Visitor
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
interface IVisitor {
//第二次分派,Visitor调用Element
void visitConcret
- MatConvNet的excise 3改为网络配置文件形式
cherishLC
matlab
MatConvNet为vlFeat作者写的matlab下的卷积神经网络工具包,可以使用GPU。
主页:
http://www.vlfeat.org/matconvnet/
教程:
http://www.robots.ox.ac.uk/~vgg/practicals/cnn/index.html
注意:需要下载新版的MatConvNet替换掉教程中工具包中的matconvnet:
http
- ZK Timeout再讨论
chenchao051
zookeepertimeouthbase
http://crazyjvm.iteye.com/blog/1693757 文中提到相关超时问题,但是又出现了一个问题,我把min和max都设置成了180000,但是仍然出现了以下的异常信息:
Client session timed out, have not heard from server in 154339ms for sessionid 0x13a3f7732340003
- CASE WHEN 用法介绍
daizj
sqlgroup bycase when
CASE WHEN 用法介绍
1. CASE WHEN 表达式有两种形式
--简单Case函数
CASE sex
WHEN '1' THEN '男'
WHEN '2' THEN '女'
ELSE '其他' END
--Case搜索函数
CASE
WHEN sex = '1' THEN
- PHP技巧汇总:提高PHP性能的53个技巧
dcj3sjt126com
PHP
PHP技巧汇总:提高PHP性能的53个技巧 用单引号代替双引号来包含字符串,这样做会更快一些。因为PHP会在双引号包围的字符串中搜寻变量, 单引号则不会,注意:只有echo能这么做,它是一种可以把多个字符串当作参数的函数译注: PHP手册中说echo是语言结构,不是真正的函数,故把函数加上了双引号)。 1、如果能将类的方法定义成static,就尽量定义成static,它的速度会提升将近4倍
- Yii框架中CGridView的使用方法以及详细示例
dcj3sjt126com
yii
CGridView显示一个数据项的列表中的一个表。
表中的每一行代表一个数据项的数据,和一个列通常代表一个属性的物品(一些列可能对应于复杂的表达式的属性或静态文本)。 CGridView既支持排序和分页的数据项。排序和分页可以在AJAX模式或正常的页面请求。使用CGridView的一个好处是,当用户浏览器禁用JavaScript,排序和分页自动退化普通页面请求和仍然正常运行。
实例代码如下:
- Maven项目打包成可执行Jar文件
dyy_gusi
assembly
Maven项目打包成可执行Jar文件
在使用Maven完成项目以后,如果是需要打包成可执行的Jar文件,我们通过eclipse的导出很麻烦,还得指定入口文件的位置,还得说明依赖的jar包,既然都使用Maven了,很重要的一个目的就是让这些繁琐的操作简单。我们可以通过插件完成这项工作,使用assembly插件。具体使用方式如下:
1、在项目中加入插件的依赖:
<plugin>
- php常见错误
geeksun
PHP
1. kevent() reported that connect() failed (61: Connection refused) while connecting to upstream, client: 127.0.0.1, server: localhost, request: "GET / HTTP/1.1", upstream: "fastc
- 修改linux的用户名
hongtoushizi
linuxchange password
Change Linux Username
更改Linux用户名,需要修改4个系统的文件:
/etc/passwd
/etc/shadow
/etc/group
/etc/gshadow
古老/传统的方法是使用vi去直接修改,但是这有安全隐患(具体可自己搜一下),所以后来改成使用这些命令去代替:
vipw
vipw -s
vigr
vigr -s
具体的操作顺
- 第五章 常用Lua开发库1-redis、mysql、http客户端
jinnianshilongnian
nginxlua
对于开发来说需要有好的生态开发库来辅助我们快速开发,而Lua中也有大多数我们需要的第三方开发库如Redis、Memcached、Mysql、Http客户端、JSON、模板引擎等。
一些常见的Lua库可以在github上搜索,https://github.com/search?utf8=%E2%9C%93&q=lua+resty。
Redis客户端
lua-resty-r
- zkClient 监控机制实现
liyonghui160com
zkClient 监控机制实现
直接使用zk的api实现业务功能比较繁琐。因为要处理session loss,session expire等异常,在发生这些异常后进行重连。又因为ZK的watcher是一次性的,如果要基于wather实现发布/订阅模式,还要自己包装一下,将一次性订阅包装成持久订阅。另外如果要使用抽象级别更高的功能,比如分布式锁,leader选举
- 在Mysql 众多表中查找一个表名或者字段名的 SQL 语句
pda158
mysql
在Mysql 众多表中查找一个表名或者字段名的 SQL 语句:
方法一:SELECT table_name, column_name from information_schema.columns WHERE column_name LIKE 'Name';
方法二:SELECT column_name from information_schema.colum
- 程序员对英语的依赖
Smile.zeng
英语程序猿
1、程序员最基本的技能,至少要能写得出代码,当我们还在为建立类的时候思考用什么单词发牢骚的时候,英语与别人的差距就直接表现出来咯。
2、程序员最起码能认识开发工具里的英语单词,不然怎么知道使用这些开发工具。
3、进阶一点,就是能读懂别人的代码,有利于我们学习人家的思路和技术。
4、写的程序至少能有一定的可读性,至少要人别人能懂吧...
以上一些问题,充分说明了英语对程序猿的重要性。骚年
- Oracle学习笔记(8) 使用PLSQL编写触发器
vipbooks
oraclesql编程活动Access
时间过得真快啊,转眼就到了Oracle学习笔记的最后个章节了,通过前面七章的学习大家应该对Oracle编程有了一定了了解了吧,这东东如果一段时间不用很快就会忘记了,所以我会把自己学习过的东西做好详细的笔记,用到的时候可以随时查找,马上上手!希望这些笔记能对大家有些帮助!
这是第八章的学习笔记,学习完第七章的子程序和包之后