北京网选赛第二题（最大仰望角度）
http://acm.hdu.edu.cn/showproblem.php?pid=5033
Building
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 931 Accepted Submission(s): 261
Special Judge
Problem Description
Once upon a time Matt went to a small town. The town was so small and narrow that he can regard the town as a pivot. There were some skyscrapers in the town, each located at position x
i with its height h
i. All skyscrapers located in different place. The skyscrapers had no width, to make it simple. As the skyscrapers were so high, Matt could hardly see the sky.Given the position Matt was at, he wanted to know how large the angle range was where he could see the sky. Assume that Matt's height is 0. It's guaranteed that for each query, there is at least one building on both Matt's left and right, and no building locate at his position.
Input
The first line of the input contains an integer T, denoting the number of testcases. Then T test cases follow.
Each test case begins with a number N(1<=N<=10^5), the number of buildings.
In the following N lines, each line contains two numbers, x i(1<=x i<=10^7) and h i(1<=h i<=10^7).
After that, there's a number Q(1<=Q<=10^5) for the number of queries.
In the following Q lines, each line contains one number q i, which is the position Matt was at.
Each test case begins with a number N(1<=N<=10^5), the number of buildings.
In the following N lines, each line contains two numbers, x i(1<=x i<=10^7) and h i(1<=h i<=10^7).
After that, there's a number Q(1<=Q<=10^5) for the number of queries.
In the following Q lines, each line contains one number q i, which is the position Matt was at.
Output
For each test case, first output one line "Case #x:", where x is the case number (starting from 1).
Then for each query, you should output the angle range Matt could see the sky in degrees. The relative error of the answer should be no more than 10^(-4).
Then for each query, you should output the angle range Matt could see the sky in degrees. The relative error of the answer should be no more than 10^(-4).
Sample Input
3 3 1 2 2 1 5 1 1 4 3 1 3 2 2 5 1 1 4 3 1 4 2 3 5 1 1 4
Sample Output
Case #1: 101.3099324740 Case #2: 90.0000000000 Case #3: 78.6900675260
分析：可以用单调栈来维护；
具体如下：
第一种单调递减情况是
栈中不需要维护中间两点，这个线段对于之后的观察员来说只有首尾两点的高度来决定；
第二种单调递减情况是
栈中需要维护这四个顶点因为从左向右走到足够远的地方，每个点的高度都有可能成为限制点；
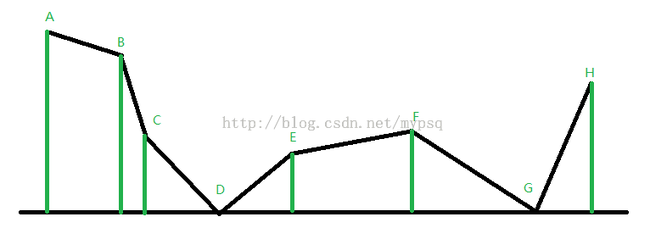
例如下图：
用q[]数组模拟栈，p[]数组记录按照x坐标排序的点A，B……；首先把A，A入栈，然后判断AAB是符合第几种单调情况；经判断把B入栈，然后判断ABC是符合第二种情况把C入栈，BCD符合第一种情况，把C出栈，发现此时ABD符合第二种，把D入栈，此时D的点是观察员的位置，所以他的左边应该是由B点的高度决定，然后判断BDE符合第一种，把D出栈，此时ABE符合第二种，把E入栈；然后BEF符合第一种把E出栈，ABF符合第二种把F入栈，接着BFG符合第二种把G入栈，G是观察员的位置，左边由F点的高度决定，一次类推。。。
对于右面的点，只需要按照上述原理从右向左判断一遍即可；
程序：
#include"stdio.h"
#include"string.h"
#include"stack"
#include"stdlib.h"
#include"iostream"
#include"algorithm"
#include"math.h"
#define M 200009
#define inf 100000000
#define eps 1e-10
#define PI acos(-1.0)
using namespace std;
struct node
{
double x,y;
int id;
}p[M],q[M],ans[M];
int cmp(node a,node b)
{
return a.x<b.x;
}
double cross(node a,node b,node c)
{
double px1=b.x-a.x;
double px2=c.x-a.x;
double py1=b.y-a.y;
double py2=c.y-a.y;
return px1*py2-px2*py1;
}
int main()
{
int T,n,i,m,kk=1;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(i=0;i<n;i++)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
p[i].id=i;
}
scanf("%d",&m);
for(i=n;i<m+n;i++)
{
scanf("%lf",&p[i].x);
p[i].y=0;
p[i].id=i;
}
sort(p,p+n+m,cmp);
q[0]=p[0];
q[1]=p[0];
int cnt=1;
for(i=1;i<m+n;i++)
{
while(cross(q[cnt-1],q[cnt],p[i])>-eps&&cnt-1>=0)
cnt--;
q[++cnt]=p[i];
if(p[i].y<eps)
{
ans[p[i].id].x=fabs(q[cnt-1].y/(q[cnt-1].x-q[cnt].x));
}
}
q[0]=q[1]=p[m+n-1];
cnt=1;
for(i=m+n-2;i>=0;i--)
{
while(cross(q[cnt-1],q[cnt],p[i])<eps&&cnt>=1)
cnt--;
q[++cnt]=p[i];
if(p[i].y<eps)
{
ans[p[i].id].y=fabs(q[cnt-1].y/(q[cnt-1].x-q[cnt].x));
}
}
printf("Case #%d:\n",kk++);
for(i=n;i<m+n;i++)
printf("%.10lf\n",(PI-atan(ans[i].x)-atan(ans[i].y))/PI*180);
}
}