算法分析 | 回溯法 | 01背包问题

零.前言

1.确立解空间

回溯法需要用到树的概念 . 这个树就是问题的解空间{x1,x2,x3....xn}.

其中,左右连线表示做出了某个选择;每个结点表示做出选择后的一个状态; 每一层代表一个数组元素

 

 

2.搜索解空间

①约束条件:满足某个条件才能向左子树扩展,表示放入物品.

cw:已装入重量;    w[i]:当前物品的重量;    W:总容积

cw + w[i] <= W                                                                                                          时间复杂度=O(1)

 

②限界条件:向右子树扩展,即使不放入该物品,最后也可能产生最优解

cp:当前价值;    rp:剩下物品的总价值;    bestp:计算过程中当前的最优解

cp+rp>=bestp              只有满足限界条件,才有向右子树扩展的价值                 rp需要累加得解,时间复杂度=O(n)

 

③编写程序

递归程序的编写,是要在逻辑上的二叉树中(实际并没有创建一棵树).按照广度遍历的顺序来写

树:   (+号写错了)                                                                             代码:

 

 

一.代码实现

#include"allh.h"
#include  //调用数组累加函数

vectorw{ 2,6,5,3 };		//物品的重量数组
vectorv{ 4,5,2,4 };		//价值数组

int W = 10;		//总装载空间
auto n = w.size();//记录物品数量

int cw = 0;			//记录当前重量
int cp = 0;			//记录当前价格
vector xx(n, 0);			//记录当前最优解

int bestp;			//记录最终最优值
vector bestx(n,1);		//记录最终最优解


//上界函数,计算(已装入物品价值+剩余总价值). 如果这个最大值仍小于bestp,则没有必要再往下递归
int  bound(int t)//t的实参是:当前物品的下一个
{
	int rp = 0;
	while (t < n)//从当前物品的下一个~n-1
	{
		rp += v[t];
		t++;
	}
	return cp + rp;
}

//递归求解最优解
void backtrack(int t)//第一个传入的实参是0
{
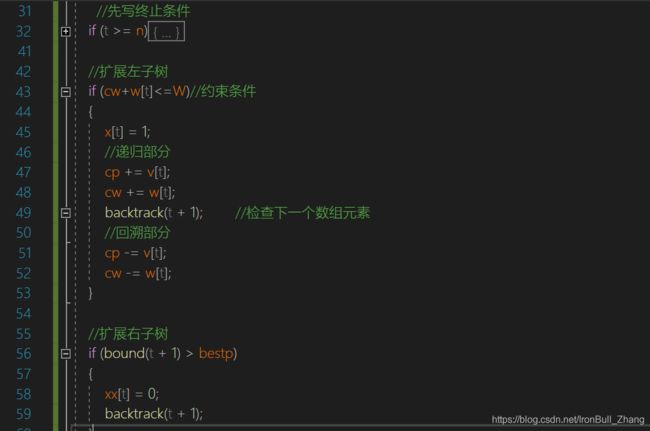
	  //先写终止条件
	if (t >= n)		//t=(0,n-1)表示还在计算,t=n表示已经计算完最后一个,开始清算
	{
		for (int i = 0; i < n; i++)
		{
			bestx[i] = xx[i];		//保存最优解
		}
		bestp = cp;				//保存最优值
		return;
	}

	//扩展左子树
	if (cw+w[t]<=W)//约束条件
	{
		xx[t] = 1; 
		//递归部分
		cp += v[t];
		cw += w[t];
		backtrack(t + 1);		//检查下一个数组元素
		//回溯部分
		cp -= v[t];
		cw -= w[t];
	}

	//扩展右子树
	if (bound(t + 1) > bestp)
	{
		xx[t] = 0;
		backtrack(t + 1);
	}

}

//调用递归函数backtrack()
void backpack()
{
	//初始化
	cw = 0;
	cp = 0;
	bestp = 0;
	int sumw=accumulate(w.begin(), w.end(), 0);			//记录总重量
	int sumv=accumulate(v.begin(), v.end(), 0);			//记录总价值

	//总重量<容积
	if (sumw < W)
	{
		bestp = sumv;
		cout << "全部商品都装得下\n";
		cout << "最大价值为:\t" << bestp;
		return;
	}

	backtrack(0);		//从[0]开始递归
	cout << "最大价值为:\t" << bestp<

二.Bug分析

本次没什么问题,有个变量名写错了.

 

三.算法优化

可以改进Bound()函数

原Bound()函数中,返回值为cp + rp  ,这个值太大了.  剩余物品重量rw可能 > 总容量W

先将物品数组按重量价值比排序,再求取上界

int bound_1(int t)
{
	int surplus = W - cw;//当前剩余容量
	int brp = 0;				//当前剩余价值
	while (t < n && w[t] < surplus)
	{
		surplus -= w[t];
		brp += v[t];
		t++;
	}
	if (t <= n)
	{
		brp += v[t] / w[t] * surplus;  //求上界时可以切割物品,求解时不允许
	}
	return cp + brp;
}

注意数据结构也要做修改.