HDU 3692 Shade of Hallelujah Mountain (计算几何,三维空间点的旋转,二维凸包)
Shade of Hallelujah Mountain
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 483 Accepted Submission(s): 93
Problem Description
On the planet Pandora, huge rocks are floating in the sky. Despite the beautiful scenery, these rocks bring some critical problem: they block the sunshine, and shade on the ground. Na'vi ("people" living on the planet) cannot grow plants in the shade because of the lack of sunshine. In order to predicate the amount of food they can get, they have to calculate the area of the shade.
Let’s assume the "sun" as a point-source of light, and the ground as a infinite flat plane. Also, to simplify this problem, assume all rocks are convex polyhedrons.
Now here is a mathematical problem. Given the position of the point-source of light, the position of a convex polyhedron and the position of an infinite plane, you are required to calculate the area of the shade. Please note that light travels in a strictly straight line and the light source and the convex polyhedron are on the same side of the plane. The light source is not placed in the convex polyhedron, nor on the polyhedron or on the plane.
Let’s assume the "sun" as a point-source of light, and the ground as a infinite flat plane. Also, to simplify this problem, assume all rocks are convex polyhedrons.
Now here is a mathematical problem. Given the position of the point-source of light, the position of a convex polyhedron and the position of an infinite plane, you are required to calculate the area of the shade. Please note that light travels in a strictly straight line and the light source and the convex polyhedron are on the same side of the plane. The light source is not placed in the convex polyhedron, nor on the polyhedron or on the plane.
Input
The input contains no more than 100 cases.
Each case contains several lines which are formatted as follows.
a b c d
n
x 1 y 1 z 1
x 2 y 2 z 2
......
x n y n z n
x 0 y 0 z 0
a, b, c and d means that the plane is ax+by+cz=d. n means the number of vertex of the convex polyhedron. It is guaranteed that n is no more than 100. Following it are n lines. Each line contains three float numbers, indicating the position of a point which is a vertex of the polyhedron. The last line also contains three float numbers, which means the position of the point-source of light.
The input is ended by a=0, b=0, c=0 and d=0.
Each case contains several lines which are formatted as follows.
a b c d
n
x 1 y 1 z 1
x 2 y 2 z 2
......
x n y n z n
x 0 y 0 z 0
a, b, c and d means that the plane is ax+by+cz=d. n means the number of vertex of the convex polyhedron. It is guaranteed that n is no more than 100. Following it are n lines. Each line contains three float numbers, indicating the position of a point which is a vertex of the polyhedron. The last line also contains three float numbers, which means the position of the point-source of light.
The input is ended by a=0, b=0, c=0 and d=0.
Output
For each case, if there is no shade on the plane, print “0.00”.
If the area of the shade is infinite, print “Infi”.
Otherwise, print out the area of the shade. Please round the result to two digits after the decimal point.
Here are some hints to help you implement rotation in 3-dimensional space.
Assume that there is a plane ax+by+cz=0 , and our task is to rotate the whole space so that the plane will be in the position z=0 .
As we all know, the normal vector of the plane is (a,b,c) , so after we rotate the space, the normal vector will be the z-axis. So we can only consider how to rotate the vector to the position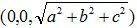 .
.
We can divide the process into 2 steps. First step, rotate the normal vector to . Second step, rotate
. Second step, rotate
 to
to
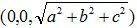 . Then apply the two rotation steps on the whole space, we can rotate the plane to a given position.
. Then apply the two rotation steps on the whole space, we can rotate the plane to a given position.
It is easy to implement the two steps. In first step, the third number in the normal vector does not change, so this is like rotation in a 2-dimensional space. Similarly, we implement the second step.
If the area of the shade is infinite, print “Infi”.
Otherwise, print out the area of the shade. Please round the result to two digits after the decimal point.
Hint
Here are some hints to help you implement rotation in 3-dimensional space.
Assume that there is a plane ax+by+cz=0 , and our task is to rotate the whole space so that the plane will be in the position z=0 .
As we all know, the normal vector of the plane is (a,b,c) , so after we rotate the space, the normal vector will be the z-axis. So we can only consider how to rotate the vector to the position
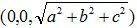 .
.
We can divide the process into 2 steps. First step, rotate the normal vector to
 . Second step, rotate
. Second step, rotate
 to
to
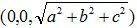 . Then apply the two rotation steps on the whole space, we can rotate the plane to a given position.
. Then apply the two rotation steps on the whole space, we can rotate the plane to a given position.
It is easy to implement the two steps. In first step, the third number in the normal vector does not change, so this is like rotation in a 2-dimensional space. Similarly, we implement the second step.
Sample Input
0 0 1 0 8 1 1 1 1 -1 1 -1 1 1 -1 -1 1 1 1 0 1 -1 0 -1 1 0 -1 -1 0 2 2 1 1 0 0 -2 8 1 1 1 1 1 -1 1 -1 1 1 -1 -1 -1 1 1 -1 1 -1 -1 -1 1 -1 -1 -1 2 0 0 1 1 1 1 0 0 0 0 0 0 0 0
Sample Output
Infi 64.00 0.00
Source
Recommend
axubiao
好题。
练习计算几何点的旋转和二维凸包。
//============================================================================ // Name : HDU3692.cpp // Author : kuangbin // Version : // Copyright : Your copyright notice // Description : //给出一个凸多面体,一个点光源和一个平面(多面体和光源在平面的同一侧), //求多面体在平面上的阴影面积(如果无穷大就输出Info,没有就为0)。 //就像Hint那里所提示的那样去做即可,把平面P:a*x+b*y+c*z=d旋转平移到 //平面z=0。方法有点巧妙,令vec=(a,b,c)X(0,0,1),则P绕vec做旋转逆时针 //旋转,旋转的角度为(a,b,c)和(0,0,1)之间的夹角,然后凸多面体上的点和 //预先选好的平面上的一点做相同的操作,然后根据预选的平面上的一点的z值 //就可以知道要平移多少了。最后就求凸多面体上的点在z=0平面上的投影点,再 //求这些点的凸包,计算凸包面积即可 //============================================================================ #include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <algorithm> #include <vector> using namespace std; const int MAXN=110; const double eps=1e-8; const double PI=acos(-1.0); inline int sign(double d) { if(d > eps)return 1; else if(d < -eps)return -1; else return 0; } struct Point //三维点坐标 { double x,y,z; Point(double xx=0,double yy=0,double zz=0):x(xx),y(yy),z(zz){} Point operator +(const Point p1) { return Point(x+p1.x,y+p1.y,z+p1.z); } Point operator -(const Point p1) { return Point(x-p1.x,y-p1.y,z-p1.z); } Point operator *(const Point p1) { return Point(y*p1.z-z*p1.y,z*p1.x-x*p1.z,x*p1.y-y*p1.x); } Point operator *(double d) { return Point(x*d,y*d,z*d); } Point operator /(double d) { return Point(x/d,y/d,z/d); } double operator ^(const Point p1) { return x*p1.x+y*p1.y+z*p1.z; } double getLen() { return sqrt(x*x+y*y+z*z); } void read() { scanf("%lf%lf%lf",&x,&y,&z); } }; Point ps[MAXN]; inline Point get_point(Point st,Point ed,Point tp)//求点tp在直线st-ed上的垂足 { double t1=(tp-st)^(ed-st); double t2=(ed-st)^(ed-st); double t=t1/t2; Point ans=st + (ed-st)*t; return ans; } inline double dist(Point st,Point ed) { return sqrt((ed-st)^(ed-st)); } Point rotate(Point st,Point ed,Point tp,double A)//沿着直线st-ed旋转角度A,从ed往st看是逆时针 { Point root=get_point(st,ed,tp); Point e=(ed-st)/dist(ed,st);//单位向量 Point r=tp-root; Point tmp=e*r; Point ans=r*cos(A)+tmp*sin(A)+root; return ans; } double a,b,c,d; int n; bool input() { scanf("%lf%lf%lf%lf",&a,&b,&c,&d); if(a==0&&b==0&&c==0&&d==0)return false; scanf("%d",&n); for(int i=0;i<=n;i++) ps[i].read(); return true; } //**************************************************** //二维凸包部分 struct point { double x,y; }; point list[MAXN]; int stack[MAXN],top; double cross(point p0,point p1,point p2)//p0p1 X p0p2 { return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); } double dis(point p1,point p2) { return sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y)); } bool cmp(point p1,point p2) { double tmp=cross(list[0],p1,p2); if(sign(tmp)>0)return true; else if(sign(tmp)==0&&dis(list[0],p1)<dis(list[0],p2))return true; else return false; } void init(int n) { point p0; int k; p0.x=list[0].x; p0.y=list[0].y; k=0; for(int i=1;i<n;i++) { if(p0.y>list[i].y || ((p0.y==list[i].y)&&(p0.x>list[i].x))) { p0.x=list[i].x; p0.y=list[i].y; k=i; } } list[k]=list[0]; list[0]=p0; sort(list+1,list+n,cmp); } void graham(int n) { int i; if(n==1) { top=0; stack[0]=0; return; } if(n==2) { top=1; stack[0]=0; stack[1]=1; return; } for(int i=0;i<n;i++)stack[i]=i; top=1; for(i=2;i<n;i++) { while(top>0 && cross(list[stack[top-1]],list[stack[top]],list[i])<=0)top--; top++; stack[top]=i; } } //**************************************************** void solve() { if(n<=2) { printf("0.00\n"); return; } Point p1(a,b,c);//法向量 Point tp(0,0,0); Point e(0,0,1); if(sign(a)!=0)tp.x=d/a; else if(sign(b)!=0)tp.y=d/b; else if(sign(c)!=0)tp.x=d/c; ps[n+1]=tp; Point vec=p1*e; double A=(e^p1)/p1.getLen(); A=acos(A); if(sign(A)!=0 && sign(A-PI)!=0) { Point p0(0,0,0); for(int i=0;i<=n+1;i++) ps[i]=rotate(p0,vec,ps[i],A); } for(int i=0;i<=n+1;i++) ps[i].z-=ps[n+1].z; if(sign(ps[n].z)<0) { for(int i=0;i<=n;i++) ps[i].z=-ps[i].z; } int cnt1=0;//记录ps[n]上方的点的个数 int cnt2=0;//记录和ps[n]高度一样的点的个数 for(int i=0;i<n;i++) { int k=sign(ps[i].z-ps[n].z); if(k>0)cnt1++; else if(k==0)cnt2++; } if(cnt1+cnt2==n) { printf("0.00\n"); return; } if(cnt1>0 || cnt2>0) { printf("Infi\n"); return; } for(int i=0;i<n;i++) { double u=ps[n].z/(ps[i].z-ps[n].z); list[i].x=ps[n].x+u*(ps[i].x-ps[n].x); list[i].y=ps[n].y+u*(ps[i].y-ps[n].y); } init(n); graham(n); double ans=0; for(int i=0;i<top;i++) ans+=(list[stack[i]].x * list[stack[i+1]].y - list[stack[i+1]].x*list[stack[i]].y); ans+=(list[stack[top]].x * list[stack[0]].y - list[stack[0]].x*list[stack[top]].y); printf("%.2lf\n",ans/2); } int main() { while(input())solve(); return 0; }