sort跟踪算法笔记
sort(simple online and realtime tracking)的组成
多目标跟踪有两种不同的实现方法:TBD(Tracking by detection)和DFT(Detection free tracking), 而sort方法则是TBD的代表,由目标检测+kalman filter + 匈牙利算法组成。另外,这里有个不错的人脸跟踪python实现,可以参考Face-Track-Detect-Extract
Kalman算法
sort中使用的kalman算法使用的是线性匀速模型,状态向量:
x ⃗ = [ u , v , s , r , u ˙ , v ˙ , s ˙ ] T \vec{x}=[u, v, s, r, \dot{u}, \dot{v}, \dot{s}]^T x=[u,v,s,r,u˙,v˙,s˙]T
这里的u,v是bbox的中心坐标, s为面积, r为横纵比,后面三个带点的为对应变量的速率,注意这里r是没有带点的,因为sort算法认为r是不变的常数。
kalman 算法的目的是融合测量值和估计值得到一个更好的测量值。
流程分为预测和更新两步。
- 预测
将状态向量x经过测量矩阵H的处理,变成一个修正了的测量值。
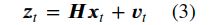
3中,z为测量值(也就是我们要预测的值,比如前面提到的人脸位置和宽高信息),x为状态向量, 定义如前面所示,不仅包含我们感兴趣的人脸位置宽高信息,还有额外的速度信息等。其中 H H H为观测矩阵,能够将包含冗余信息的x转换为我们要预测的值z,这个是一个固定的不需要更新的矩阵, v t v_t vt为测量噪声。在预测阶段我们只要关心上面的公式即可,可以看出,只要我们获取 x t x_t xt就可以算出z了,那么问题是 x t x_t xt是怎么来的呢?那么可以看更新阶段的内容。
可以看到,公式的左右两边分别是t和t-1,表示这一帧会关联上一帧的结果。
公式5可以看出,x是通过K求的,这里K称为kalman增益,通过K融合了新的测量值 z t z_t zt和估计值 x t ∣ t − 1 x_{t|t-1} xt∣t−1.那么这里的待定参数K是怎么来的呢,可以看下公式6.
公式6中,通过P,H和S算出K,其中P为状态向量的斜方差矩阵,表示两个向量的差异程度,
P t ∣ t − 1 = c o v ( x t − x t − 1 ) P_{t|t-1}=cov(x_t - x_{t-1}) Pt∣t−1=cov(xt−xt−1), 不过经过推导,可以转换为与x无关的公式2. H为固定矩阵, S为系统不确定性矩阵,定义参考公式4.
公式4中, S为 c o v ( z t − H x t ∣ t − 1 ) cov(z_t - H_{xt|t-1}) cov(zt−Hxt∣t−1),不过经过推导可以转换为与x无关的公式4. R为测量噪音矩阵。
1中, 这里的F是状态转移矩阵,这个也是固定的不会更新的, B为控制矩阵,比如可以给汽车一个油门信号来控制汽车跑得更快,一般都是0矩阵,u为噪音。
2中,P为状态向量的斜方差矩阵,表示两个向量的差异程度, P t ∣ t − 1 = c o v ( x t − x t − 1 ) P_{t|t-1}=cov(x_t - x_{t-1}) Pt∣t−1=cov(xt−xt−1)
不过经过推导,可以转换为与x无关的公式2.
kalman_filter中kalman算法的流程:
while True:
z = get_sensor_reading()
f.predict()
f.update(z)
do_something_with_estimate (f.x)
kalman算法中的符号意义:
P:协方差矩阵
z:测量值
R:测量噪音矩阵
Q:处理测量噪音矩阵
F:状态转移矩阵
H:测试函数
K:kalman增益
S:系统不确定性
匈牙利算法
一种关联算法,匈牙利算法能将两个集合中的元素按照一定规则进行两两匹配。
匹配时需要构建一个损失矩阵, 匹配成功后的集合损失最小。

