深度贝叶斯神经网络(Deep Bayesian Neural Networks)实现方法

深度贝叶斯神经网络(Deep Bayesian Neural Networks)实现方法

本文内容摘自： https://stefano-cosentino.medium.com/deep-bayesian-neural-networks-952763a9537

1. 目的是什么？

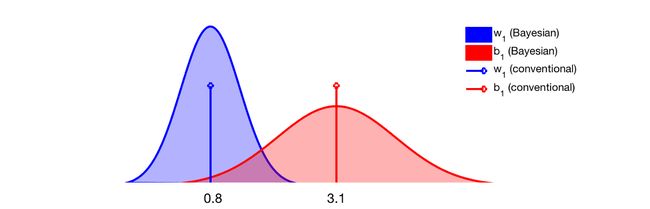
任何深度网络都有参数，通常以权重 $(w_1,w_2,...)$ 和偏差 $(b_1,b_2,...)$的形式存在。传统的方法（非贝叶斯）是通过最大似然估计（maximum likelihood estimation）仅学习这些参数的最优值。这些值都是标量(scalars)，如 $w_1=0.8$ 或 $b_1=3.1$。

而，贝叶斯方法对每个参数相关的分布(distributions)感兴趣。例如，在训练贝叶斯网络收敛后，上述的两个参数可能可以由以下两条高斯曲线（Gaussian curves）描述。

（训练传统网络和贝叶斯网络收敛后获得的两个参数（$w_1$ 和 $b_1$）的表示。）

拥有一个分布而不是单一的值有很多好处。首先，可以从分布中多次取样，查看对模型预测的影响。例如，经过多次取样，模型给出一致的预测，那么我们可以说网络对其做出的预测是自信的（confident）。

2. 难点是什么？

估计这些参数的分布是不容易的。这通常称为后验密度(posterior densities)，并使用贝叶斯公式进行估计。可以表示为：

$$p(w|x,y)=\frac{p(x,y|w)p(w)}{p(x,y)}=\frac{p(x,y|w)p(w)}{\int p(x,y|w)p(w)dw}$$

（贝叶斯公式。$x$ 和 $y$ 是输入和输出。分母中的积分需要对模型参数 $w$ 所有可能的值进行积分----这使计算变得非常困难。）

难点是分母----也称为模型证据（model evidence）。它需要对所有可能的参数值（即所有权重和偏差空间）进行积分，而这在实际中是做不到的。

做为替代，可以使用以下的伪数字方法，去近似积分的解。

• 用 MCMC 近似积分的方法
• 使用黑盒子变分推理（使用 edward 包）
• 使用 MC dropout

2.1 使用 MCMC 近似积分

由于计算贝叶斯公式的积分的解很难，可以通过使用 MCMC(马尔科夫链蒙特卡洛) 来近似积分的解。MCMC背后的原理真的很酷，建议大家阅读这个博客，通过代码和示例来理解 MCMC 背后的原理。撇开数学，这种方法是三个方法中最慢和最不吸引人的。

• 优点：理论上，MCMC最终可以获得最优的结果，其近似值接近于后验。
• 缺点：在实践中，它需要很长的时间来收敛，如果它曾经能收敛的话。

2.2 使用变分推理

变分推理（variational inference）是一种估计密度函数的方法，通过选择一个我们已知的分布（例如高斯），并逐步改变其参数，直到它看起来像我们想要计算的那个分布，即后验。改变参数不再需要计算复杂的微积分，这是一个优化过程，导数通常比积分更容易计算。我们要优化的由我们自己"捏造"的分布称为变分分布（variational distribution）。

• 优点：它比普通的MCMC方法快，而且通过使用edwar这样的函数包可以在几分钟内构建和运行贝叶斯网络。
• 缺点：对于非常深的贝叶斯网络来说，它可能会变得很慢，而且性能并不保证总是最佳的。

2.3 使用 MC dropout

Monte Carlo dropout (蒙特卡洛 dropout) 是2016年提出的一个理论¹，它通过使用一种称为 droput 的正则化方法提供了贝叶斯解释。

• 变分推理是一种贝叶斯方法，通过使用任意的分布，即前面介绍的变分分布来估计后验；
• 而，dropout 则是神经网络的一种正则化方法，在训练期间，部分神经元被随机打开或关闭，以防止网络依赖于特定的神经元。

MC dropout 的关键思想是：dropout 可以用来进行变分推理，其中变分分布来自于伯努利分布。MC 指的是 dropout 的采样以"Monte Carlo " 的方式进行。

伯努利分布 (Bernoulli distribution)，又名 $0-1$ 分布，是一种离散型概率分布。若伯努利试验成功，则伯努利随机变量取值为 $1$；若试验失败，则取值为 $0$。

在实践中，通过 MC dropout 可以将传统网络变成贝叶斯网络（在训练和验证期间，通过对每一层使用 dropout）；这相当于从伯努利分布中取样和度量模型的确信度(certainty)（多次取样预测的一致性）。也可以用 其他² 变分分布进行实验。

• 优点：将现有的深度网变成贝叶斯网是容易的。比其他技术要快，而且不需要推理框架。
• 缺点：对于计算要求高的（如实时）应用来说，在测试阶段的多次取样和预测可能过于昂贵。

完

---

1. https://arxiv.org/abs/1506.02142 ↩︎

2. https://arxiv.org/abs/1611.01639 ↩︎