Steger算法(Line_Gauss)-光条中心线提取(基于Hessian矩阵)
Steger算法(Line_Gauss)-光条中心线提取(基于Hessian矩阵)
- 算法背景介绍
- Hessian 矩阵与泰勒多项式
-
- 关于求t
- 导数与中心点、亚像素点
- 高斯函数作用
-
- 文献
算法背景介绍
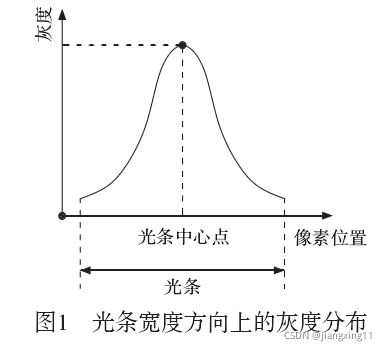
在线结构光视觉传感器中,由线激光器发射出的线结构光,在本质上为一个连续且具有一定厚度的空间光平面,而在目标表面上所形成的具有一定宽度的光条特征,即为该光平面与目标表面相交而成的交线。在该空间光平面的厚度方向上,光强近似服从高斯分布,因而在摄像机采集到的光条图像中,在沿着光条宽度的方向或光条的法线方向上,其灰度也会呈现出类似的高斯分布特点,即光条中心的灰度值大而光条边缘的灰度值小,如图1所示,因而光条中心线的提取任务就是要找到图像中的光条灰度的高斯分布中心。
如果熟悉Halcon软件的朋友应该对Line_Gauss算法非常了解,该算法的核心其实就是德国 Steger 博士最先提出的基于 Hessian 矩阵的亚像素级光条中心线的提取方法。
Steger算法的基本思路是首先通过 Hessian 矩阵获得光条的法线方向,然后在其法线方向上对像素灰度应用泰勒多项式展开而得到灰度分布函数,进而计算出光条中心的亚像素位置。由于光条特征的灰度在其法线方向上近似为高斯分布,因而越靠近光条中心点的像素,其灰度值越大。因此,对该法线方向上的灰度分布函数的二阶泰勒多项式求取极值,即可得到光条在该法线方向上的中心点坐标。
Hessian 矩阵与泰勒多项式
那么Hessian 矩阵是什么呢?在工程优化问题中,目标函数通常会以非线性多元函数的形式出现,这种函数形式非常复杂,不便于后续的进一步处理。因此,为了使问题简化,经常会将目标函数在某点的邻域内展开成泰勒多项式的形式,以此来近似或逼近原目标函数。在这个过程中,以矩阵形式表示的泰勒多项式就会涉及到 Hessian 矩阵,而且利用Hessian 矩阵可以判定多元函数的极值问题。
先来说一下多元函数的 Hessian 矩阵,对于一个实值多元函数 f(x1, x2, …, xn) 来说,如果函数 f 的多阶偏导数均存在,则定义函数 f 的 Hessian 矩阵H(f) 为:
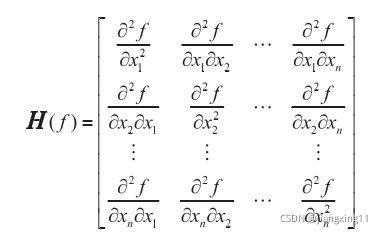
对于二维离散图像I(u, v) 来说,其 Hessian 矩阵可以表示为
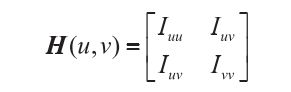
其中,u、v 分别表示像素的列坐标和行坐标;
I(u, v)即为像素 (u, v) 的灰度,因而可以将I(u, v) 视为该图像的灰度分布函数;Iuu、Iuv和Ivv分别表示二维高斯函数G(u, v)的二阶偏导数与图像I(u, v) 进行卷积运算的结果。
至于为什么要采用高斯函数进行卷积,可以看下一节。
那么回过头来看看泰勒展开,此处可以参考知乎关于多元函数的泰勒展开式的一些介绍和证明: https://zhuanlan.zhihu.com/p/33316479
一元函数在点 x k x_k xk处的泰勒展开式为:
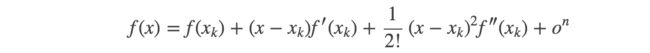
二元函数在点 ( x k , y k ) (x_k,y_k) (xk,yk)处的泰勒展开式为:
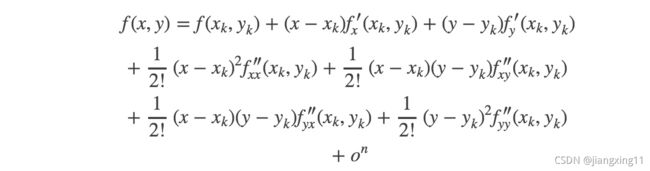
多元函数(n)在点 ( x k ) (x_k) (xk)处的泰勒展开式为:
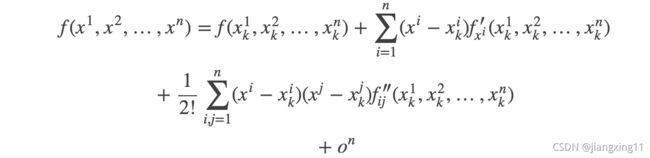
把泰勒展开式写成矩阵的形式,如下图所示,其中的 H ( x k ) H(x_k) H(xk)就是我们上面提到的Hessian矩阵,至此,泰勒展开与Hessian矩阵的联系就描述完成,注意其中的X,它是向量形式。
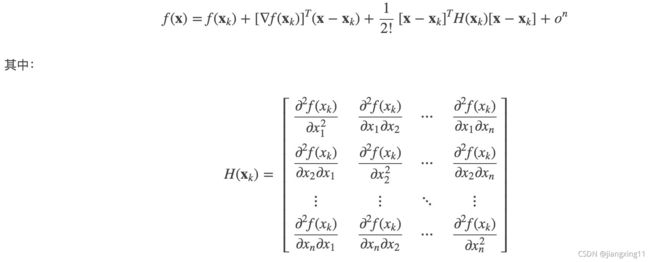
下面介绍二维图像中的泰勒展开与Hessian矩阵。对于图像中光条上的任意像素 ( u 0 , v 0 ) (u_0,v_0) (u0,v0),设其法线方向的单位方向向量为 e → = [ e u , e v ] \overrightarrow{e}=[e_u,e_v] e=[eu,ev],在该像素处将光条法线方向上的灰度分布函数 I ( u , v ) I(u,v) I(u,v) 沿方向 e → \overrightarrow{e} e 展开成泰勒多项式的形式,并忽略二阶以上的展开式。因此,光条法线方向上的像素 ( u 0 + t ⋅ e u , v 0 + t ⋅ e v ) (u_0+t·e_u, v_0+t·e_v) (u0+t⋅eu,v0+t⋅ev) 的灰度 I ( u 0 + t ⋅ e u , v 0 + t ⋅ e v ) I(u_0+t·e_u, v_0+t·e_v) I(u0+t⋅eu,v0+t⋅ev) 可以由像素 ( u 0 , v 0 ) (u_0,v_0) (u0,v0) 的灰度 I ( u 0 , v 0 ) I(u_0,v_0) I(u0,v0) 和二阶泰勒多项式表示为:
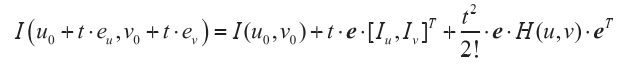 (5)
(5)
上式中的 I ( u 0 + t ⋅ e u , v 0 + t ⋅ e v ) I(u_0+t·e_u, v_0+t·e_v) I(u0+t⋅eu,v0+t⋅ev) 即为之前提到的 f ( x , y ) f(x,y) f(x,y),其中的 x = u 0 + t ⋅ e u , y = v 0 + t ⋅ e v x=u_0+t·e_u,y=v_0+t·e_v x=u0+t⋅eu,y=v0+t⋅ev,写成这样是为了方便理解
关于求t
之前参考了许多博主的文章,没能看懂关于 t t t 的求解过程,有的博主干脆直接跟论文一样跳过证明过程。本着寻根问底的态度,我还是把求解过程写一下。Steger博士写的论文截图如下:

式(5)即为光条在像素 ( u 0 , v 0 ) (u_0,v_0) (u0,v0) 处的横截面上的灰度分布函数,而使其一阶导数为零的点就是待提取的光条中心点。因此,令式(5)的一阶导数为零,即 ∂ I / ∂ t = 0 ∂I/∂t=0 ∂I/∂t=0 ,首先对式(5)关于 e → \overrightarrow{e} e求导可以得到:
∂ I ∂ t = e ⋅ [ I u , I v ] + t ⋅ e ⋅ H ( u , v ) ⋅ e T = 0 \frac{\partial I}{\partial t}=\mathbf{e}\cdot[I_u,I_v]+t\cdot\mathbf{e}\cdot\mathbf{H}(u,v)\cdot e^T=0 ∂t∂I=e⋅[Iu,Iv]+t⋅e⋅H(u,v)⋅eT=0
再将上式向量的形式改写成下式:
[ e u , e v ] ⋅ [ I u I v ] + t ⋅ [ e u , e v ] ⋅ [ I u u I u v I u v I v v ] ⋅ [ e u e v ] = 0 [e_u,e_v]\cdot \begin{bmatrix} I_u \\ I_v \end{bmatrix}+t\cdot[e_u,e_v] \cdot \begin{bmatrix} I_{uu} & I_{uv} \\ I_{uv} & I_{vv} \end{bmatrix} \cdot \begin{bmatrix} e_{u} \\ e_{v} \end{bmatrix}=0 [eu,ev]⋅[IuIv]+t⋅[eu,ev]⋅[IuuIuvIuvIvv]⋅[euev]=0
继续化简可得:
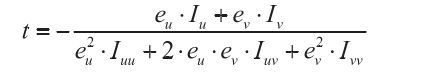
导数与中心点、亚像素点
如果 ( t ⋅ e u , t ⋅ e v ) ∈ [ − 0.5 , 0.5 ] × [ − 0.5 , 0.5 ] (t\cdot e_u,t\cdot e_v)∈[−0.5,0.5]×[−0.5,0.5] (t⋅eu,t⋅ev)∈[−0.5,0.5]×[−0.5,0.5],即一阶导数为零的点位于当前像素内,且 ( e u , e v ) (e_u,e_v) (eu,ev)方向的二阶导数大于指定的阈值,则该点 ( u 0 , v 0 ) (u_0,v_0) (u0,v0)为光条的中心点, ( e x , e y ) = ( u 0 + t ⋅ e u , v 0 + t ⋅ e v ) (e_x,e_y)=(u_0+t\cdot e_u,v_0+t\cdot e_v) (ex,ey)=(u0+t⋅eu,v0+t⋅ev)则为所求的亚像素坐标。
高斯函数作用
Steger博士在论文中提到,对于一维线检测,理想与现实中的线段存在偏差,以至于实际只能通过某种方式拟合成近似理想模型,这种方式其实就是利用高斯核进行卷积,论文中有个对比:
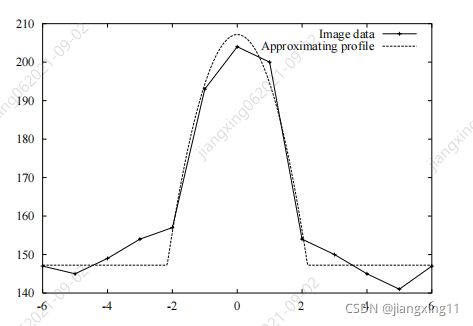
二维图像中,亮线在黑色背景中,激光线横截面理想模型(w=1,h=1)如下。

而实际情况下是不存在这样的激光线理想模型,一般都有一定宽度。那么如下图所示:

需要注意的是在求Hessian矩阵之前对图像进行高斯滤波时,根据文献[1]中,设置高斯方差 σ < ω 3 \sigma < \frac {\omega}{\sqrt{3}} σ<3ω ,其中 ω \omega ω为光条宽度。
文献
[1] Steger C. An unbiased detector of curvilinear structures. IEEE Trans Pattern Anal Mach Intell[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1998, 20(2):113-125.
[2] 毕超,周鹏,郝雪. 十字线结构光的光条中心线提取算法研究[J]. 航空精密制造技术, 2020, v.56;No.326(06):18-21.