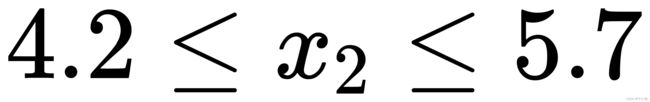计算智能课程设计(遗传算法求解无约束单目标优化问题)
写在前面
前天写完了基于传递闭包的模糊聚类,今天准备写“遗传算法求解无约束单目标优化问题”。昨天和npy玩了一下午,去齐白石艺术学院看了画展,一起在最高处看了夕阳,并在落日前接吻。
实验题目
遗传算法求解无约束单目标优化问题
实验目的
理解遗传算法原理,掌握遗传算法的基本求解步骤,包括选择、交叉、变异等,学会运用遗传算法求解无约束单目标优化问题。
背景知识
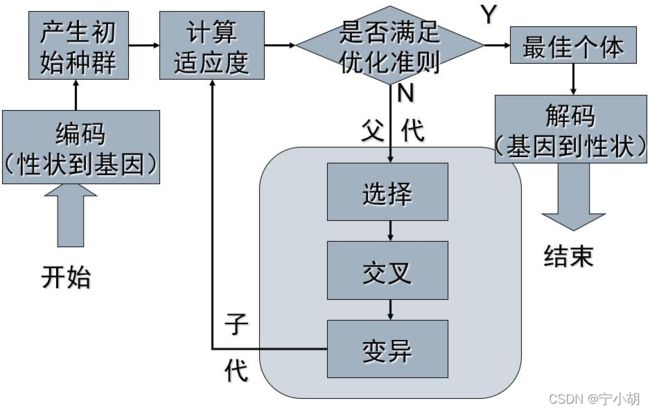
遗传算法(Genetic Algorithm)是借鉴生物界自然选择、适者生存遗传机制的一种随机搜索方法。遗传算法模拟了进化生物学中的遗传、突变、自然选择以及杂交等现象,是进化算法的一种。对于一个最优化问题,一定数量的候选解(每个候选解称为一个个体)的抽象表示(也称为染色体)的种群向更好的方向解进化,通过一代一代不断繁衍,使种群收敛于最适应的环境,从而求得问题的最优解。进化从完全随机选择的个体种群开始,一代一代繁殖、进化。在每一代中,整个种群的每个个体的适应度被评价,从当前种群中随机地选择多个个体(基于它们的适应度),通过自然选择、优胜劣汰和突变产生新的种群,该种群在算法的下一次迭代中成为当前种群。传统上,解一般用二进制表示(0 和 1 组成的串)。遗传算法的主要特点是直接对结构对象进行操作,不存在函数求导、连续、单峰的限定;具有内在的隐闭并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化搜索,自适应调整搜索方向,不需要确定的规则。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工智能等领域中的问题求解,已成为现代智能计算中的一项关键技术。
关键术语:
(1)个体( individuals):遗传算法中所处理的对象称为个体。个体通常可以含解的编码表示形式、适应度值等构成成分,因而可看成是一个结构整体。其中,主要成分是编码。
(2)种群(population):由个体构成的集合称为种群。
(3)位串(bit string):解的编码表示形式称为位串。解的编码表示可以是 0、1 二值串、0~9 十进制数字串或其他形式的串,可称为字符串或简称为串。位串和染色体(chromosome)相对应。在遗传算法的描述中,经常不加区分地使用位串和染色体这两个概念。位串/染色体与个体的关系:位串/染色体一般是个体的成分,个体还可含有适度值等成分。个体、染色体、位串或字符串有时在遗传算法中可不加区分地使用。
(4)种群规模(population scale):又称种群大小,指种群中所含个体的数目。
(5)基因(gene):位串中的每个位或元素统称为基因。基因反映个体的特征。同一位上的基因不同,个体的特征可能也不相同。基因对应于遗传学中的遗传物质单位。在 DNA 序列表示中,遗传物质单位也是用特定编码表示的。遗传算法中扩展了编码的概念,对于可行解,可用 0、1 二值、0~9 十个数字,以及其他形式的编码表示。例如,在 0、1 二值编码下,有一个串 S=1011,则其中的 1,0,1,1这 4 个元素分别称为基因。基因和位在遗传算法中也可不加区分地使用。
(6)适应度(fitness):个体对环境的适应程度称为适应度(fitness)。为了体现染色体的适应能力,通常引入一个对每个染色体都能进行度量的函数﹐称为适应度函数。
(7)选择(selection):在整个种群或种群的一部分中选择某个个体的操作。
(8)交叉(crossover):两个个体对应的一个或多个基因段的交换操作。
(9)变异(mutation):个体位串上某个基因的取值发生变化。如在 0、1 串表示下,某位的值从 0 变为 1,或由 1 变为 0。
遗传算法的基本流程如下:
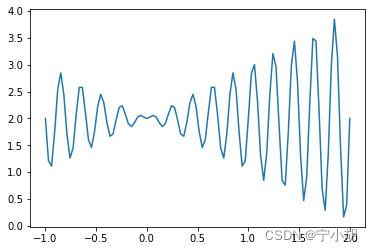
本案例意在说明如何使用遗传算法求解无约束单目标优化问题,即求一元函数:
在区间[-1, 2]上的最大值。该函数图像如下:
由图像可知该函数在在区间[-1, 2]上有很多极大值和极小值,对于求其最大值或最小值的问题,很多单点优化的方法(梯度下降等)就不适合,这种情况下可以考虑使用遗传算法。。
示例代码
import numpy as np
import matplotlib.pyplot as plt
def fun(x):
return x * np.sin(10*np.pi*x) + 2
Xs = np.linspace(-1, 2, 100)
np.random.seed(0) # 令随机数种子=0,确保每次取得相同的随机数
# 初始化原始种群
population = np.random.uniform(-1, 2, 10) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
for pop, fit in zip(population, fun(population)):
print("x=%5.2f, fit=%.2f" % (pop, fit))
plt.plot(Xs, fun(Xs))
plt.plot(population, fun(population), '*')
plt.show()
def encode(population, _min=-1, _max=2, scale=2**18, binary_len=18): # population必须为float类型,否则精度不能保证
# 标准化,使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
normalized_data = (population-_min) / (_max-_min) * scale
# 转成二进制编码
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
chroms = encode(population) # 染色体英文(chromosome)
for pop, chrom, fit in zip(population, chroms, fun(population)):
print("x=%.2f, chrom=%s, fit=%.2f" % (pop, chrom, fit))
def decode(popular_gene, _min=-1, _max=2, scale=2**18): # 先把x从2进制转换为10进制,表示这是第几份
# 乘以每份长度(长度/份数),加上起点,最终将一个2进制数,转换为x轴坐标
return np.array([(int(x, base=2)/scale*3)+_min for x in popular_gene])
fitness = fun(decode(chroms))
for pop, chrom, dechrom, fit in zip(population, chroms, decode(chroms), fitness):
print("x=%5.2f, chrom=%s, dechrom=%.2f, fit=%.2f" %
(pop, chrom, dechrom, fit))
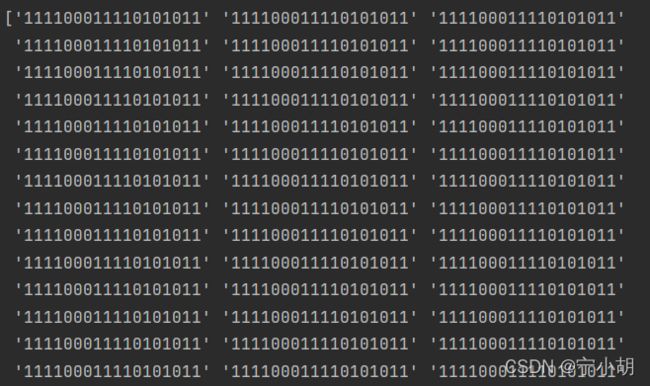
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
print(fitness)
def Select_Crossover(chroms, fitness, prob=0.6): # 选择和交叉
probs = fitness/np.sum(fitness) # 各个个体被选择的概率
probs_cum = np.cumsum(probs) # 概率累加分布
each_rand = np.random.uniform(size=len(fitness)) # 得到10个随机数,0到1之间
# 轮盘赌,根据随机概率选择出新的基因编码
# 对于each_rand中的每个随机数,找到被轮盘赌中的那个染色体
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
# 繁殖,随机配对(概率为0.6)
# 6这个数字怎么来的,根据遗传算法,假设有10个数,交叉概率为0.6,0和1一组,2和3一组。。。8和9一组,每组扔一个0到1之间的数字
# 这个数字小于0.6就交叉,则平均下来应有三组进行交叉,即6个染色体要进行交叉
pairs = np.random.permutation(
int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生6个随机数,乱排一下,分成二列
center = len(newX[0])//2 # 交叉方法采用最简单的,中心交叉法
for i, j in pairs:
# 在中间位置交叉
x, y = newX[i], newX[j]
newX[i] = x[:center] + y[center:] # newX的元素都是字符串,可以直接用+号拼接
newX[j] = y[:center] + x[center:]
return newX
chroms = Select_Crossover(chroms, fitness)
dechroms = decode(chroms)
fitness = fun(dechroms)
for gene, dec, fit in zip(chroms, dechroms, fitness):
print("chrom=%s, dec=%5.2f, fit=%.2f" % (gene, dec, fit))
# 对比一下选择和交叉之后的结果
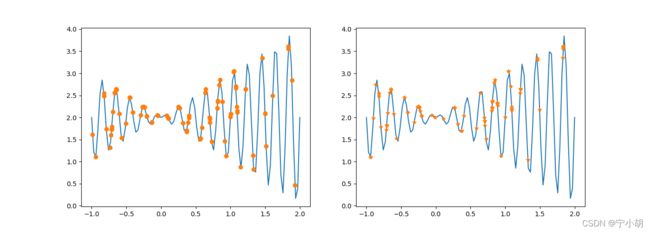
fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
axs1.plot(Xs, fun(Xs))
axs1.plot(population, fun(population), 'o')
axs2.plot(Xs, fun(Xs))
axs2.plot(dechroms, fitness, '*')
plt.show()
# 输入一个原始种群1,输出一个变异种群2 函数参数中的冒号是参数的类型建议符,告诉程序员希望传入的实参的类型。函数后面跟着的箭头是函数返回值的类型建议符,用来说明该函数返回的值是什么类型。
def Mutate(chroms: np.array):
prob = 0.1 # 变异的概率
clen = len(chroms[0]) # chroms[0]="111101101 000010110" 字符串的长度=18
m = {'0': '1', '1': '0'} # m是一个字典,包含两对:第一对0是key而1是value;第二对1是key而0是value
newchroms = [] # 存放变异后的新种群
each_prob = np.random.uniform(size=len(chroms)) # 随机10个数
for i, chrom in enumerate(chroms): # enumerate的作用是整一个i出来
if each_prob[i] < prob: # 如果要进行变异(i的用处在这里)
pos = np.random.randint(clen) # 从18个位置随机中找一个位置,假设是7
# 0~6保持不变,8~17保持不变,仅将7号翻转,即0改为1,1改为0。注意chrom中字符不是1就是0
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom) # 无论if是否成立,都在newchroms中增加chroms的这个元素
return np.array(newchroms) # 返回变异后的种群
newchroms = Mutate(chroms)
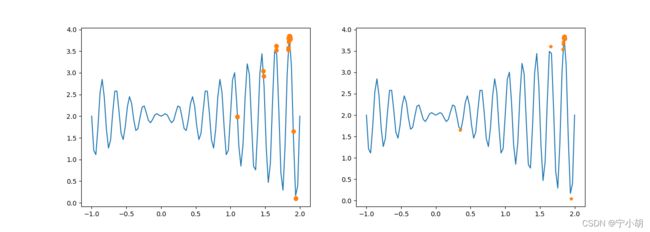
def DrawTwoChroms(chroms1, chroms2, fitfun): # 画2幅图,左边是旧种群,右边是新种群,观察平行的两幅图可以看出有没有差异
Xs = np.linspace(-1, 2, 100)
fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
dechroms = decode(chroms1)
fitness = fitfun(dechroms)
axs1.plot(Xs, fitfun(Xs))
axs1.plot(dechroms, fitness, 'o')
dechroms = decode(chroms2)
fitness = fitfun(dechroms)
axs2.plot(Xs, fitfun(Xs))
axs2.plot(dechroms, fitness, '*')
plt.show()
# 对比一下变异前后的结果
DrawTwoChroms(chroms, newchroms, fun)
# 上述代码只是执行了一轮,这里反复迭代
np.random.seed(0) #
population = np.random.uniform(-1, 2, 100) # 这次多找一些点
chroms = encode(population)
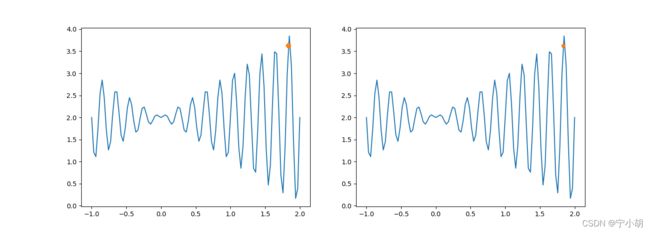
for i in range(1000):
fitness = fun(decode(chroms))
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
newchroms = Mutate(Select_Crossover(chroms, fitness))
if i % 300 == 1:
DrawTwoChroms(chroms, newchroms, fun)
chroms = newchroms
DrawTwoChroms(chroms, newchroms, fun)
实验内容
运行和理解示例代码,回答下列问题:
1)代码第 64 行的语义是什么?两个[0]各自代表什么?最后 newX 有几个元素?
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
2)代码第 70 行的语义是什么?为什么要除以 2 再乘以 2?reshape 中的-1 表示什么?
pairs = np.random.permutation(
int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生 6 个随机数乱排一下分成二列
3)请结合 Mutate 函数的内容,详述变异是如何实现的。
4)将代码第 145 行修改为 newchroms = Select_Crossover(chroms, fitness),即不再执行变异,执行结果有什么不同,为什么会出现这种变化?
5)轮盘让个体按概率被选择,对于适应度最高的个体而言,虽然被选择的概率高,但仍有可能被淘汰,从而在进化过程中失去当前最优秀的个体。一种改进方案是,让适应度最高的那个个体不参与选择,而是直接进入下一轮(直接晋级),这种方案被称为精英选择(elitist selection)。请修改Select 部分的代码,实现这一思路。
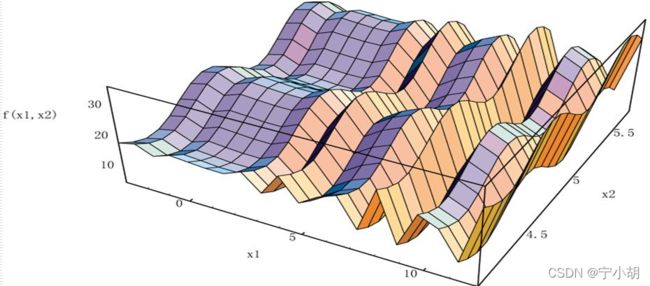
6)【选做】请借鉴示例代码,实现教材 P57 的例 2.6.1,即用遗传算法求解下列二元函数的最大值。
实验结果与分析
第一题
1)代码第 64 行的语义是什么?两个[0]各自代表什么?最后 newX 有几个元素?
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
经过拆分,得到结果:

上面的代码等于

其中[]中的for为列表生成式,返回一个列表。第一个[0]表示np.where()生成tuple元组中数组的行索引,np.where()[0]的值是tuple中的第一个数组,由于本例只有一个数组,故只返回一个一维数组,第二个[0]是该一维数组的首位元素。
最后newX一共有100个元素。
第二题
2)代码第 70 行的语义是什么?为什么要除以 2 再乘以 2?reshape 中的-1 表示什么?
pairs = np.random.permutation(
int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生 6 个随机数乱排一下分成二列
-
随机生成6个在[0,5]之间的数字,并将其排列成二维的形状是(3,2)的数组。
-
prob可能是奇数,这样乘上去没法取到整数分组,所以要//2取整。染色体是两两配对,所以要乘2。
-
reshape中的-1表示,通过列数对数组的行数进行自动计算。新的shape属性应该要与原来的配套,如果等于-1的话,那么Numpy会根据剩下的维度计算出数组的另外一个shape属性值。
第三题
3)请结合 Mutate 函数的内容,详述变异是如何实现的。
def Mutate(chroms: np.array):
prob = 0.1 # 变异的概率
clen = len(chroms[0]) # chroms[0]="111101101 000010110" 字符串的长度=18
m = {'0': '1', '1': '0'} # m是一个字典,包含两对:第一对0是key而1是value;第二对1是key而0是value
newchroms = [] # 存放变异后的新种群
each_prob = np.random.uniform(size=len(chroms)) # 随机10个数
for i, chrom in enumerate(chroms): # enumerate的作用是整一个i出来
if each_prob[i] < prob: # 如果要进行变异(i的用处在这里)
pos = np.random.randint(clen) # 从18个位置随机中找一个位置,假设是7
# 0~6保持不变,8~17保持不变,仅将7号翻转,即0改为1,1改为0。注意chrom中字符不是1就是0
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom) # 无论if是否成立,都在newchroms中增加chroms的这个元素
return np.array(newchroms) # 返回变异后的种群
- 首先,得到变异概率与单个染色体的长度(二进制数位数),再利用字典对变异的两种情况做一个存储。
- newchroms是存放变异后新种群的array。
- 通过each_prob计算出每个染色体的随机变异概率
- 遍历染色体,如果随机变异概率低于变异概率,则发生变异
- 发生变异,通过计算pos,从染色体中随机找个位置变异,即二进制数某个位发生突变
- 无论染色体是否发生变异,都在新种群中添加染色体(发生突变的与岁月静好的都算)
- 返回整个新的种群
染色体进行过交叉后,不再发生变异。少了一次变异,新种群与原种群概率上讲,差异要更小一些。
第五题
5)轮盘让个体按概率被选择,对于适应度最高的个体而言,虽然被选择的概率高,但仍有可能被淘汰,从而在进化过程中失去当前最优秀的个体。一种改进方案是,让适应度最高的那个个体不参与选择,而是直接进入下一轮(直接晋级),这种方案被称为精英选择(elitist selection)。请修改Select 部分的代码,实现这一思路。
def Select_Crossover(chroms, fitness, prob=0.6): # 选择和交叉
probs = fitness/np.sum(fitness) # 各个个体被选择的概率
# 修改代码处
max_probs = probs[np.argmax(probs)]
ak = chroms[np.argmax(probs)]
np.delete(chroms,np.argmax(probs))
np.delete(probs,np.argmax(probs))
# 修改代码处
probs_cum = np.cumsum(probs) # 概率累加分布
each_rand = np.random.uniform(size=len(fitness)) # 得到10个随机数,0到1之间
# 轮盘赌,根据随机概率选择出新的基因编码
# 对于each_rand中的每个随机数,找到被轮盘赌中的那个染色体
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
# 繁殖,随机配对(概率为0.6)
# 6这个数字怎么来的,根据遗传算法,假设有10个数,交叉概率为0.6,0和1一组,2和3一组。。。8和9一组,每组扔一个0到1之间的数字
# 这个数字小于0.6就交叉,则平均下来应有三组进行交叉,即6个染色体要进行交叉
pairs = np.random.permutation(
int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生6个随机数,乱排一下,分成二列
center = len(newX[0])//2 # 交叉方法采用最简单的,中心交叉法
for i, j in pairs:
# 在中间位置交叉
x, y = newX[i], newX[j]
newX[i] = x[:center] + y[center:] # newX的元素都是字符串,可以直接用+号拼接
newX[j] = y[:center] + x[center:]
# 修改代码处
np.append(newX,ak)
np.append(probs,max_probs )
# 修改代码处
return newX
第六题
代码思路
基于源代码与教材,对代码进行了如下修改:
因为要求二元函数的最大值,所以需要两个变量,x与y。这样一来,所需的种群就要有两批,设为chroms_x与chroms_y去对应,接下来需要对chroms1与chroms2进行编码和解码。代码如下。
# 初始化原始种群
population_x = np.random.uniform(-2.9, 12.0, 10) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
population_y = np.random.uniform(4.2, 5.7, 10)
def encode_x(population, _min=-2.9, _max=12.0, scale=2**21, binary_len=21): # population必须为float类型,否则精度不能保证
# 标准化,使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
normalized_data = (population-_min) / (_max-_min) * scale
# 转成二进制编码
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
def encode_y(population, _min=4.2, _max=5.7, scale=2**18, binary_len=18): # population必须为float类型,否则精度不能保证
# 标准化,使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
normalized_data = (population-_min) / (_max-_min) * scale
# 转成二进制编码
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
def decode_x(popular_gene, _min=-2.9, _max=12.0, scale=2**21): # 先把x从2进制转换为10进制,表示这是第几份
# 乘以每份长度(长度/份数),加上起点,最终将一个2进制数,转换为x轴坐标
return np.array([(int(x, base=2)/scale*14.9)+_min for x in popular_gene])
def decode_y(popular_gene, _min=4.2, _max=5.7, scale=2**18): # 先把x从2进制转换为10进制,表示这是第几份
# 乘以每份长度(长度/份数),加上起点,最终将一个2进制数,转换为x轴坐标
return np.array([(int(x, base=2)/scale*1.5)+_min for x in popular_gene])
chroms_x的染色体长度为21,chroms_y的长度为18,在编写编码和解码的代码中,分别要写两个函数,有所不同。按题目要求,需要将两段种群基因拼接起来,所以还需要设置第三个拼接后的种群chroms_v,以及对应的编码函数。变异后,需要将两个种群重新拆离,生成chroms_x和chroms_y去求函数。这里就需要一个解码过程。代码如下:
def encode_v(population_x,population_y):
chroms_x = encode_x(population_x)
chroms_y = encode_y(population_y)
chroms_v = np.char.add(chroms_x,chroms_y)
return chroms_v
def decode_v(chroms_v):
chroms_x = []
chroms_y = []
for chv in chroms_v:
tempx = chv[:21]
tempy = chv[21:]
chroms_x.append(tempx)
chroms_y.append(tempy)
dechroms_x = decode_x(chroms_x)
dechromx_y = decode_y(chroms_y)
return dechroms_x,dechromx_y
变异过程与源代码无异,只是将中心交叉改为了随机交叉。
def Select_Crossover(chroms, fitness, prob=0.6): # 选择和交叉
probs = fitness/np.sum(fitness) # 各个个体被选择的概率
probs_cum = np.cumsum(probs) # 概率累加分布
each_rand = np.random.uniform(size=len(fitness)) # 得到10个随机数,0到1之间
# 轮盘赌,根据随机概率选择出新的基因编码
# 对于each_rand中的每个随机数,找到被轮盘赌中的那个染色体
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
# 繁殖,随机配对(概率为0.6)
# 6这个数字怎么来的,根据遗传算法,假设有10个数,交叉概率为0.6,0和1一组,2和3一组。。。8和9一组,每组扔一个0到1之间的数字
# 这个数字小于0.6就交叉,则平均下来应有三组进行交叉,即6个染色体要进行交叉
pairs = np.random.permutation(int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生6个随机数,乱排一下,分成二列
point = np.random.randint(38) # 交叉方法采用随即交叉法
for i, j in pairs:
# 在中间位置交叉
x, y = newX[i], newX[j]
newX[i] = x[:point] + y[point:] # newX的元素都是字符串,可以直接用+号拼接
newX[j] = y[:point] + x[point:]
return newX
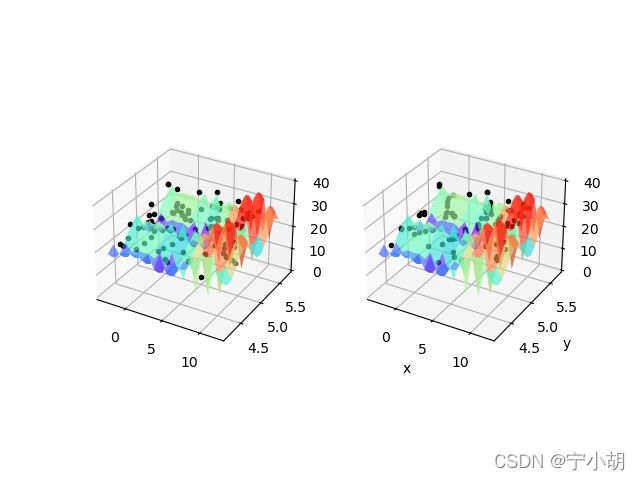
求出函数,要将数据可视化,我们作三维图进行对比表示。
# 画出迭代过程中的寻求二元函数极大值的变化图象
def DrawMax(x_data,y_data):
plt.figure()
ax = plt.gca()
ax.set_xlim(0,1000)
ax.set_ylim(0,40)
ax.locator_params('x',nbins=10)
ax.locator_params('y',nbins=8)
plt.plot(x_data,y_data)
plt.show()
# 画出对比函数图像
def DrawTwoChroms(chroms1, chroms2, fitfun): # 画2幅图,左边是旧种群,右边是新种群,观察平行的两幅图可以看出有没有差异
# 新建一个画布
figure = plt.figure()
# 新建一个3d绘图对象
ax1 = figure.add_subplot(1,2,1,projection='3d')
ax2 = figure.add_subplot(1,2,2,projection='3d')
# 生成x, y 的坐标集 (-2,2) 区间,间隔为 0.1
x = np.linspace(-2.9, 12.0, 20)
y = np.linspace(4.2, 5.7, 18)
# 生成网格矩阵
X, Y = np.meshgrid(x,y)
# 定义x,y 轴名称
plt.xlabel("x")
plt.ylabel("y")
# 设置间隔和颜色
#ax.plot_wireframe(X,Y,Z)
ax1.set_zlim(0, 40)
ax2.set_zlim(0, 40)
dechroms_x,dechroms_y = decode_v(chroms1)
fitness = fitfun(dechroms_x,dechroms_y)
ax1.plot_surface(X, Y, fitfun(X,Y), rstride=3, cstride=2, cmap="rainbow",alpha=0.65)
ax1.plot(dechroms_x,dechroms_y,fitness,'k.')
newdechroms_x,newdechroms_y = decode_v(chroms2)
fitness = fitfun(newdechroms_x,newdechroms_y)
ax2.plot_surface(X, Y, fitfun(X,Y), rstride=3, cstride=2, cmap="rainbow",alpha=0.65)
ax2.plot(newdechroms_x,newdechroms_y,fitness,'k.')
plt.show()
最后看一下主函数
np.random.seed(0)
population_x = np.random.uniform(-2.9, 12.0, 100) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
population_y = np.random.uniform(4.2, 5.7, 100)
chroms_v = encode_v(population_x,population_y)
x_data=[]
for i in range(1001):
x_data.append(i)
y_data = []
for i in range(1000):
dechroms_x,dechroms_y = decode_v(chroms_v)
fitness = fun(dechroms_x,dechroms_y)
fitmax = np.max(fitness)
y_data.append(fitmax)
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
newchroms_v = Mutate(Select_Crossover(chroms_v, fitness))
if i % 300 == 1:
DrawTwoChroms(chroms_v, newchroms_v, fun)
chroms_v = newchroms_v
dechroms_x,dechroms_y = decode_v(chroms_v)
fitness = fun(dechroms_x,dechroms_y)
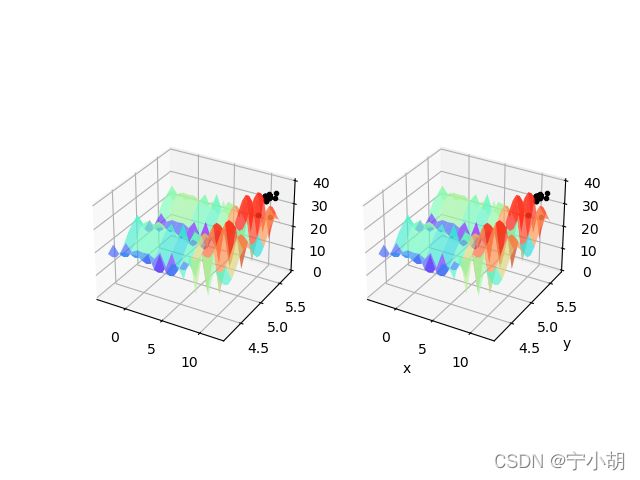
fitmax = np.max(fitness)
y_data.append(fitmax)
DrawTwoChroms(chroms_v, newchroms_v, fun)
print(len(y_data))
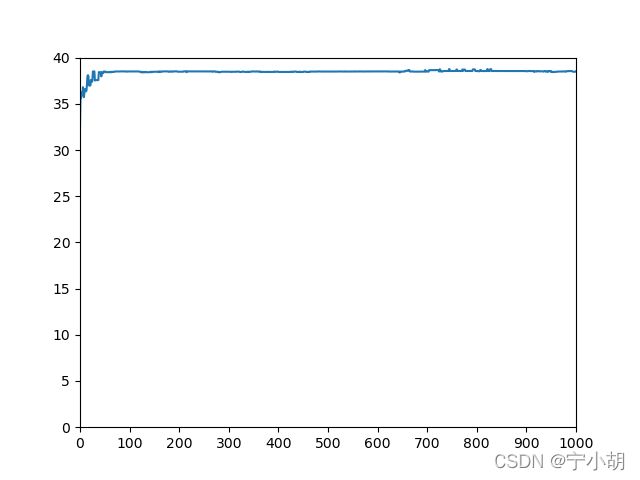
DrawMax(x_data,y_data)
print('函数的最大值为:')
print(np.max(fitness))
完整代码:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def fun(x,y):
return 21.5+x*np.sin(4*x*np.pi)+y*np.sin(20*y*np.pi)
Xs = np.linspace(-2.9, 12.0, 100)
Ys = np.linspace(4.2, 5.7, 100)
np.random.seed(0) # 令随机数种子=0,确保每次取得相同的随机数
# 初始化原始种群
population_x = np.random.uniform(-2.9, 12.0, 10) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
population_y = np.random.uniform(4.2, 5.7, 10)
for popx, popy, fit in zip(population_x,population_y,fun(population_x,population_y)):
print("x=%5.2f, y=%5.2f, fit=%.2f" % (popx,popy,fit))
# 新建一个画布
figure = plt.figure()
# 新建一个3d绘图对象
ax = Axes3D(figure)
# 生成x, y 的坐标集 (-2,2) 区间,间隔为 0.1
x = np.linspace(-2.9, 12.0, 20)
y = np.linspace(4.2, 5.7, 17)
# 生成网格矩阵
X, Y = np.meshgrid(x,y)
# 定义x,y 轴名称
plt.xlabel("x")
plt.ylabel("y")
Z= 21.5+X*np.sin(4*X*np.pi)+Y*np.sin(20*Y*np.pi)
# 设置间隔和颜色
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap="rainbow",alpha=0.5)
#ax.plot_wireframe(X,Y,Z)
ax.set_zlim(0, 40)
ax.plot(population_x,population_y,fun(population_x,population_y),'ko')
# 展示
plt.show()
def encode_x(population, _min=-2.9, _max=12.0, scale=2**21, binary_len=21): # population必须为float类型,否则精度不能保证
# 标准化,使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
normalized_data = (population-_min) / (_max-_min) * scale
# 转成二进制编码
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
def encode_y(population, _min=4.2, _max=5.7, scale=2**18, binary_len=18): # population必须为float类型,否则精度不能保证
# 标准化,使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
normalized_data = (population-_min) / (_max-_min) * scale
# 转成二进制编码
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
def encode_v(population_x,population_y):
chroms_x = encode_x(population_x)
chroms_y = encode_y(population_y)
chroms_v = np.char.add(chroms_x,chroms_y)
return chroms_v
# 染色体英文(chromosome)
# chroms_x = encode_x(population_x)
# chroms_y = encode_y(population_y)
chroms_v = encode_v(population_x,population_y)
print(chroms_v)
# for popx, popy, chromx_x, chromx_y, fit in zip(population_x, population_y, chroms_x, chroms_y, fun(population_x,population_y)):
# print("x=%.2f, x=%.2f, chrom_x=%s, chrom_y=%s, fit=%.2f" % (popx, popy, chromx_x, chromx_y, fit))
def decode_x(popular_gene, _min=-2.9, _max=12.0, scale=2**21): # 先把x从2进制转换为10进制,表示这是第几份
# 乘以每份长度(长度/份数),加上起点,最终将一个2进制数,转换为x轴坐标
return np.array([(int(x, base=2)/scale*14.9)+_min for x in popular_gene])
def decode_y(popular_gene, _min=4.2, _max=5.7, scale=2**18): # 先把x从2进制转换为10进制,表示这是第几份
# 乘以每份长度(长度/份数),加上起点,最终将一个2进制数,转换为x轴坐标
return np.array([(int(x, base=2)/scale*1.5)+_min for x in popular_gene])
def decode_v(chroms_v):
chroms_x = []
chroms_y = []
for chv in chroms_v:
tempx = chv[:21]
tempy = chv[21:]
chroms_x.append(tempx)
chroms_y.append(tempy)
dechroms_x = decode_x(chroms_x)
dechromx_y = decode_y(chroms_y)
return dechroms_x,dechromx_y
dechroms_x,dechroms_y = decode_v(chroms_v)
print(dechroms_x)
print(dechroms_y)
fitness = fun(dechroms_x,dechroms_y)
print(fitness)
# for popx, popy, chromx_x, chromx_y, dechromx_x, dechromx_y, fit in zip(population_x, population_y, chroms_x, chroms_y, fun(population_x,population_y)):
# print("x=%.2f, x=%.2f, chrom_x=%s, chrom_y=%s, dechrom_x=%.2f, dechrom_y=%.2f, fit=%.2f" % (popx, popy, chromx_x, chromx_y, dechromx_x, dechromx_y, fit))
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
print(fitness)
def Select_Crossover(chroms, fitness, prob=0.6): # 选择和交叉
probs = fitness/np.sum(fitness) # 各个个体被选择的概率
probs_cum = np.cumsum(probs) # 概率累加分布
each_rand = np.random.uniform(size=len(fitness)) # 得到10个随机数,0到1之间
# 轮盘赌,根据随机概率选择出新的基因编码
# 对于each_rand中的每个随机数,找到被轮盘赌中的那个染色体
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
for rand in each_rand])
# 繁殖,随机配对(概率为0.6)
# 6这个数字怎么来的,根据遗传算法,假设有10个数,交叉概率为0.6,0和1一组,2和3一组。。。8和9一组,每组扔一个0到1之间的数字
# 这个数字小于0.6就交叉,则平均下来应有三组进行交叉,即6个染色体要进行交叉
pairs = np.random.permutation(int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生6个随机数,乱排一下,分成二列
point = np.random.randint(38) # 交叉方法采用随即交叉法
for i, j in pairs:
# 在中间位置交叉
x, y = newX[i], newX[j]
newX[i] = x[:point] + y[point:] # newX的元素都是字符串,可以直接用+号拼接
newX[j] = y[:point] + x[point:]
return newX
chroms_v = Select_Crossover(chroms_v, fitness)
dechroms_x,dechroms_y = decode_v(chroms_v)
fitness = fun(dechroms_x,dechroms_y)
# for gene, dec, fit in zip(chroms, dechroms, fitness):
# print("chrom=%s, dec=%5.2f, fit=%.2f" % (gene, dec, fit))
# 对比一下选择和交叉之后的结果
# fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
# axs1.plot(Xs, fun(Xs))
# axs1.plot(population, fun(population), 'o')
# axs2.plot(Xs, fun(Xs))
# axs2.plot(dechroms, fitness, '*')
# plt.show()
# 输入一个原始种群1,输出一个变异种群2 函数参数中的冒号是参数的类型建议符,告诉程序员希望传入的实参的类型。函数后面跟着的箭头是函数返回值的类型建议符,用来说明该函数返回的值是什么类型。
def Mutate(chroms: np.array):
prob = 0.1 # 变异的概率
clen = len(chroms[0]) # chroms[0]="111101101 000010110" 字符串的长度=18
m = {'0': '1', '1': '0'} # m是一个字典,包含两对:第一对0是key而1是value;第二对1是key而0是value
newchroms = [] # 存放变异后的新种群
each_prob = np.random.uniform(size=len(chroms)) # 随机10个数
for i, chrom in enumerate(chroms): # enumerate的作用是整一个i出来
if each_prob[i] < prob: # 如果要进行变异(i的用处在这里)
pos = np.random.randint(clen) # 从18个位置随机中找一个位置,假设是7
# 0~6保持不变,8~17保持不变,仅将7号翻转,即0改为1,1改为0。注意chrom中字符不是1就是0
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom) # 无论if是否成立,都在newchroms中增加chroms的这个元素
return np.array(newchroms) # 返回变异后的种群
newchroms_v = Mutate(chroms_v)
def DrawMax(x_data,y_data):
plt.figure()
ax = plt.gca()
ax.set_xlim(0,1000)
ax.set_ylim(0,40)
ax.locator_params('x',nbins=10)
ax.locator_params('y',nbins=8)
plt.plot(x_data,y_data)
plt.show()
def DrawTwoChroms(chroms1, chroms2, fitfun): # 画2幅图,左边是旧种群,右边是新种群,观察平行的两幅图可以看出有没有差异
# 新建一个画布
figure = plt.figure()
# 新建一个3d绘图对象
ax1 = figure.add_subplot(1,2,1,projection='3d')
ax2 = figure.add_subplot(1,2,2,projection='3d')
# 生成x, y 的坐标集 (-2,2) 区间,间隔为 0.1
x = np.linspace(-2.9, 12.0, 20)
y = np.linspace(4.2, 5.7, 18)
# 生成网格矩阵
X, Y = np.meshgrid(x,y)
# 定义x,y 轴名称
plt.xlabel("x")
plt.ylabel("y")
# 设置间隔和颜色
#ax.plot_wireframe(X,Y,Z)
ax1.set_zlim(0, 40)
ax2.set_zlim(0, 40)
dechroms_x,dechroms_y = decode_v(chroms1)
fitness = fitfun(dechroms_x,dechroms_y)
ax1.plot_surface(X, Y, fitfun(X,Y), rstride=3, cstride=2, cmap="rainbow",alpha=0.65)
ax1.plot(dechroms_x,dechroms_y,fitness,'k.')
newdechroms_x,newdechroms_y = decode_v(chroms2)
fitness = fitfun(newdechroms_x,newdechroms_y)
ax2.plot_surface(X, Y, fitfun(X,Y), rstride=3, cstride=2, cmap="rainbow",alpha=0.65)
ax2.plot(newdechroms_x,newdechroms_y,fitness,'k.')
plt.show()
# 对比一下变异前后的结果
# DrawTwoChroms(chroms, newchroms, fun)
# 上述代码只是执行了一轮,这里反复迭代
np.random.seed(0)
population_x = np.random.uniform(-2.9, 12.0, 100) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
population_y = np.random.uniform(4.2, 5.7, 100)# 这次多找一些点
chroms_v = encode_v(population_x,population_y)
x_data=[]
for i in range(1001):
x_data.append(i)
y_data = []
for i in range(1000):
dechroms_x,dechroms_y = decode_v(chroms_v)
fitness = fun(dechroms_x,dechroms_y)
fitmax = np.max(fitness)
y_data.append(fitmax)
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
newchroms_v = Mutate(Select_Crossover(chroms_v, fitness))
if i % 300 == 1:
DrawTwoChroms(chroms_v, newchroms_v, fun)
chroms_v = newchroms_v
dechroms_x,dechroms_y = decode_v(chroms_v)
fitness = fun(dechroms_x,dechroms_y)
fitmax = np.max(fitness)
y_data.append(fitmax)
DrawTwoChroms(chroms_v, newchroms_v, fun)
print(len(y_data))
DrawMax(x_data,y_data)
print('函数的最大值为:')
print(np.max(fitness))
第六题代码来源:19级大数据三班 wcx