【李宏毅机器学习】Logistic Regression 逻辑回归（p11） 学习笔记

李宏毅机器学习学习笔记汇总
课程链接

---

Logistic Regression

Step 1: Function Set

逻辑回归和线性回归的step1的区别：

Step 2: Goodness of a Function

假设这批N个training data是从function定义的posterior probability所产生的
给出w和b，就给定了posterior probability，就可以计算某组w和b产生这N个training data的概率
最可能的w和b是 那组最大概率（最大化L(w,b)函数）产生这批training data的w和b，称作$w^{\ast }$和$b^{\ast }$

对公式进行转换：

两个伯努利分布的交叉熵，cross entropy代表这俩个分布有多么接近

如果这两个分布一样的话，KL散度是0，交叉熵等于真实分布的熵，是一个正常的熵，而不是0

逻辑回归和线性回归的step2的区别：

线性回归中的1/2方便求导去系数

Question：为什么我们不能用square error作为线性回归（在这里视频暂时未给出理由，记忆即可）

弹幕给出的回答：
一个先验是二项，一个先验是正态
两边本质都是似然，左边是二项的似然右边是高斯似然

Step 3: Find the best function

使用gradient descent来最小化$-\ln L(w,b)$

最后的化简结果：

w的更新取决于：

• learning rate
• $x_i$，来自于data
• ${\hat{y}}^n-f_{w,b}(x^n)$

${\hat{y}}^n$是目标
$f_{w,b}(x^n)$是现在模型的output

逻辑回归和线性回归的step3的区别：
公式是一模一样的，但是其中：

• 逻辑回归中的target(${\hat{y}}^n$)介于0-1（见step2的区别对比），f的取值也是介于0-1（见step1的区别对比）
• 线性回归中，target(${\hat{y}}^n$)可以是任何实数，output也可以是任何实数
• 但是这俩个的更新方式是一模一样的
  

这里提到实验：老师说的是直接找到最佳解（因为是线性回归，求导为零，找到一个解），然后再梯度下降

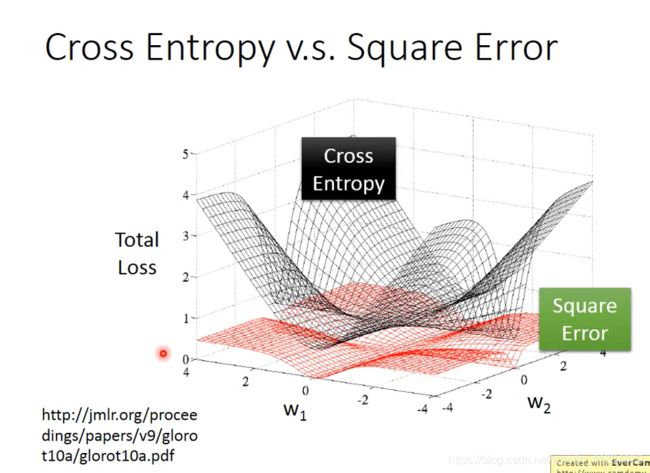
为什么逻辑回归不能用square error平方误差

无论距离目标远近，微分算出来都是0

把参数变化，对total loss作图：

• 交叉熵：距离目标越远，梯度越大
• square error：距离目标远的时候，微分很小，移动速度很慢，容易卡住

Discriminative vs Generative

• 逻辑回归是discriminative方法 判别式模型
• 用高斯分布来描述后验概率的方法是Generative方法，生成式模型

只要在做概率模型时候，把协方差矩阵共用，那么他们的模型是完全一样的，都是$P(C_1|x)=\sigma (w\ast x+b)$

下图左右两边的w和b不是同一组的

进行计算，对于NB来说，P<0.5，这组testing data（x1=1,x2=1）属于class2，而不是class 1，与认知相反，是因为data数量太少了

生成式模型和判别式模型的差别在于：
生成式模型有做某些假设，假设data来自某些概率模型

• gm模型提前假设，包含的函数会受限，dm则包含更多可能，因此可以得到比较好的效果
• 朴素贝叶斯是生成模型 逻辑回归是判别模型

生成式模型的优势

• 如果training data很少，针对同一个问题，给判别式模型和生成式模型不同量的data：
  1、判别式模型，没有做任何假设，完全依靠data，他的performance变化量会受data量影响很大，data越多，error越小
  2、生成式模型，受data影响小，因为他本身会有一个假设/脑补，有时会无视data，遵从他的假设。
  3、所以在data数量比较小的时候，生成式模型可能会赢过判别式模型。只有在数量增加时候，判别式模型才可能赢过生成式模型。

• 生成式模型，对于含有噪声的data，有了概率分布的假设，对于噪声可以更加鲁棒，忽视掉有问题的data

• 在判别式模型中，是假设了一个后验概率，然后去找后验概率的参数，但是生成式模型中把公式拆成先验概率和class-dependent probability类相关的概率两个部分，这样是有好处的，他们两个可以是来自不同的来源。（计算先验概率，某一句话被说出来的概率，所以语音辨识中，未必需要声音data，可以从网上爬一些数据，来计算这个先验概率，这就是language model。语音辨识其实是一个生成式模型。先验概率使用文字data来处理，class-dependent部分才需要声音data处理）

• 朴素贝叶斯是生成模型 逻辑回归是判别模型

Multi-class Classification

做完softmax后，output为0-1，且求和为1

softmax，对最大的值做强化，将大的和小的之间的差别做强化。

要计算y和$\hat{y}$的cross entropy，$\hat{y}$也要是一个概率分布，才可以算cross entropy，如何计算呢？

不可以假设class1是1，class2是2，class3是3：
因为这样会隐含class1和class2近，class2和class3近，而class1和class3较远，这样是不对的

最小化cross entropy来自于极大似然，在多个class情况下，依然一模一样。

Limitation of Logistic Regression 逻辑回归的限制

逻辑回归无法对下面的例子进行分类

因为逻辑回归的两个class之间的boundary是一条直线

所以，如果要坚持使用逻辑回归的话，可以用下面这种方法——Feature Transformation
前面的$x_1$，$x_2$的feature定的不好，可以转化一下，找一个好的feature space，从$x_1$，$x_2$ 到$x_1^{\prime }$，$x_2^{\prime }$

对于线性回归和的logistic回归的理解:

1. 其实主要原因是分布问题，在前面的线性回归里面，其分布主要是为高斯分布, 而在logistic里面的分布为 伯努利分布
2. 在线性回归中，同样用最大似然估计去估计w和b的值，得到的结果其实是和用square error (最小二乘)是一样的
3. 在logistic 回归中，因为估计的是伯努利分布，然后严格来说，也是可以用最大似然估计，但是数学家们发现用cross entropy 能更容易的找到希望的结果

那么如何让机器自己可以产生这种transformation呢？

把多个逻辑回归模型cascade 级联起来

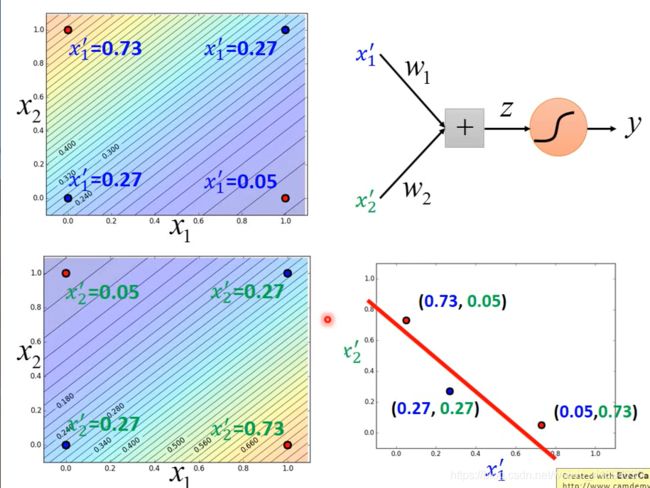
假设输入是$x_1$，$x_2$，有一个逻辑回归模型，

• 对$x_1$，$x_2$分别乘以一个权重，然后求和得到$z_1$，经过sigmoid 函数，output就是新的transform的第一维$x_1^{\prime }$；
• 对于另外一个逻辑回归模型。对$x_1$，$x_2$ 分别乘以另外一组权重，然后求和得到$z_2$，经过sigmoid函数，得到transform后的另外一维$x_2^{\prime }$，
• 如果把$x_1$，$x_2$经过这俩个逻辑回归的transform，得到$x_1^{\prime }$和$x_2^{\prime }$，而在这个新的transform上，class1和class2是可以用一条直线分开的，只需要再接上另外一个逻辑回归模型，input是$x_1^{\prime }$和$x_2^{\prime }$，$x_1^{\prime }$和$x_2^{\prime }$是每一个example的feature，根据这俩个新的feature就可以把class1和class2分开，
• 所以前面两个逻辑回归模型做的工作就是feature transformation，随后再由后面的逻辑回归模型来进行classification分类

可以调整蓝色/绿色逻辑回归的权重参数，让他的后验概率的output分别像图中颜色分布

有了前面这俩个逻辑回归后，就可以把input的数据做transform，得到另外一组feature，$x_1^{\prime }$和$x_2^{\prime }$

把多个逻辑回归模型相互连接起来，变得powerful，并且把每个逻辑回归模型赋予一个新的名字“Neuron”，把串起来之后组成的network叫做Neural Network，进入Deep Learning！妙啊！！！