【C/C++ & 汇编语言 & Verilog】越界截断——数据越界问题的多角度分析
0 前言
0.1 讨论层级和范围
- 讨论层级
- 计算机底层:硬件层次与汇编指令层次
- 信息与二进制位
- 讨论范围
- 信息的存储与运算在汇编语言与Verilog HDL中的联系与区别
- 事实上,数据越界截断问题,在计算机体系的任何层次,都可能发生,并且他们遵循的法则基本是一致的
0.2 其他说明
- 信息与数据,本质上来讲没有区别,信息就是数据,数据就是信息。为方便起见,在本文中,全部都称数据。
- 数据越界问题的分析,在实际应用中有以下用途
- 在一开始设计的时候避免越界问题的发生
- 在发生错误的时候有能力分析出其原因
1 一个概念
越界丢失法则:超过存储能力的数据,会被截断,从而导致丢失,也可以称为越界截断。
这就好比,一个水桶一旦装满水,再灌水会溢出来,溢出的水就是丢失了
1.1 越界截断
我们知道,数据在计算机中是以二进制信息存储的,即一串一串的二进制数
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| … |
对于上图所示的,是两个8位的二进制位串。
下面将通过演示说明,什么是越界截断,对于8个二进制位来说,所能表示的最大数据就是8位全部是1:
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|
如果再给这个数值加1,那么就会数值就变成:
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
这是9位二进制数,但实际上计算机只能存储8位,因此超过其所能承受的范围,最高位的1将会被截断,从而造成数据丢失:
| 被截断 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
也就变成了:
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
这就是数据的越界截断。
有些读者可能会误以为越界丢失就是归零,因此我再举一个例子,以消除误解。
对于8个二进制位来说,如果给他施加了达到10个二进制位的数字:
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
那么它的最高两位将会丢失
| 被截断 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
也就变成了:
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
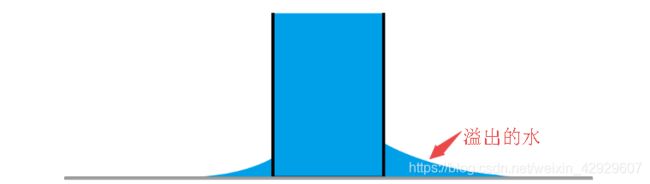
1.2 越界截断建模——水溢出模型
数据的越界丢失,就好比水桶满了,多出的水会溢出,但是水桶的水并不会消失,只是多出来的水丢失了。

1.3 补充概念——溢出
当数据发生越界,超出了容器容纳范围时,我们称发生了溢出
2 两个方向
对于越界截断现象,有两个考虑的方向。
2.1 数据的存储——水桶储水模型
2.2 数据的运算——水处理模型
信息的运算是指,对传输过来的数据,进行运算(加、减、乘、除……),也就是数据的处理过程
就好比污水经过处理厂变成了净水
亦或者是一桶水倒入另外一桶水中,这样的模型都是合理的,能够帮助你理解这一过程
3 三个过程
对于越界截断现象,一般会发生在三个过程中。
3.1 初始量:设初值
包含数据类型、标识符的设定,以及赋初值的过程
3.1.1 Verilog
在Verilog语言中,初始化的方式如下
reg a = 1'b1;
reg b = 123;
reg c;
c = 1'b0;
- 对于a和c来说,一个二进制位存储一个二进制数,这是标准的
- 对于b来说,显然数据越界了,Verilog会执行越界丢失操作,留下没越界的数字
- 123用二进制表示是:0111_1011
- 因此留下最后一位1,其余高位全部丢失
3.1.2 汇编语言
以8086CPU中16位寄存器AX为例,说明数据的初始化问题
mov AX,11H // ①
mov AX,1000001H // ②
- 对于①,将它显然正确
- 对于②,明显越界,这是错误的指令,注意,是错误,可能不会被容错直接报错
3.1.3 C/C++等高级语言
int a = 1000100010000;
int b = 100;
问题:为什么会显示右侧这一串数字?C++是怎么运行出来的?
在回答这个问题之前,先来学习一下延展知识。
3.1.3.1 延展阅读1:VS C++ 的内存查看方法
【VS C++ 2010】查看内存的方法详解
学习完之后,再继续往下进行
以下面的代码为示例:
int main()
{
int a = 100;
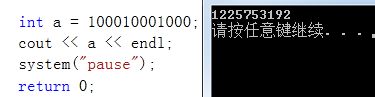
int b = 100010001000;
cout << "a = " << a << " " << &a << endl;
cout << "b = " << b << " " << &b << endl;
system("pause");
return 0;
}
以下,我们都需要使用刚刚学到的知识,查看内存的情况
(1)对于正数
①不越界的正数
对于int a = 100;,显然是不越界的,其内存情况为
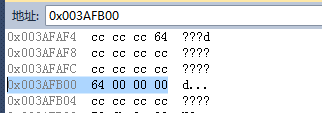
这一点没什么好说的
- a的类型为int
- 数值为100(十进制),被解释为数字100
- 存储为二进制位串
- 显示为0x64(十六进制的64)
②越界的正数
对于十进制数据 1000_1000_1000,其十六进制为:17 49 0F 82 68
| 17 | 49 | 0F | 82 | 68 |
|---|
由越界截断可得,被保留下来的为:49 0F 82 68
| 被截断 | 49 | 0F | 82 | 68 |
|---|
我们查看内存来验证一下
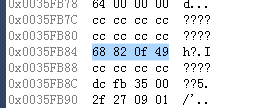
内存上的存储的确是这样,将其换算为十进制,就是我们的输出结果了
![]()
(2)对于负数的越界
3.1.3.2 延展阅读2:补码的使用
补码转换人工求法【非常没必要,计算机要做的事情为什么要人来做?不过做考试题还是有必要的……】:
- 求负数绝对值的原码后减一【这个减一就很蠢,补码的使用就是为了避免减法,你居然用减法来避免减法……,但是做考试题确实比用反码的方法更快】
- 对上述结果全部取反
对于负数,计算机以补码形式来存储的本质
对于负数:
- 计算机先将其转换为补码形式
- 再进行存储,如果越界,则会发送越界截断
①不越界的负数
直接以补码形式存储
②越界的负数
先存储为补码,然后越界截断,然后再存储起来
3.1.4 小结
我通过三种语言的描述,来为你传到这样的信号:
- 不同语言对于越界问题的处理方式是不同的,这是显而易见的,他们所处的计算机系统层次不一样,抽象程度也不一样
- 毫无疑问,在赋初值的时候就造成越界,这是设计的失败,这是不可容忍的错误
总之,不要越界(后面的小节会讲解它也是双刃剑,可以**“变废为宝”**)
3.1.4.1 延展阅读3:在边界内做事情
待完善部分,敬请期待
3.1.4.2 优化模型——水桶的水不能溢出
对于水桶储水模型,请回看2.1节的内容,这里通过几张图来展示几种可能的情况
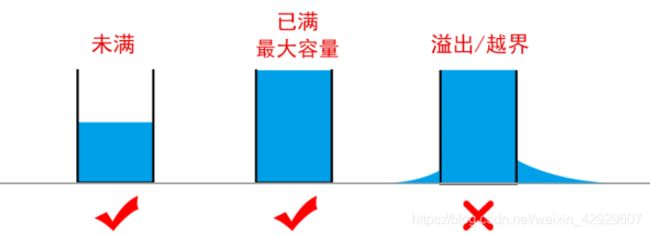
3.1.4.3 一句话总结:做事不能越界
3.2 过程量:做运算
对于运算之后造成的越界问题,参考3.1.3节中的问题部分的解答即可
3.2.1 数学运算(加减乘除……)
不管是高级语言,还是汇编语言,在进行数学运算的时候都可能产生越界的问题——两个数字都没有越界,但是相加之后越界了
设计者一定要考虑并且避免这些问题的发生,否则可能会引发错误。
3.2.2 数据类型的强制转换
3.2.2.1 手动强制转换
数据的强制转换也可能引发错误,比如:在java中,将int类型的数字转换为byte类型,由高向低转换,就可能引起数据的丢失。
例如下列Java代码
int a = 300;
byte b = (byte)a;
System.out.println(b);
输出为:
![]()
原因分析:
对于原数字,被保存为0x12C(十六进制前缀为“0x”),强制转换为byte类型,则会发生越界截断,将最高位的1截断,变成了0x2C,也就是十进制的44
3.2.2.2 自动强制转换
另外,在C/C++、Java中,有一类二元运算符,比如
- +=
- -=
- *=
- /=
例如x += y,它的本质是x = x + y,由于y的数据类型并不确定,因此可能会产生错误,比如:
int x = 3;
x = x + 3.5;
这是不被允许的,x + 3.5是float类型,不能直接赋值给int类型,这时候需要进行强制转换x = (int)(x + 3.5),得到的结果是6
对于上述二元运算符来说,这个强制转换是自动进行的
int x = 20;
x += 3.5;
对于第二条语句,并不等价于x = x + 3.5而是等价于x = (int)(x + 3.5)
3.3 结束量:得结果
3.3.1 直接输出
对于得到的结果,直接输出,那么就是越界丢失之后的结果,没什么好说的。
如果直接在输出函数的参数内进行运算,那么越界与否取决于实际的环境,看情况而定,数据的结果一定要在范围内!。
3.3.2 结果被保存到其他变量中
如果运算得到的结果被保存到了其他变量中,如果将大的数据,保存到小容器中,显然会越界
4 双刃剑——越界截断的利弊分析
4.1 避开弊端
从专业词语来说,越界丢失更适合称为越界截断,越界的部分将会被计算机截断,从而造成了丢失。

毫无疑问,数据的丢失是可怕的,因此,大多数情况下,尤其是程序员,要尽可能的避免发生越界截断。
4.2 坏事变好:应用越界截断——补码的使用
从哲学的角度来说,任何事情都有两面性,如果我们利用好越界截断,也能让它发挥巨大的作用。
计算机有加法器,但是它不擅长减法,于是
- 补码+越界截断
就完成了减法转换为加法这一壮举!
例如:45 + (-22) = 23
在计算机中,以补码形式存储,用补码进行加减
45的补码:
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
|---|
-22的补码:
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
|---|
补码相加:
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
|---|
发生越界截断:
| 被截断 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
|---|
得到:
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
|---|
也就是23的补码
**但是,务必注意:**使用补码进行运算,运算结果也一定要在范围内,否则依然是错误。
5 注意事项:先确定正确的界限,才能分析越界截断
比如下面这个例子,如果你把它的界限弄错,那么你可能会得到错误的结果。
char a = 100;
char b = 28;
char c = a+b;
cout << dec << (int)c << endl;
unsigned char d = a+b;
cout << dec << (int)d << endl;
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
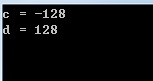
但是,同样是char类型,一个是有符号数,一个是无符号数,输出的结果却不一样。
这是因为
- 对于有符号数来说,它的界限的7位,因为要除去符号位
- 对于无符号数来说,它的界限是8位,不需要除去符号位
说到这里,你也就明白,数据的界限是讨论越界截断的前提。
因此设计者要综合考虑很多问题,这也是计算机科学家的基本素养。
6 综合阐述
- 任何计算机程序都是由各种数据构成的
- 各种数据又拥有不同的数据类型
因此:数据只要在对应数据类型的范围内,就不会发生错误。
最终结果就是,保证数据在数据类型的范围内运行即可,对于补码运算而言,中间过程发生越界是没有问题的,但是结果不能越界,上面一大堆分析完全可以不用看(不要打我……分析有助于你未来思考更深入的问题,光记住结论是走不远的)。
7 延展阅读汇总
待补充