神经网络

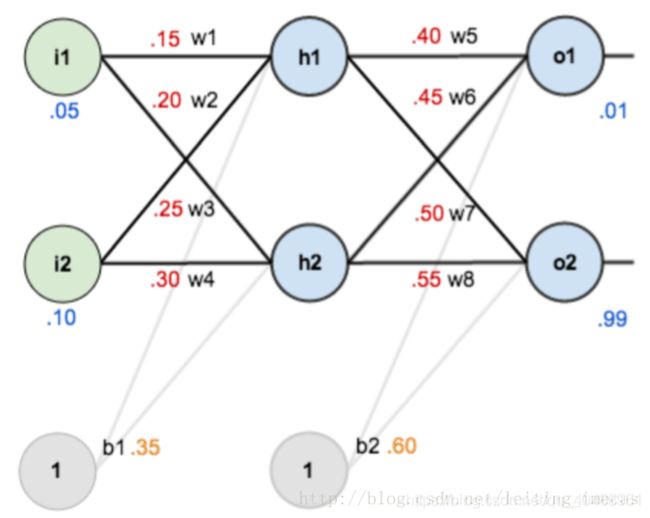
1）前向计算误差：

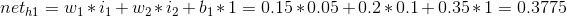
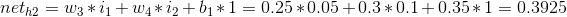
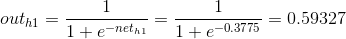
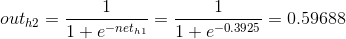
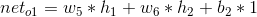
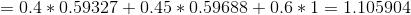
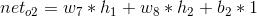
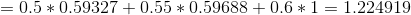
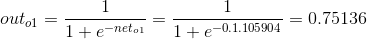
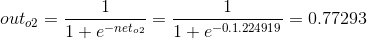
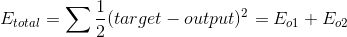
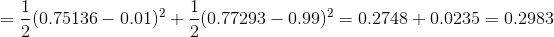
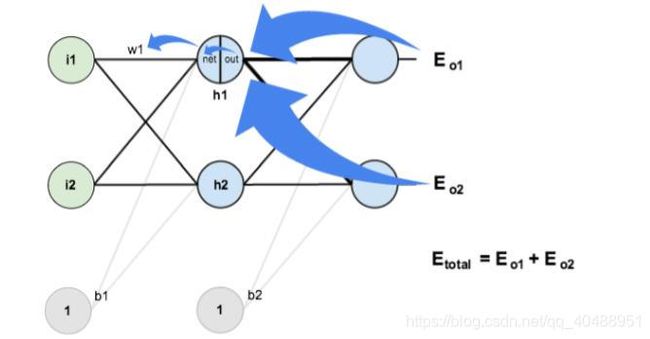
2）向后传播

1、更新W5参数

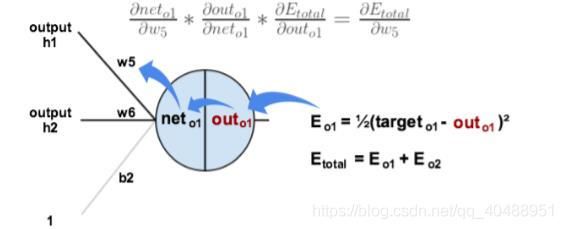
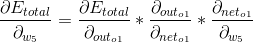
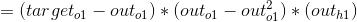
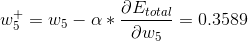
2、更新W1参数

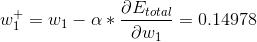
import numpy as np
import h5py

def load_dataset():
    train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:])  # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:])  # your train set labels

    test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:])  # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:])  # your test set labels

    classes = np.array(test_dataset["list_classes"][:])  # the list of classes

    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

def predict(w, b, X):
    Y_prediction = np.zeros((1, X.shape[1]))
    w = w.reshape(X.shape[0], 1)   #(12288, 1)
    # 计算结果
    A = 1 / (1 + np.exp(-(np.dot(w.T, X) + b)))
    for i in range(A.shape[1]):
        if A[0, i] <= 0.5:
            Y_prediction[0, i] = 0
        else:
            Y_prediction[0, i] = 1
    return Y_prediction


# 1、读取样本数据
train_x, train_y, test_x, test_y, classes = load_dataset()
# print("训练集的样本数: ", train_x.shape[0])  #209
# print("测试集的样本数: ", test_x.shape[0])  #50
# print("train_x形状: ", train_x.shape)  #(209, 64, 64, 3)
# print("train_y形状: ", train_y.shape)  #(1, 209)
# print("test_x形状: ", test_x.shape)  #(50, 64, 64, 3)
# print("test_x形状: ", test_y.shape)  #(1, 50)

# 输入数据的形状修改以及归一化
train_x = train_x.reshape(train_x.shape[0], -1).T  #将图像拉成一维，转置后每列代表一副图，每个元素为灰度值
# print(train_x.shape)  #(12288, 209)
test_x = test_x.reshape(test_x.shape[0], -1).T
# print(test_x.shape)  #(12288, 50)
train_x = train_x / 255.
test_x = test_x / 255.

# 2、模型训练以及预测
# 初始化参数
w = np.zeros((train_x.shape[0], 1))  #(12288, 1)
b = 0
num_iterations = 2000
learning_rate = 0.005

# 梯度下降
for i in range(num_iterations):
    # 梯度更新计算函数
    m = train_x.shape[1]  #209
    # 前向传播
    A = 1 / (1 + np.exp(-(np.dot(w.T, train_x) + b)))  #(1, 209)
    # 计算损失
    cost = -1 / m * np.sum(train_y * np.log(A) + (1 - train_y) * np.log(1 - A))

    # 反向传播
    dz = A - train_y
    dw = 1 / m * np.dot(train_x, dz.T)   #(12288, 1)
    db = 1 / m * np.sum(dz)

    # 按照梯度下降公式去计算
    w = w - learning_rate * dw   #(12288, 1)
    b = b - learning_rate * db

    if i % 200 == 0:
        print("损失结果 %i: %f" % (i, cost))
        print(b)

Y_prediction_train = predict(w, b, train_x)
Y_prediction_test = predict(w, b, test_x)

# 打印准确率
print("训练集准确率: {} ".format(100 - np.mean(np.abs(Y_prediction_train - train_y)) * 100))
print("测试集准确率: {} ".format(100 - np.mean(np.abs(Y_prediction_test - test_y)) * 100))
------------------------------------------
损失结果 1600: 0.159305
-0.01619503271238927
。。。。。。

损失结果 1800: 0.146542
-0.016079553977362767
训练集准确率: 99.04306220095694 
测试集准确率: 70.0