codeforces 619（Div.2）E. Nanosoft

题意：给定一个$n\ast m,(1<=n,m<=500)$的只含有四种颜色标识的矩阵，定义合法矩阵为：

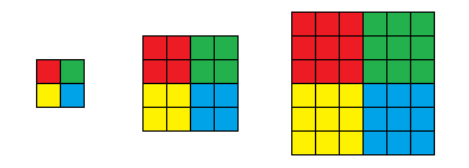
类似这样的四个块相同，且每个块内颜色一致，颜色分布位置也与之一致。
接下来有$3e5$次询问，每次给出$(r1,c1),(r2,c2)$，询问以$(r1,c1)$为左上角，$(r2,c2)$为右下角的区域内最大的合法子矩形的面积是多少。

我的思路：
四个数组预处理出每种颜色的二维前缀和，然后处理出以$(i,j)$为左上角的每个点可以形成的最大矩形，对于每个点二分长度，check即可。接下来对于询问我就不会做了。。。。降不下来复杂度。
于是参考了题解：
题解的做法也是对于每个点计算最大矩形面积，但他的val[i][j]表示的是以(i,j)为合法矩形最靠里的那个点围绕该点形成的最大矩形。
然后预处理二维RMQ。
接下来的mid指的是**合法矩形块（合法矩形拆成四个小块）**的长度
那这样的话，对于询问，可以二分合法矩形块的长度mid，如果查到范围在$(r1+mid-1,c1+mid-1),(r2-mid,c2-mid)$内的最大值是大于等于4midmid则说明可能为答案。
因为预处理时处理出来的是最中心的点，故以该点为中心能构造出来的合法矩形的长度肯定在$[0,val[i][j]]$之间，故只要最大值满足大于等于4midmid，那么就说明肯定可以构造出来一个长度是mid的合法矩形。

#include
using namespace std;

typedef long long ll;
const int maxn=509;

//0 r 1 g 2 y 3 b;
int col[maxn][maxn][4];//前缀和;

char s[maxn][maxn];

bool check(int r1,int c1,int len,int i){
    int r2=r1+len-1,c2=c1+len-1;
    //cout<
    return col[r2][c2][i]-col[r1-1][c2][i]-col[r2][c1-1][i]+col[r1-1][c1-1][i]==(r2-r1+1)*(c2-c1+1);
}

bool check(int i,int j,int len){
    int r1=i-len+1,c1=j-len+1;
    return check(i-len+1,j-len+1,len,0)&&check(i-len+1,j+1,len,1)&&check(i+1,j-len+1,len,2)&&check(i+1,j+1,len,3);
}
int val[maxn][maxn][11][11];//RMQ;

void init(int n,int m){
	int up1=log2(n)+1,up2=log2(m)+1;
	for(int l1=0;l1<up1;l1++){
		for(int l2=0;l2<up2;l2++){
			if(!l1&&!l2) continue;
			for(int i=1;(i+(1<<l1)-1)<=n;i++){
				for(int j=1;(j+(1<<l2)-1)<=m;j++){
					if(l2)val[i][j][l1][l2]=max(val[i][j][l1][l2-1],val[i][j+(1<<(l2-1))][l1][l2-1]);
					else val[i][j][l1][l2]=max(val[i][j][l1-1][l2],val[i+(1<<(l1-1))][j][l1-1][l2]);
                    //cout<
				}
			}
		}
	}

}

int ask(int x1,int y1,int x2,int y2){
	int p=log2(x2-x1+1),q=log2(y2-y1+1);
	int ans=0;
	ans=max(val[x1][y1][p][q],val[x1][y2-(1<<q)+1][p][q]);
	ans=max(ans,max(val[x2-(1<<p)+1][y1][p][q],val[x2-(1<<p)+1][y2-(1<<q)+1][p][q]));
	return ans;
}


int main(){
    int n,m,q,r1,c1,r2,c2;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;++i){
        scanf("%s",s[i]+1);
        for(int j=1;j<=m;++j)
            if(s[i][j]=='R') ++col[i][j][0];
            else if(s[i][j]=='G') ++col[i][j][1];
            else if(s[i][j]=='Y') ++col[i][j][2];
            else ++col[i][j][3];
    }
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
            for(int k=0;k<4;++k)
                col[i][j][k]+=col[i-1][j][k]+col[i][j-1][k]-col[i-1][j-1][k];
    for(int i=1;i<n;++i)
        for(int j=1;j<m;++j){
            if(s[i][j]!='R') continue;
            int l=1,r=min(min(i,j),min(n-i,m-j)),mid;
            //cout<
            while(l<=r){
                mid=l+r>>1;
                if(check(i,j,mid)) l=mid+1;
                else r=mid-1;
            }
            val[i][j][0][0]=r*r*4;
            //cout<
        }
    init(n,m);
    while(q--){
        scanf("%d%d%d%d",&r1,&c1,&r2,&c2);
        int l=1,r=min(r2-r1+1,c2-c1+1)/2,mid;
        while(l<=r){
            mid=l+r>>1;
            if(ask(r1+mid-1,c1+mid-1,r2-mid,c2-mid)>=4*mid*mid) l=mid+1;
            else r=mid-1;
        }
        printf("%d\n",r*r*4);
    }

    return 0;
}