Java实现：交换排序之快速排序(Quicksort)、(基础、二路、三路快速排序)

1、简单快排

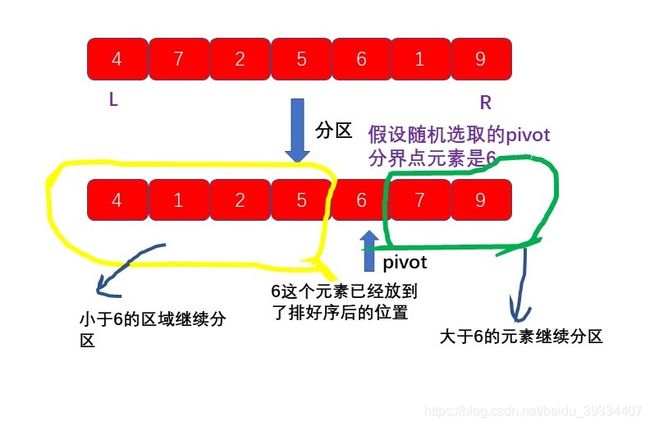
• 所谓快速排序，利用的是一种“分而治之”的思想，有点像归并排序，但是还是有点区别的；
• 快排思想是这样的：待排序数组中下标从l(左边)到r(右边)之间的一组数据，我们选择其中任意一个元素作为分区点pivot，然后这组数据中大于分区点元素的全部放到它的右边，小于它的全部放到左边，此时这组数据中，这个pivot元素以及排到了它将要排序后的位置；然后它左右两边的两组数据接着以这种方式选分区点、分割；知道最后每组数据中仅剩下一个元素，此时最开始要排序的数组已经排好序；
• 这就是“分而治之”的思想，也是递归的思想；
  1、先来实现递归的代码部分，解释一下代码，就是这个方法实现的功能：接收到一组数据，两个参数，左边界L和右边界R，我们得知道需要排序的区域，当然这样也是可以实现无序数组的部分内容排序：

private static void quickSortInternal(int[] array,int l,int r){
        if (l >= r){
            return;
        }
        //q就是当前的分区点pivot,partion()方法就是找到分区点并且返回这点的下标，下标为q
        int q = partition(array,l,r);
        //下面进行递归分区，下标左右两边的数组继续寻找pivot分区点，继续划分；
        //递归就是继续调用本方法，传入新的数组以及分区；
        quickSortInternal(array,l,q-1);
        quickSortInternal(array,q+1,r);

    }

2、下面是partioon()方法，分区函数，此方法作用就是随机选取一个元素作为分区点pivot，然后进行分区，就是将小的元素往前放，大的元素往后放；这里要注意一点，分区方法的操作，全部是在本数组中进行的，原地完成分区操作；
先来看看代码：

/**
     *  分区点
     * @param array 传入的数组
     * @param l  左边界
     * @param y  右边界
     */
    private static int partition(int[] array,int l,int r){
        //每次以第一个元素为分区点进行快排，
        //对一个近乎有序并且特别大的数列进行快排会发生栈溢出
        //因为栈内存不够用，递归不下去了；
        int randomIndex = (int) ((Math.random()*(r-l+1))+l);//获得一个随机的下标，随机数不超过数组的长度-1
        swap(array,l,randomIndex);//交换第一个元素跟随机的这个元素，这个swap方法自己写的
        int v = array[l];
        int j = l;
        int i = l + 1 ;
        for (;i <= r;i++){
            if (array[i] < v){
                swap(array,j+1,i);
                j++;
            }
        }
        swap(array,l,j);
        return j;
    }

画个图来解释一下代码，代码中的三个指针下标：L,i,j,(R不必解释，就是一个临界点)
如图所示：

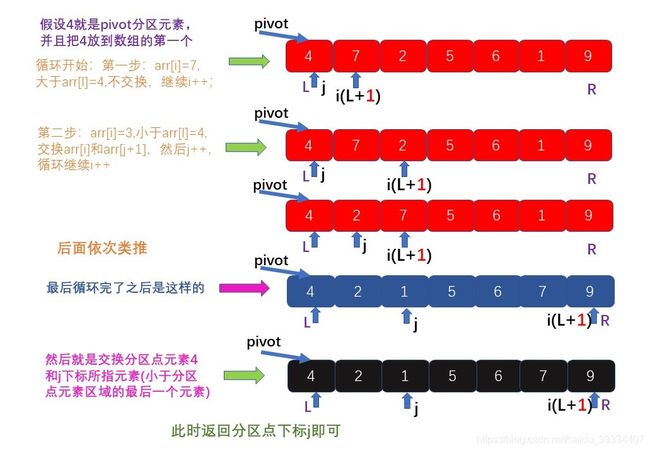
• 代码中有一个要注意的点，就是j一直指向小于分区点元素区域的最后一个元素，而且在分区的过程中，分区点元素一直在数组第一位，直到for循环最终进行完，就是j最终增加完了之后，从j元素的下一个元素开始全都是大于分区点元素的数据；此时交换j跟L所指向的pivot元素，此时分区点元素已经找到，并且已经分区完成，然后返回分区点元素的下标j;
• 代码中还有一个优化点，一开始partion 分区选择pivot元素的话都是当前元素的第一个元素，可是当待排序元素近乎有序时，若选取的基准值恰好为最大值，此时分层退化成O(n),此时快排的时间复杂度退化为O(n^2);所以我们做一个小的优化，每次从待排序的
  数组中随机选取一个元素作为pivot基准值，这样可以保持均衡性；解决这个问题；

2、二路快排

首先简单说一下二路快速排序法的由来

如果数字集合中的数字重复度非常高，包含大量重复的元素，那么也会出现这种情况，也会导致数组长度不均衡，相同的元素都会放到分区点右边，分层下来后右边的元素会越来越多，此时分层下来的结果近乎n层，快排退化为O(n^2)；

为了解决这种情况，我们想出了下面这种方法：

就是把相等的两个元素均衡的分配到基准值两边；这样的话分层下来后左右两个数组中相等的元素均衡分布；

那么如何做呢：

跟前面的简单快排不同，这次我们增加了一个遍历数组的指针，两个指针，就是两个下标，一个是 i 从前往后遍历，另一个是 j 从后往前遍历，当i遇到 >pivot 的时候停下，等 j ，然后j遇到 < pivot 的时候停下并且与停下来的 i 所指向的元素交换；然后再次开始遍历；结束条件 j < i;

下面先看一下我自己画的演示图：

Java代码实现partion()分区方法：

private static int partition2(int[] data,int left,int right){
//左下标跟右下标刚开始都分别指向小于pivot区域
//的前一个位置和大于pivot区域的后一个位置；
//当遍历开始后，交换开始后，i一直指向小于pivot区域的最后一个元素，
//j一直指向大于pivot的第一个元素；
        int i = left+1;
        int j = right;
        int value = data[left];
        while(i <= j){
            while(data[i] < value){
                i++;
            }
            while(data[j] > value){
                j--;
            }
            if (i > j){
                break;
            }
            swap(data,i,j);
            i++;
            j--;
        }
        swap(data,left,j);
        return j;
    }

• 这里解释一下最后为何交换的是 j 为下标的元素，因为最外层 while 循环停止的时候，就是当 j 小于 i 的时候，不论什么情况都是j指向小于基准值元素的最后一个元素，所以直接交换基准值跟该元素，恰好把基准值放到了指定位置；

3、三路快排

• 相比二路快排，当出现大量等于分区点值的时候，增加一个区域，等于区域，也就是说一共三个区域，“>”、"="、"<"三个区域；三路快排再一次减少了耗时；因为少了很多交换次数；
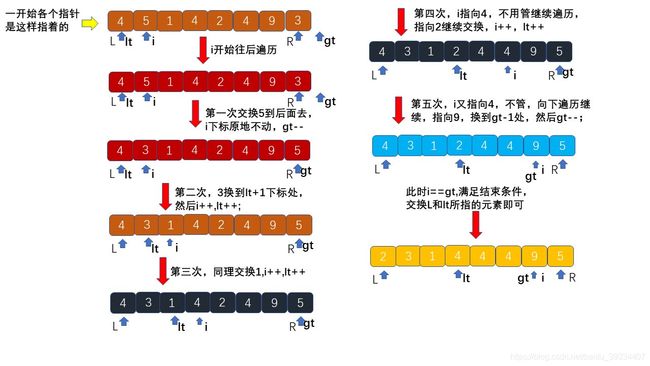
• 三路快排的思想跟双路优点区别，当递归处理的时候，遇到等于v的元素直接不用管
  只需要处理小于v，大于v的元素就好了；
• 自己总结了一下，因为是原地排序，所以很好理解，一共三个指针，lt,i,gt,，，，lt永远指向小于pivot区域的最后个元素，，，gt永远指向大于pivot区域的的第一个元素，，，i一直向后遍历元素；刚开始lt指向小于v区域的前一个位置，即初始位置，每当i遍历到一个小于v的元素的时候，交换lt+1元素跟i的元素，然后i指向下一个元素；同样gt，初始指向大于v区域的前一个位置；每当i遍历到一个大于v的元素的时候交换gt-1跟i的元素，但是此时注意，因为交换到i位置的元素不知道跟v谁大小，所以此处不能i++；同样的道理，当i遍历结束后，lt这个从后往前遍历的指针一定是指向小于v区域的最后一个元素，此时交换基准值元素跟lt处的元素，然后返回gt,即指定位置的元素的下标；

自己画的示意图

实现代码：

/**
     *  分区点
     * @param array 传入的数组
     * @param l  左边界
     * @param y  右边界
     */
    private static int partition3(int[] array,int l,int r){
        //三个指针，lt永远指向小于pivot区域的最后个元素
        //gt永远指向大于pivot区域的的第一个元素
        //i一直向后遍历元素；跟双路快排优点差别，双路快排是两个指针同时
        //分别从前向后、从后向前遍历；三路快排是三个指针，两个固定指向，一个从前向后遍历；
        int value = array[l];
        int lt = l;//刚开始lt指向小于v区域的前一个位置；即初始位置；
        int i = l+1;
        int gt = r+1;//同样gt后向前遍历，初始指向大于v区域的前一个位置；
        //下面开始遍历,从l+1处开始遍历
        while (i < gt){
            if (array[i] < value){
                swap(array,i,lt+1);
                lt++;
                i++;
            }else if(array[i] > value){
                swap(array,i,gt-1);
                gt--;
                //此处不能i++；因为当前i的元素是换回来的gt-1位置的元素
                //必须再次比较
                //前一个if入口的i++是因为当前i所指的元素就是换过来的小于
                //v的值，所以直接遍历下一个元素就行；
                // i++;
            }else{
                i++;
            }
        }
        //注意：这里的循环完成后，一定是gt指向小于v的最后一个区域；
        //所以这里可以直接交换l和gt的元素，然后返回gt 这个下标；
        swap(array,l,lt);
        return lt;
    }

4、快排总结

• 20世纪最重要的算法之一，也是基于分治思想；
• 时间复杂度：最好情况：O(n log n )；
  最坏情况：O(n^2);要排序的数列已经完全有序了；
• 稳定性：不稳定算法（若基准值为最后一个元素，5，4，3，2，6，1，5）；