算法设计与分析》第六周作业

《算法设计与分析》第六周作业

标签（空格分隔）： 课堂作业

姓名：李**
学号：16340114
题目：Median of Two Sorted Arrays（https://leetcode.com/problems/median-of-two-sorted-arrays/description/）

---

题目概要

给定两个有序的数列，找出两个数列归并之后的中位数。其实这道题就是“在两个有序数列中找第k小的数”的特殊情况。

思路

先来解决“在两个有序数列中找第k小的数”。一种很直观的思路就是把两个数列利用归并排序合起来，直接找中位数。这个方法很简单，但是算法复杂度是O(m + n)【数列1长度为m，数列2长度为n】，并不算很快。利用二分查找的思想可以更快地找到第k小的数。
　　我们先把两个数组各分成两组，并比较两个数组中间元素的大小关系，企图找到第k个数落在四段中的哪一段。可惜现实并没有这么理想，好在我们能排除第k个数不在四段中的哪一段。
　　
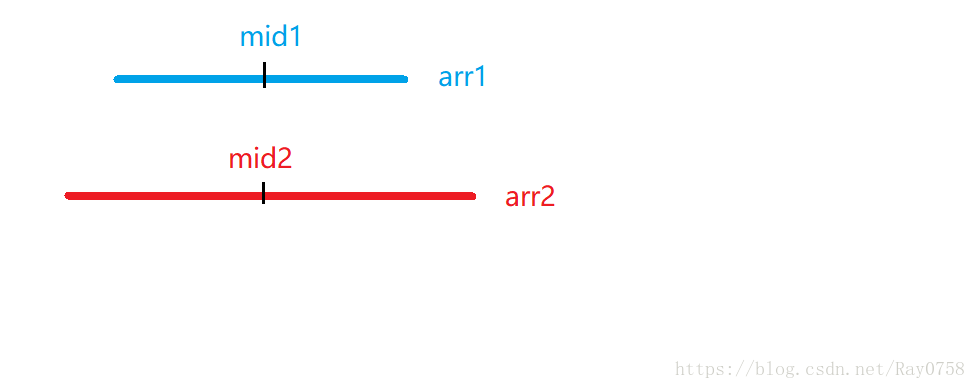
　　情况1：(m + n) / 2 < k 【说明第k个数在合并后的数列靠后半部分的位置】
　　　　（i）arr1[mid1] < arr2[mid2]
　　　　　　如图所示：数列1的中间元素小于数列2的中间元素时，数列1的前半部分是绝对在合并数列的前半部分的。下面是比较极端的情况:
　　　　　　(1)数列1的前半部分比数列2的前半部分都小，那这一部分是绝对排在合并数列的最前面的，这样的话可以将数列1的前半部分砍去。
　　　　　　
　　　　　　(2)数列1的前半部分仅小于数列2的中间元素，即使是这样数列1的前半部分也只能排在合并数列的前半部分，这部分也可以放心地砍去。
　　　　　　
　　　　　　(3)介于(1)与(2)两个极端之间的中间情况，这些情况中数列1的前半部分也是可以排除掉的。
　　　　（ii）arr1[mid1] >= arr2[mid2]
　　　　 　　交换arr1与arr2，重复（i）
　　情况2：(m + n) / 2 >= k 【说明第k个数在合并后的数列靠前半部分的位置】
　　和情况1的思路相似，这次是要把两个数列中的一个的后半部分砍去即可。
　　　　（i）arr1[mid1] < arr2[mid2]
　　　　 　　砍去arr2的后半部分
　　　　（ii）arr1[mid1] >= arr2[mid2]
　　　　 　　交换arr1与arr2，重复（i）

将对砍掉一半的数列与另一数列重复该操作，直到某一个数列完全被砍没了之后，第k个数自然就浮现了。
　　
得到寻找第k个数的方法后，找中位数就很简单了。
如果m+n是奇数，只需要找第(m+n)/2个数即可。
如果m+n是偶数，计算第(m+n)/2 - 1个数与第(m+n)/2个数的平均值即可。

具体实现

按照上述思路编写找第k个数的递归函数，basic case为其中一个数列为空，输出另一数列的第k个元素，递归过程按照上述四种情况进行，每次递归都通过传递vector的begin()和end()迭代器实现切分数组的效果，迭代的同时根据情况修改k的值(砍掉前半部分就将k减相应的长度，砍后半部分k值不变)。最后调用该找第k个元素的函数，找出中位数，完成！算法复杂度为O(log(m+n))

心得

感觉这个二分查找比第一周刚看这题时看的那个解法要好懂太多了，果然条条大路通罗马呀

源码：

#define mid1 ( (end1 - nums1) / 2)
#define mid2 ( (end2 - nums2) / 2)

class Solution
{
public:
    double findMedianSortedArrays(vector& nums1, vector& nums2)
    {
        if ( (nums1.size() + nums2.size()) % 2 == 1 )
            return kthSmallestNum( (nums1.size() + nums2.size()) / 2,
                                    nums1.begin(), nums2.begin(),
                                    nums1.end(), nums2.end() );
        else
            return (double)kthSmallestNum( (nums1.size() + nums2.size()) / 2 - 1,
                                    nums1.begin(), nums2.begin(),
                                    nums1.end(), nums2.end() ) / 2
                    +
                    (double)kthSmallestNum( (nums1.size() + nums2.size()) / 2,
                                    nums1.begin(), nums2.begin(),
                                    nums1.end(), nums2.end() ) / 2;

    }

    int kthSmallestNum(int k, vector::iterator nums1, vector::iterator nums2,
                              vector::iterator end1, vector::iterator end2)
    {
        if (nums1 == end1)
            return *(nums2 + k);
        if (nums2 == end2)
            return *(nums1 + k);

        if (mid1 + mid2 < k)
        {
            //the kth smallest number is in the second half
            if ( *(nums1 + mid1) < *(nums2 + mid2) )
            {
                //cut the first half of nums1
                return kthSmallestNum(k - mid1 - 1, nums1 + mid1 + 1, nums2, end1, end2);
            }
            else
            {
                //cut the first half of nums2
                return kthSmallestNum(k - mid2 - 1, nums1, nums2 + mid2 + 1, end1, end2);
            }
        }
        else
        {
            //the kth smallest number is in the first half
            if ( *(nums1 + mid1) < *(nums2 + mid2) )
            {
                //cut the second half of nums1
                return kthSmallestNum(k, nums1, nums2, end1, nums2 + mid2);
            }
            else
            {
                //cut the second half of nums2
                return kthSmallestNum(k, nums1, nums2, nums1 + mid1, end2);
            }
        }
    }
};