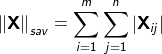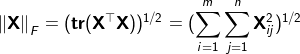qingdaobaibai

《Convex Optimization》附录A数学背景

附录A 数学背景

1. 范数

1.1 内积与夹角

n维向量内积： $<\mathbf{x},\mathbf{y}> = \mathbf{x}^{\top} \mathbf{y} = \sum_{i=1}^{n} \mathbf{x}_i \mathbf{y}_i$

m×n维矩阵内积： $<\mathbf{A}, \mathbf{B}> = \textbf{tr}(\mathbf{A}^{\top} \mathbf{B}) = \sum_{i=1}^{m} \sum_{j=1}^{n} \mathbf{A}_{ij} \mathbf{B}_{ij}$

向量(矩阵)夹角： $\angle (\mathbf{x}, \mathbf{y}) = \cos^{-1}(\frac{<\mathbf{x}, \mathbf{y}>}{\left \|\mathbf{x} \right \|_2 \left \| \mathbf{y} \right \|_2})$

Cauchy-Schwartz inequality： $\left | <\mathbf{x}, \mathbf{y}> \right | \leqslant \left \| \mathbf{x} \right \|_2 \left \| \mathbf{y} \right \|_2$ ，等号成立当且仅当向量x和y共线

1.2 常见范式（A.1.3）

向量范数

Lp-范数： $\left \| \mathbf{x} \right \|_p=(\left | \mathbf{x}_1 \right |^p + \cdots + \left | \mathbf{x}_n \right |^p)^{1/p}$

p=1、2、∞时比较常用

L1-范数（绝对值和范数）： $\left \| \mathbf{x} \right \|_1=\left | \mathbf{x}_1 \right | + \cdots + \left | \mathbf{x}_n \right |$

L2-范数（Euclidean范数）： $\left \| \mathbf{x} \right \|_2=(\left | \mathbf{x}_1 \right |^2 + \cdots + \left | \mathbf{x}_n \right |^2)^{1/2}$

L∞-范数（Chebyshev范数）： $\lim_{p \to +\infty}\left \| \mathbf{x} \right \|_p=\lim_{p \to +\infty} (\left | \mathbf{x}_1 \right |^p + \cdots + \left | \mathbf{x}_n \right |^p)^{1/p} = \max\{\left | \mathbf{x}_1 \right | , \cdots , \left | \mathbf{x}_n \right |\}$

最后一个极限是数学分析的知识，可用夹逼法证明。

P-二次型范数：若P为正定矩阵，则 $\left \| \mathbf{x} \right \|_\mathbf{P}=(\mathbf{x}^{\top} \mathbf{P} \mathbf{x})^{1/2} = \left \| \mathbf{P}^{1/2} \mathbf{x} \right \|_2$

这是十分常用的范数，可以方便的表示很多量，椭圆也可以用它简洁的表示。

矩阵范数

绝对值和(sum-absolute-value)范数： $\left \| \mathbf{X} \right \|_{sav}=\sum_{i=1}^{m} \sum_{j=1}^{n} \left | \mathbf{X}_{ij} \right |$

Frobenius范数： $\left \| \mathbf{X} \right \|_{F}=(\textbf{tr}(\mathbf{X}^{\top} \mathbf{X}))^{1/2}=(\sum_{i=1}^{m} \sum_{j=1}^{n} \mathbf{X}_{ij}^2 )^{1/2}$

绝对值最大(maximum-absolute-value)范数： $\left \| \mathbf{X} \right \|_{mav}=\lim_{p \to +\infty}(\sum_{i=1}^{m} \sum_{j=1}^{n} \left | \mathbf{X}_{ij} \right |^p )^{1/p} =\max \{ \left | \mathbf{X_{ij}} \right | | i = 1, \cdots, m, j = 1, \cdots, n \}$

与向量范数相似，对应为p取1、2、∞的情况。

算子范数（A.1.5）

定义：在范数a $\left \| \cdot \right \|_a$ 和范数b $\left \| \cdot \right \|_b$ 意义下，矩阵 $\mathbf{X} \in \mathbb{R}^{m \times n}$ 的算子范数为

$\left \| \mathbf{X} \right \|_{a,b} = sup \{ \left \| \mathbf{X} \mathbf{u} \right \|_a | \left \| \mathbf{u} \right \|_b \leq 1 \}$

这种较为一般的定义往往是不常用的，这里举了几个最常用的例子，仍分别对应1、2、∞三种情况。

当a=b=1时，

最大列和(max-column-sum)范数： $\left \| \mathbf{X} \right \|_1 = \max_{j=1, \cdots, n} \sum_{i=1}^{m} \left | \mathbf{X}_{ij} \right |$

推导：记第j列列和最大，则令 $\mathbf{u}_j$ 为1，其余为0，易得此时取得最大值

当a=b=2时，

谱(spectral)范数： $\left \| \mathbf{X} \right \|_2 = \sigma_{\max}(\mathbf{X}) = (\lambda_{\max}(\mathbf{X}^{\top} \mathbf{X}))^{1/2}$

推导： $\left \| \mathbf{X} \mathbf{u} \right \|_2^2 = \mathbf{u}^{\top} \mathbf{X}^{\top} \mathbf{X} \mathbf{u} \leq \lambda_{\max}(\mathbf{X}^{\top} \mathbf{X}) \mathbf{u}^{\top}\mathbf{u}=\lambda_{\max}(\mathbf{X}^{\top} \mathbf{X})$ ，等号成立当且仅当 $\mathbf{u}$ 为 $\lambda_{\max}$ 对应的特征向量

当a=b=∞时，

最大行和(max-row-sum)范数： $\left \| \mathbf{X} \right \|_{\infty}=\max_{i=1,\cdots,m}\sum_{j=1}^{n}\left | \mathbf{X}_{ij} \right |$

推导：考虑X的第i行，若 $\mathbf{X}_{ij}$ 为负数，则取 $\mathbf{u}_j$ 为-1，否则取 $\mathbf{u}_j$ 为1，易得此时取得最大值

对偶范数（A.1.6）

定义：在范数 $\left \| \cdot \right \|$ 的意义下，元素 $\mathbf{z}$ 的对偶范数为

$\left \| \mathbf{z} \right \|_* = \sup \{ <\mathbf{z}, \mathbf{x}> | \left \| \mathbf{x} \right \| \leq 1 \}$

向量的对偶范数

从定义出发，我们可以得到不等式 $\mathbf{z}^{\top} \mathbf{x} = \left \| \mathbf{x} \right \| \left ( \mathbf{z}^{\top} \frac{\mathbf{x}}{\left \| \mathbf{x} \right \|} \right ) \leq \left \| \mathbf{x} \right \| \left \| \mathbf{z} \right \|_*$

根据Hölder's inequality，易得结论：当 $\frac{1}{p}+\frac{1}{q}=1$ 时，范数和范数互为对偶范数

范数和 $l_\infty$ 范数互为对偶范数，范数的对偶范数是其本身

矩阵的对偶范数

考虑矩阵 $\mathbf{X}$ 在范数下的对偶范数，有 $\left \| \mathbf{Z} \right \|_{2*} = \sup \{ \textbf{tr} (\mathbf{Z}^{\top} \mathbf{X}) | \left \| \mathbf{X} \right \|_2 \leq 1\} =\sigma_1(\mathbf{Z}) + \cdots +\sigma_r(\mathbf{Z}) =\textbf{tr} (\mathbf{Z}^{\top} \mathbf{Z})^{1/2}$

这一步的证明还没有搞懂，暂时先略过

1.3 范数的性质（A.1.2/A.1.4）、距离、单位球

范数的四个性质： ①非负性 ②正定性 ③齐次性 ④满足三角不等式

范数的等价性（A.1.4）：还未见其应用，故先略过

距离：两个元素差的范数 $\textbf{dist}(\mathbf{x}, \mathbf{y}) = \left \| \mathbf{x} - \mathbf{y} \right \|$

单位球：到原点距离不超过1的元素组成的集合

①关于原点对称 ②凸集 ③闭集、有界、有非空内点

2.分析

2.1 开集、闭集

数学分析课上讲过的两个概念，如果一个集合中的点均为其内点，则该集合为开集。如果一个集合的补集是开集，则称该集合为闭集。

2.2 上确界、下确界

上下确界可以理解为无限集上的最大值和最小值，根据确界存在定理，一个集合的上下确界必定存在。定义不再赘述。

3. 函数

3.1 函数记号

函数 $f : \textbf{A} \rightarrow \textbf{B}$ ,表示集合A到集合B的一个映射，其中函数f的定义域 $\textbf{dom} f \subseteq \textbf{A}$ 。这里集合A和集合B通常是向量、矩阵组成的集合。

3.2 连续性

函数的连续性也是数学分析的基础内容，不多做赘述。

3.3 闭函数

函数 $f:\mathbb{R}^{n} \rightarrow \mathbb{R}$ 是闭的，当且仅当对于任意的 $\alpha \in \mathbb{R}$ ，它的sublevel set $\{\mathbf{x} \in \textbf{dom} f | f(\mathbf{x})\leq \alpha \}$ 是闭集。

该定义等价于函数f的epigraph $\textbf{epi} f = \{ (\mathbf{x}, t) \in \mathbb{R}^{n+1} | \mathbf{x} \in \textbf{dom} f, f(\mathbf{x})\leq t\}$ 是闭集。

若已知函数f的连续性，当符合下列情况时，函数f是闭函数：

①f的定义域是闭集

②f的定义域是开集，但函数f在定义域的边界点处，函数值趋于∞

函数 $f(x)=x log x, \textbf{dom} f = \mathbb{R}_{++}$ 不是闭函数，因为0是其定义域的边界点，而当x-->0时，f(x)-->0

4. 导数

4.1 导数与梯度

函数 $f:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ 的在x点的导数记作矩阵 $Df(x) \in \mathbb{R}^{m \times n}$ ,满足

$\lim_{\mathbf{z} \in \textbf{dom}f, \mathbf{z} \neq \mathbf{x},\mathbf{z} \rightarrow \mathbf{x}} \frac{\left \| f(\mathbf{z}) - f(\mathbf{x}) - Df(\mathbf{x})(\mathbf{z}-\mathbf{x}) \right \|_2}{\left \| \mathbf{z} - \mathbf{x} \right \|_2} = 0$

其中， $Df(\mathbf{x})_{ij} = \frac{\partial f_i(\mathbf{x})}{\partial \mathbf{x}_j} (i = 1, \cdots, m, j=1, \cdots, n)$

函数在x点附近的一阶近似(first-order approximation)为 $f(\mathbf{x}) + Df(\mathbf{x})(\mathbf{z} - \mathbf{x})$

梯度

函数 $f:\mathbb{R}^n \rightarrow \mathbb{R}$ 的导数 $Df(\mathbf{x}) \in \mathbb{R}^{1 \times n}$ ，是行向量，定义其梯度为 $\nabla f(\mathbf{x}) = Df(\mathbf{x})^{\top}$

故其中， $\nabla f(\mathbf{x})_i = \frac{\partial{f(\mathbf{x})} }{\partial\mathbf{x}_i} i=1,\cdots,n$

例1：

二次函数 $f:\mathbb{R}^n \rightarrow \mathbb{R}$ , $f(\mathbf{x}) = (1/2) \mathbf{x}^{\top} \mathbf{P} \mathbf{x} + \mathbf{q}^{\top} \mathbf{x} + r$ ，其中 $\mathbf{P} \in \mathbb{S}^{n}, \mathbf{q} \in \mathbb{R}^n, r \in \mathbb{R}$

其在x处的梯度为 $\nabla f (\mathbf{x}) = \mathbf{P} \mathbf{x} + \mathbf{q}$

例2：

对数函数 $f : \mathbb{S}^n_{++} \rightarrow \mathbb{R}$ , $f(\mathbf{X}) = \log \ \det \mathbf{X}$

微分法，记 $\mathbf{Z} \in \mathbb{S}^{n}_{++} , \Delta \mathbf{X} = \mathbf{Z} - \mathbf{X}$ ，则

$\log \ \det \mathbf{Z} &= \log \ \det(\mathbf{X} + \Delta \mathbf{X}) \\ &= \log \ \det \left( \mathbf{X}^{1/2} (\mathbf{I} + \mathbf{X}^{-1/2} \Delta \mathbf{X} \mathbf{X}^{-1/2})\mathbf{X}^{1/2} \right) \\ &= \log \ \det \mathbf{X} + \log \det (\mathbf{I} + \mathbf{X}^{-1/2} \Delta \mathbf{X} \mathbf{X}^{-1/2}) \\ &= \log \ \det \mathbf{X} + \sum_{i=1}^{n} \log (1+ \lambda_i)$

其中， $\lambda_i$ 是矩阵 $\mathbf{X}^{-1/2} \Delta \mathbf{X} \mathbf{X}^{-1/2}$ 的第i个特征值。因为 $\Delta \mathbf{X}$ 趋近于0，所以 $\lambda_i$ 趋近于0， $\log (1+\lambda_i) \approx \lambda_i$

$\log \ \det \mathbf{Z} \approx \log \det \mathbf{X} + \sum_{i=1}^n \lambda_i \\ = \log \det \mathbf{X} + \textbf{tr}(\mathbf{X}^{-1/2}\Delta \mathbf{X} \mathbf{X}^{-1/2})\\ = \log \det \mathbf{X} + \textbf{tr}(\mathbf{X}^{-1}\Delta \mathbf{X} ) \\ = \log \det \mathbf{X} + \textbf{tr}\left(\mathbf{X}^{-1} (\mathbf{Z} - \mathbf{X}) \right)$

对照一阶近似公式， $f(\mathbf{Z}) = f(\mathbf{X}) + \left< D f(\mathbf{X}), \mathbf{Z} - \mathbf{X} \right>$

可得， $Df(\mathbf{X}) = \mathbf{X}^{-1}$ ，与公式 $D (\log x) = \frac{1}{x}$ 吻合

4.2 链式法则

函数 $f:\mathbb{R}^n \rightarrow \mathbb{R}^m$ 和函数 $g:\mathbb{R}^m\rightarrow \mathbb{R}^p$ 均可维，则其复合函数 $h:\mathbb{R}^n \rightarrow \mathbb{R}^p$ ， $h(\mathbf{x})=g(f(\mathbf{x}))$ 可微，其在点x处的导数为

$Dh(\mathbf{x}) = Dg(f(\mathbf{x})) Df(\mathbf{x})$

线性复合：函数 $g(\mathbf{x}) =f( \mathbf{A} \mathbf{x} + \mathbf{b}), \mathbf{A} \in \mathbb{R}^{n \times p}, \mathbf{b} \in \mathbb{R}^n$ ，则函数g的梯度为

$\nabla g(\mathbf{x}) = \mathbf{A}^{\top} \nabla f(\mathbf{A}\mathbf{x} + \mathbf{b})$

例1：

求导： $f(\mathbf{x}) = \log \sum_{i=1}^m \exp(\mathbf{a}_i^{\top}\mathbf{x} + \mathbf{b}_i) \ \ \ \mathbf{a}_i \in \mathbb{R}^n, \mathbf{b}_i \in \mathbb{R}$

定义 $g(\mathbf{x}) = \log \sum_{i=1}^m \exp \mathbf{x}_i \ \ \ h(\mathbf{x}) = \mathbf{A}\mathbf{x} + \mathbf{b}$ ，则 $f(\mathbf{x})=g(h(\mathbf{x}))$

$\nabla g(\mathbf{A} \mathbf{x} +\mathbf{b}) = \frac{1}{\mathbf{1}^{\top} \mathbf{z}} \mathbf{z}, \ \ \ \mathbf{z}_i = \mathbf{a}_i^{\top} \mathbf{x} + \mathbf{b}_i$

$\nabla f(\mathbf{x}) = \mathbf{A}^{\top} \nabla g(h(\mathbf{x})) = \frac{1}{\mathbf{1}^{\top} \mathbf{z}} \mathbf{A}^{\top} \mathbf{z}$

例2：

求导： $f(\mathbf{x}) = \log \det (\mathbf{F}_0 + \mathbf{x}_1 \mathbf{F}_1 + \cdots + \mathbf{x}_n \mathbf{F}_n), \ \ \ \ \mathbf{F}_i \in \mathbb{S}^p$ 且 $\mathbf{F}_0 + \mathbf{x}_1 \mathbf{F}_1 + \cdots + \mathbf{x}_n \mathbf{F}_n \succ \mathbf{O}$

$\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}_i} = \textbf{tr} (\mathbf{F}_i \nabla \log \det \mathbf{F}) = \textbf{tr}(\mathbf{F}^{-1} \mathbf{F}_i)$ ，其中 $\mathbf{F} = \mathbf{F}_0 + \mathbf{F}_1 \mathbf{x}_1 + \cdots + \mathbf{F}_n \mathbf{x}_n$

4.3 二阶导数

函数 $f:\mathbb{R}^n \rightarrow \mathbb{R}$ 的二阶导数(Hessian matrix)记为 $\nabla^2 f(\mathbf{x})$ ，其中 $\nabla^2 f(\mathbf{x})_{ij} = \frac{\partial^2 f(\mathbf{x})}{\partial \mathbf{x}_i \partial \mathbf{x}_j}, \ \ \ i=1, \cdots , n , j =1, \cdots, n$

函数f在点x处的二阶近似为 $\widehat{f}(\mathbf{z}) = f(\mathbf{x}) + \nabla f(\mathbf{x})^{\top} (\mathbf{z} - \mathbf{x}) + (1/2) (\mathbf{z} - \mathbf{x})^{\top} \nabla^2 f(\mathbf{x}) (\mathbf{z} - \mathbf{x})$

例1：

求导：二次函数 $f(\mathbf{x}) = (1/2) \mathbf{x}^{\top} \mathbf{P} \mathbf{x} + \mathbf{q}^{\top} \mathbf{x} + r$ ，其中 $\mathbf{P} \in \mathbb{S}^n, \mathbf{q} \in \mathbb{R}^n, r \in \mathbb{R}$

$\nabla^2 f(\mathbf{x}) = \mathbf{P}$

例2：

求导：对数函数 $f(\mathbf{X}) = \log \det \mathbf{X}$ ，其中 $\mathbf{X} \in \mathbb{S}^n_{++}$

记 $\Delta \mathbf{X} = \mathbf{Z} - \mathbf{X}$ ，

$\nabla f(\mathbf{X}) = \mathbf{X}^{-1}$

因为当A很小时，有 $(\mathbf{I} + \mathbf{A})^{-1} \approx \mathbf{I} - \mathbf{A}$

$\mathbf{Z}^{-1} = (\mathbf{X} + \Delta \mathbf{X})^{-1} \\ = \left( \mathbf{X}^{1/2} (\mathbf{I} + \mathbf{X}^{1/2} \Delta \mathbf{X} \mathbf{X}^{1/2})\mathbf{X}^{1/2} \right )^{-1} \\ \approx \mathbf{X}^{-1/2} (\mathbf{I} - \mathbf{X}^{-1/2} \Delta \mathbf{X} \mathbf{X}^{-1/2})\mathbf{X}^{-1/2} \\ =\mathbf{X}^{-1} - \mathbf{X}^{-1} \Delta \mathbf{X} \mathbf{X}^{-1}$

$f(\mathbf{Z}) = f(\mathbf{X}+\Delta \mathbf{X}) \\ \approx f(\mathbf{X}) + \textbf{tr} (\mathbf{X}^{-1} \Delta \mathbf{X}) - (1/2) \textbf{tr}(\mathbf{X}^{-1} \Delta \mathbf{X} \mathbf{X}^{-1} \Delta \mathbf{X}) \\ \approx f(\mathbf{X}) + \textbf{tr}(\mathbf{X}^{-1} (\mathbf{Z}-\mathbf{X})) - (1/2) \textbf{tr}(\mathbf{X}^{-1}(\mathbf{Z}-\mathbf{X})\mathbf{X}^{-1}(\mathbf{Z} - \mathbf{X}))$

这里要注意，向量的二次形式可以写作二次型 $\mathbf{x}^{\top} \mathbf{A} \mathbf{x}$ ，而矩阵的二次形式可写作 $\textbf{tr}(\mathbf{A}^{-1} \mathbf{U} \mathbf{A}^{-1} \mathbf{V})$

4.4 二阶导数的链式法则

单值函数的复合：函数 $f: \mathbb{R}^n \rightarrow \mathbb{R}, g:\mathbb{R} \rightarrow \mathbb{R}$ ，令函数 $h(\mathbf{x}) = g(f(\mathbf{x}))$ ，则h的二阶导数

$\nabla^2 h(\mathbf{x}) = g'(f(\mathbf{x})) \nabla^2 f(\mathbf{x}) + g''(f(x)) \nabla f(\mathbf{x}) \nabla f(\mathbf{x})^{\top}$

线性函数的复合：函数 $f:\mathbb{R}^n \rightarrow \mathbb{R}, g:\mathbb{R}^m \rightarrow \mathbb{R}$ ，令函数 $g(\mathbf{x}) = f(\mathbf{A} \mathbf{x} + \mathbf{b})$ ，其中 $\mathbf{A} \in \mathbb{R}^{n \times m}, \mathbf{b} \in \mathbb{R}^n$ ，则g的二阶导数

$\nabla^2 g(\mathbf{x}) = \mathbf{A}^{\top} \nabla^2 f(\mathbf{A} \mathbf{x} +\mathbf{b}) \mathbf{A}$

以上两个公式可与单值函数的链式法则进行对比得出。

例：