论文阅读笔记集合（持续更新）

深度学习检测算法选择

两种最常用算法比较：

RetinaNet             简单、精度略低、速度快、fp较多
FPN + Faster R-CNN    较复杂、精度高、fp少、速度较慢

上面两种为one stage算法和two stage算法最常用的baseline。yolo和SSD算法因为检测精度较低，虽然速度快但是应用较少。
base model的演化：
base model一开始用Alexnet，后来则是VGG和GoogleNet。ResNet出来后，基本采用ResNet作为base model，以及ResNet的各种变体。
算法开发流程：
一般使用ResNet50或ResNet50 half（channel减半）backbone，使用pretrain model，再fine_tune验证有效性。之后如果追求速度（算法落地），那么将basemodel替换为Xception-145、ShuffleNet、MobileNet、Efficientnet等；如果追求精度（如发论文、打比赛），则将backbone替换为ResNet-101、ResNet-152、DenseNet等。如果要蒸馏，可以用ResNet-101、ResNet-152 backbone先训练精度较高的模型，再蒸馏小的backbone，如ResNet50。
当使用当前backbone点数较低时，可以先用大一号的backbone训一次，观察点数差距是否为两个backbone正常的点数差距，如果是，说明当前backbone从样本中提取特征的能力有限，考虑加入一些更容易学习的样本或者使用大一号backbone蒸馏当前模型；如果不是，可能样本量偏少了，需要增加和当前样本同等质量的数据。
如果是为了做实验，验证结果，可以采用一个小一些的backbone，以一天内能够训练+测试完为限，如ResNet50 half这样的小模型；先解决性能瓶颈，如加载数据时间过长等等；做实验时先去掉其他trick，以backbone+基本loss来进行实验。

review or survey of one field paper

Deep Learning for Fine-Grained Image Analysis: A Survey

文章地址：https://arxiv.org/pdf/1907.03069v1.pdf
详细介绍了细粒度分类的定义，细粒度分类的常见数据集，细粒度分类常见模型方法的种类，还介绍了细粒度检索的问题。

Imbalance Problems in Object Detection: A Review

文章地址：https://arxiv.org/pdf/1909.00169.pdf
关于目标检测不平衡问题的综述文章，文中介绍了四种不平衡类型：类别不平衡，尺度不平衡，目标不平衡和边界框不平衡。
前景和背景类存在类别不平衡，不同前景类之间也存在类别不平衡；某类物体的不同尺度的样本数量不同时，发生尺度不平衡，或者特征尺度也可能不平衡；空间不平衡是回归loss不平衡，Iou分布的不平衡，以及对象位置的不平衡；当存在多个损失函数以最小化时发生目标不平衡，比如分类和回归损失的不平衡。
本文对上面四种不平衡问题进行了总结，并列出了今年来对这些问题进行改进的论文和改进思路。

Recent Advances in Deep Learning for Object Detection

文章地址：https://arxiv.org/pdf/1908.03673.pdf
介绍了几种常见的backbone如VGG16，ResNet，DenseNet，ResNeXt，GoogleNet，Hourglass。目标检测网络模型的发展过程中著名的目标检测网络模型，学习策略，应用方向和著名benchmark。

A Survey of Deep Learning-based Object Detection

文章地址：https://arxiv.org/pdf/1907.09408.pdf
介绍R-CNN、Fast R-CNN、Faster R-CNN、Mask R-CNN、YOLO、YOLOv2、YOLOv3、RetinaNet、SSD、DSSD、RefineDet、Relation Networks for Object Detection、DCNv2、NAS-FPN、M2Det等目标检测网络，介绍了PASCAL VOC dataset、MS COCO benchmark、 ImageNet benchmark等数据集，同时还介绍了一些对基于物体检测的四个步骤（图像预处理，特征提取，分类和回归，后处理）中某个步骤进行改进的文章。

Understanding Deep Learning Techniques for Image Segmentation

文章地址：https://arxiv.org/pdf/1907.06119.pdf
介绍了从2013年到2019年，主流的30多种分割算法（含语义/实例分割），50多种数据集。

Deep Learning in Video Multi-Object Tracking: A Survey

文章地址：https://arxiv.org/pdf/1907.12740.pdf
介绍视频多目标跟踪技术今年来的发展，介绍了多目标跟踪模型、度量函数、数据集。

Deep Face Recognition: A Survey

文章地址：https://arxiv.org/pdf/1804.06655.pdf
介绍了人脸识别的分类，人脸检测的流程，不同的网络结构和损失函数，人脸处理的一些算法，人脸数据集等等。

The Six Fronts of the Generative Adversarial Networks

文章地址：https://arxiv.org/pdf/1910.13076.pdf
一篇有关GAN的综述文章，总结了2014年至今GAN网络的论文，主要从网络结构、条件信息、归一化和约束、损失函数、图像转换、评估准则六个方面做了简洁的梳理和回顾。

A Methodological Review of Visual Road Recognition Procedures for Autonomous Driving Applications

文章地址：https://arxiv.org/pdf/1905.01635.pdf
总结了近年来的道路识别和检测算法。

image classification

image classification backbone model

Deep Residual Learning for Image Recognition

文章地址：https://arxiv.org/pdf/1512.03385.pdf
本文即大名鼎鼎的resnetv1网络。该网络是一个通用的特征提取网络，可用于分类、检测、分割等，是目前应用最为广泛的网络之一。
本文先提出更深的网络性能反而退化这一现象，然后提出了解决方法：残差模块。每个模块学习的是残差F（x）而不是整个H（x）。残差模块结构如下：

一般的深层网络拟合非线性函数H（x），即输入等于输出，残差网络将H（x）拆分为两部分：
$$H(x)=x+(H(x)-x)=x+F(x)$$
这样就变成了优化残差F（x）。此时深层网路=浅层网络+附加层，附加层输入x，去拟合残差F（x）比拟合H（x）更加容易。另外，如果浅层网络已经拟合的比较好，附加层学到的残差数量级也会很小，这样网络就对较小数量级的变化更加敏感。
通过在残差模块的最后输出上加上前两层的输入，使得中间两层学习的是输入与输出之间的残差F（x）。在实际创建更深的网络的时候，为了减轻训练负担，ResNet采用间隔1x1卷积、3x3卷积、1x1的三层网络，第一层用于降低维度，第三层用于升高维度。这种结构称为Bottleneck，并将bottleneck的输入加在最后1x1卷积的输出上。使用快捷连接（Shortcut Connections）将输入加到输出时要保证输入和输出具有相同的维度。如果输入和输出尺寸相同，可以直接使用快捷连接。如果不同，则有两种方式使得输入和输出相同：第一种是额外填充零值的行，增加维度；第二种是用1x1卷积核，步长为2。
resnetv1各网络结构：

其中18和34的基本结构叫basic block，50、101、152的基本结构叫bottleneck block。即下图所示：

Identity Mappings in Deep Residual Networks

文章地址：https://arxiv.org/pdf/1603.05027.pdf
这篇文章即resnetv2网络。本文的改进在于，当前向参数和反向梯度直接从block传到下一个block，而不必经过relu操作时效果更好。原始的残差模块和改进的残差模块对比如下：

可以看到改进后的残差模块（proposed）将relu全部移动到了主分支上，在快捷连接上不使用relu。
首先给出残差网络的公式：
$$\begin{array}{rl}{\mathbf{y}}_l=& h\left({\mathbf{x}}_l\right)+F\left({\mathbf{x}}_l,W_l\right)\\ & {\mathbf{x}}_{l+1}=f\left({\mathbf{y}}_l\right)\end{array}$$
在resnetv1中：
$$h\left({\mathbf{x}}_l\right)={\mathbf{x}}_l$$
上式即恒等映射。f是relu激活函数。
ResNet V2的思想是现在让这种恒等映射不仅仅发生在单个的残差模块中，而是贯穿在整个网络之中。即同时满足：
$$\begin{gathered} h\left({\mathbf{x}}_l\right)={\mathbf{x}}_l \\ f\left({\mathbf{y}}_l\right)={\mathbf{y}}_l \end{gathered}$$
然后分析了五种不同的快捷连接情况（b-f），并做了实验：

b即constant scaling，分为两种情况，第一种情况只有shortcut有scale，第二种情况与highway gating相同。前一种情况很容易导致梯度爆炸或梯度衰减，不能收敛，第二种错误率比ResNet V1要高；c即exclusive gating，借鉴自Highway Networks的门控机制，我们发现偏置项bg的初始化对于门控模型的训练至关重要，当bg的初始化不合理时，exclusive gating网络并不能收敛到一个好的结果；d即shortcut-only gating是exclusive gating的简化，这种情况下，函数F不进行缩放；只有捷径连接由1−g（x）进行缩放，偏置项bg的初始值同样很重要；e即convolutional shortcut，在shortcut上先经过一个1x1的卷积，当叠加了很多个残差模块时，即使每个残差模块上只有1个1x1卷积模块，也会对信息传播造成阻碍，所以110层的ResNet的结果很差，训练误差也变得很高；f即Dropout shortcut，在shortcut上做dropout，Dropout在统计学上相当于给捷径连接强加了一个λ的缩放，这和constant scaling很类似，同样的阻碍了信号的传播。
下面研究了激活函数relu的位置安排在哪里使得f成为一个恒等映射。同样设置了几组实验：

b是add后再bn+relu，这样的结果比基本结构的结果要差很多，原因是阻碍了信息在不同残差模块之间的恒等映射上的传递；c是先bn+relu后再add，这使得本层残差块拟合的残差只有大于0的值，但实际上残差有可能为正也有可能为负，使得拟合更加不准，结果也更差。
接下来作者证明了如果一个新的附加激活f是非对称的，则后激活和下一个层的预激活是等价的。作者设计了只使用relu的预激活（d），和使用了bn+relu的全预激活（e）。 实验发现只使用relu预激活的结果与ResNetv1-110/164的很接近。这个relu层不与bn层连接使用，因此无法共享bn所带来的好处。当bn和relu都用在预激活上，结果得到了很可观的提高。
由于输入x在两个残差模块之间能够很直接的进行传递。因此resnetv2-1001网络的训练误差能够降低的特别快。如果ResNet层数不多时（如164层），f=relu（x）的影响并不是很强烈。在训练初期，训练曲线似乎收到了一点影响，但是马上回归到良好的状态。通过监控模型的响应，我们观测到，这是因为在经过一定的训练后，权重被调整到使得yl总是大于0的，因此f并不会截断它（由于先前relu的存在，xl 总是非负的，因此只有当F是很大的负数时，yl才会小于0）。当时在使用1000层的模型时，这种截断就会更加频繁。

Wide Residual Networks

文章地址：https://arxiv.org/pdf/1605.07146v1.pdf
本文作者认为，带有恒等映射的残差模块允许训练非常深的网络，但同时这也是残差网络的弱点。当梯度流过网络时，没有什么可以强迫它通过残差块权重，这样残差块就有可能在训练中学不到东西，因此最终有可能只有少数几个残差块学习到了有用的表示，而绝大多数的残差块起到的作用并不大。
作者认为，与增加残差网络的深度相比，ResNet残差块在channel上的扩展提供了一种提高残差网络性能的更为有效的方法。例如，作者wrn16-8与resnet1001具有基本相同的精度和参数量，但是训练速度却要快几倍。本文实验的实验表明， 适当的增加ResNet中残差模块的宽度（channel）比增加网络深度可以更有效的提升性能 ，这说明残差网络的能力主要由残差模块提供，网络深度只有补充性的作用。 由于加宽的残差模块中包含大量参数，我们需要使用dropout来防止过拟合。ResNetv2网络中将dropout加到快捷连接支路上发现性能变差，因此本文作者将dropout添加到残差支路中，实验证明该方法可以提升网络性能。
在ResNet-v2中残差网络有两种形式的block：basic block，即两个相连的3x3卷积层，预激活（pre-activation）形式，下图a所示；bottleneck block，即一个3x3卷积层加上前后各一个1x1卷积层，下图b所示。bottleneck block是为了在增加层数时减少block的计算量，也就是使得block更窄，而我们要考察的是加宽block的效果，所以不考虑bottleneck block，在本文架构中只使用basic block形式。

提升残差模块的表示能力有三种方法：

• 向每个block中增加更多的卷积层；
• 通过增加特征图数量来加宽卷积层，即增加channel数；
• 增大卷积层的卷积核尺寸。

在VGG、Inception-v4网络中表明，小尺寸的卷积核更有效，因此本文不考虑大于3x3的卷积核。
首先作者对方法1尝试了下列几种组合：

3表示3x3卷积，1表示1x1卷积。为了保持总层数不变，当深度因子l（表示一个block中包含的卷积层数量）变化时，残差块总数d也要变化，如增大l时应该减小d。宽度因子k表示卷积层输出特征图数量的倍数，即channel的倍数。
当深度因子l或者残差块总数d增大时，模型参数量也线性增加；而宽度因子k增大时，参数量和计算复杂度会增加k的平方倍。即使时这样，计算加宽的网络也比窄但极深的网络更加高效，因为GPU在并行计算大的张量时更加高效。在ResNet之前的网络架构都是比较宽的，比如Inception和VGG。本文以WRN-n-k表示包含n个卷积层且宽度因子为k的WRN，也有可能加上block的形式，比如WRN-40-2-B（3,3）。
加宽残差块会增加网络的参数量，所以要使用正则化方法。之前的残差网络使用BN来提供正则化的效果，但仍然需要大量的数据增广操作。本文在残差函数支路中加入dropout来避免过拟合（即上图d）。在极深层残差网络中这样应该可以解决特征重复利用逐渐减少的问题，因为dropout的加入可以强使不同的残差block学习表示。
方法1的几种方案，只要总参数量差不多，则性能也差不多。最后着重选了3x3卷积来做实验，控制深度因子l发现，B（3,3）比B（3,3,3,3）、B（3,3,3）、B（3）要好，前两者可能是因为优化困难。

再考察不同的宽度因子k和网络深度的组合，网络性能如下：


最后发现，WRN40-4与ResNet1001结果相似，参数数量相似，但是前者训练快8倍。
实验结果总结：

• 加宽不同深度的残差网络都可以提升性能；
• 在参数量过多和需要更强的正则化方法之前，增加深度和宽度都有助于提升性能；
• 相同参数时，更宽的网络比更深的网络好训练。此外，更宽网络可以训练出数倍于窄网络参数量的模型，而窄网络的深度需要加倍才能得到相同的结果，这使得训练几乎不可行；
• dropout可以和加宽方法互补使用来进一步提升模型性能。

Aggregated Residual Transformations for Deep Neural Networks

文章地址：https://arxiv.org/pdf/1611.05431.pdf
本文即ResNeXt网络。传统模型要提高模型的准确率的改进方式都是通过加深或加宽网络，但是这样计算开销也会增加的很快。而ResNeXt网络可以在不增加参数量和计算开销的情况下提高模型准确率。作者同时采用VGG的堆叠思想和Inception的 split-transform-merge的思想，提出在cardinality上进行改进，原文解释为"the size of the set of transformations"，实际上就是对某一层在channel上进行分组卷积，cardinality就是分组数。作者做的一系列实验表明增加cardinality比增加深度和宽度更有效，且不增加参数量和计算开销。
ResNeXt残差模块形式：

上图是ResNet和ResNeXt残差模块的对比，可以看到就是将原来的64channel变成现在的32组4channel卷积。
ResNeXt残差模块有三种等价形式：

a就是前面所说的aggregated residual transformations，即前面图中的右图；b则采用两层卷积后concatenate，再卷积，有点类似Inception-ResNet，只不过这里的每条path都是相同的拓扑结构（卷积核大小相同）；c采用了分组卷积。作者在文中明确说明这三种结构是严格等价的，并且这三种结构的结果一模一样，但由于分组卷积的速度更快，因此后面采用了分组卷积的形式。
分组卷积最早在alexnet中使用，当时是为了解决一个GPU中不能处理一个很大channel数的feature map，所以将feature map按channel分了几组，分别在不同的GPU中卷积，最后再把结果融合。但事实上，即使是在同一个GPU中做分组卷积，也可以有效减少参数量。如：
input_channel=128，output_channel=128，kernel size=3x3时，普通卷积参数量为3x3x128x128；使用分组卷积时，若group num=32，则每个group的input_channel=4，output_channel=4，每个group参数量为3x3x4x4，总参数量为3x3x4x4x32，参数量只有原来的1/32。
论文中的实验结果表明，在同样的深度和复杂度下，ResNeXt正确率更高，且ResNeXt-101的性能就超过了ResNet-200。

Densely Connected Convolutional Networks

文章地址：https://arxiv.org/pdf/1608.06993.pdf
本文即DenseNet网络。
介绍这篇文章先先要介绍另一篇文章：Deep networks with stochastic depth（https://arxiv.org/pdf/1603.09382.pdf），这篇文章的作者和DenseNet网络作者是同一个人，文章的贡献主要是提出随机深度，在训练时随机在resnet网络中By pass一些层，而在测试时使用整个网络，这样在训练时时间较少且能够提高模型性能，思路和dropout很像，只是现在drop的是某些层。在网络训练过程中，随机去掉一些层并没有影响算法的收敛性，同时去掉中间几层对最终结果影响也很小，说明ResNet每一层学习的特征信息都非常少，也就是说，ResNet具有很好的冗余性。
作者使用残差块作为基本单位，在训练中，如果一个特定的残差块被启用了，那么它的输入就会同时流入shortcut和权重层，否则输入就只会流入shortcut。在训练的过程中，每一个层都有一个“生存概率”，并且都会被随机丢弃。在测试过程中，所有的block都将保持激活状态，而且block都将根据其在训练中的生存概率进行调整。这种方法减少了训练时间，并在四个数据集上（cifar-10, cifar-100, SVHN, imageNet）显著改善了测试错误率。
现在回到DenseNet网络。DenseNet网络论文开篇很直白地说：最近的研究表明，如果卷积网络在接近输入和接近输出的层之间包含较短的连接，那么，该网络可以显著地加深，变得更精确并且能够更有效地训练。本文基于这个观察提出了DenseNet网络。
DenseNet网络结构：

DenseNet网络中每两个层之间都有直接的连接，因此该网络的直接连接个数为Lx（L+1）/2。对于每一层，使用前面所有层的特征图作为输入，并且使用其自身输出的特征图作为所有后面层的输入。相比与ResNet，DenseNet的每个shortcut实现的是concate操作，而不是ResNet的add（summation）操作。
受到resnetv2网络的启发，现在将残差模块中的卷积变为BN->ReLU->Conv（3x3）的连续操作，称为复合函数。当concate时，前面浅层的feature map的hw可能是现在的feature map的两倍或更大，这时不能直接concate。因此，作者将网络划分为多个密集连接的密集块（见下图），将块之间的层称为过渡层，由过渡层进行卷积和池化。实验中使用的过渡层包括BN和1×1卷积，然后是2×2平均池化。

另外文章引入了一个增长率的概念。如果每个复合函数H输出k个feature map，那么第l层有k0+k×（l−1）个输入的feature map，其中k0是输入层的通道数，论文里面将k称为增长率（Growth rate）。DenseNet和resnet相比的一个优点是设置很小的k值，使得网络更窄从而参数更少。在dense block中每个卷积层的输出feature map的数量k都很小（小于100），而不是像其他网络一样动不动就几百上千的宽度。另外论文还观察到这种denseblock有正则化的效果，对过拟合有抑制作用。
对应于resnet的bottle neck block，Densenet也设计了bottle neck block，并将其称为DenseNet-B，即具有BN-ReLU-Conv（1×1）和BN-ReLU-Conv（3×3）版本的复合函数。这种bottle neck的设计对于DenseNet依然有效。
最后是不同的DenseNet的网络结构：

MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications

文章地址：https://arxiv.org/pdf/1704.04861.pdf
本文即MobileNetv1网络。这篇文章提出了一种可大幅度降低参数量的卷积方式：深度可分离卷积（Depthwise Separable Convolution）。可见下图：

这种卷积是将普通卷积进行了分解，分解成了一个depthwise convolution和一个1x1的卷积叫做pointwise convolution。depthwise卷积即对每个输入通道单独使用一个卷积核处理。pointwise卷积即对depthwise计算出来的结果进行1x1的卷积运算。标准的卷积运算是一步中就包含了filter计算和合并计算，然后直接将输入变成一个新的尺寸的输出。Depthwise separable convolution是将这个一步的操作分成了两层，一层做filter计算，一层做合并计算。这种分解的方式极大的减少了计算量和模型的大小。
举例：
假设输入channel=M，输出channel=N，feature map的h和w卷积前后保持不变，卷积核为3x3。即输入的feature map为（M，h，w），输出的feature map为（N，h，w）。
若使用标准卷积，则每个卷积核的尺寸为3x3xM，每个卷积核都在整个输入的feature map上卷积，输出的feature map为（1，h，w）。要输出channel=N，则要N个这样的卷积核，将每个卷积核输出的feature map在channel上concate起来，得到的feature map为（N，h，w）。
如果使用深度可分离卷积（Depthwise Separasble Convolution），这个标准卷积运算分成了两步：首先做Depthwise Convolution，每个 Depthwise Convolution的卷积核为3x3x1，共有M个卷积核，输出的feature map为（M，h，w）。然后做Pointwise Convolution， 每个 Pointwise Convolution卷积核为1x1xM，共有N个卷积核，得到的feature map为（N，h，w）。
这样参数量由3x3xMxN减少到3x3x1xM+1x1xMxN，可以看到减少了接近8/9的计算量。

作者还在文章提出了两个超参数来控制网络的大小：宽度因子（Width Multiplier）和分辨率因子（Resolution Multiplier）。宽度因子乘在input channel和output channel前，控制channel数。分辨率因子乘在feature map的宽高前，控制分辨率。

MobileNetV2: Inverted Residuals and Linear Bottlenecks

文章地址：https://arxiv.org/pdf/1801.04381.pdf
本文即MobileNetV2网络。本文的核心思想：线性瓶颈和倒置残差。
作者将经过激活层后的张量为感兴趣流形，维度为H×W×C，C为channel，文中称为宽度。作者说长期以来一直认为神经网络中感兴趣的流形可以嵌入到低维子空间中，即真实的感兴趣流形只是C个channel中的一个低维子空间。也就是说，我们降低C似乎就可以了。但是，由于我们的卷积后都会有ReLU激活函数，对于感兴趣流形占比大的低维子空间，通过relu层有较高的概率使得比较多的输出置0，这就会丢失许多有用的信息。如果经过relu后参数非0，那么输出和输入必定是经过了一个线性变换，也就是说此时relu仅仅是一个线性分类器。此外，作者认为如果输入流形可以嵌入到激活空间的一个子空间里（这个子空间可以通过Relu的非零部分），Relu可以保留信息并引入一定的复杂性。
由此得到结论：若经过ReLU后感兴趣流形都非零，就意味着其仅仅是经过了一个线性变换；若要保持输入的感兴趣流形的完整信息，就必须要让输入流形位于输入空间的低维子空间。
由此就可以给出解决方案，我们不能直接降低维度，因为channel数较低时通过relu层会有相对高的概率使较多的输出为0，要想不为0，就要使用relu的线性部分，相当于接了个线性分类器。因此使用linear bottleneck，消除了低维空间中relu对特征的破坏。要想保持输入的感兴趣流形的完整信息，那么就先升维再降维，即使用Inverted residuals block。
Linear Bottleneck：

即在MobileNetv1深度可分离卷积的基础上，添加了一个1×1的卷积层，使得feature map的值非零，消除低维空间中relu对特征的破坏。上图图c中是一个完整的Linear Bottleneck，深度卷积（ReLU6激活）->逐点卷积（ReLU6激活）->1×1卷积（Linear激活）。图d是图c紧跟着的下一层，即一个循环结构。
Inverted residuals block：

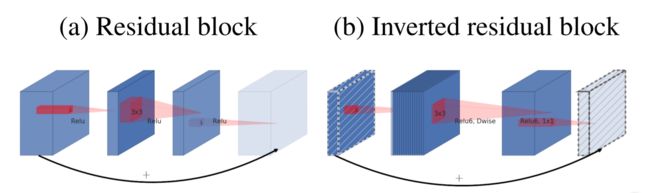
标准的残差模块是先降维后升维，但Bottleneck residual block是一个先升维后降维的一个流程，与标准残差刚好相反，所以叫做倒置残差。作者在linear bottleneck的第一层和第二层之间设置了一个扩展系数t（expansion factor），该系数用于增加整个linear bottleneck的通道数（即增加输入的维度，便于兴趣流形的恢复）。同时借用残差网络的思想，使用shortcut连接输入和输出。结合而成就成为Bottleneck residual block。
Bottleneck residual block具体结构：
逐点卷积（ReLU6激活）->深度卷积（ReLU6激活）->1×1卷积（Linear激活），然后shortcut连接。shortcut连接只在stride=1，输入输出维度相同的情况下才用到，其他情况都不会用到shortcut连接。

Searching for MobileNetV3

文章地址：https://arxiv.org/pdf/1905.02244.pdf
本文即MobileNetV3。MobileNetV3是用NAS搜索出来的。搜索基于NAS搜出来的MnasNet。使用了MobileNetV1的depthwise convolution和pointwise convolution，也使用了MobileNetV2的Inverted residuals block，同时还加入了SE模块（ squeeze and excitation）。使用了新的激活函数HardSwish，对嵌入式环境更友好。HardSwish公式如下：
$$\mathrm{h}-\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{h}[x]=x\frac{\mathrm{ReLU}6(x+3)}{6}$$
搜索出的结构有large和small两种：

ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices

文章地址：https://arxiv.org/pdf/1707.01083.pdf
本文即ShuffleNetv1网络。本文采用分组卷积（pointwise group convolution）与通道混合（channel shuffle）操作构造了一个新的轻量级网络。文中提出使用分组卷积去减少原本1x1卷积的计算复杂度，但是这样会打断chanel之间的信息流动，为此使用通道混合的机制来维持信息的流动性，对于其它的部分是使用深度可分离卷积实现计算量的降低。
ResNeXt网络中在3X3卷积层使用了分组卷积，但前后的1x1卷积仍然具有较大的计算量。为解决这个问题，可以在1x1卷积上也使用组卷积，这可以显著降低计算量。但是如果1x1组卷积和3x3组卷积相互叠加，可能会产生一种副作用：来自某个通道的输出仅来自一小部分的输入通道。这会弱化模型的表示能力。
如果我们允许组卷积从不同的组获得输入数据，输入和输出通道将完全相关。具体来说，对于从前一组卷积层生成的特征图，我们可以先将每个组中的通道划分为多个子组，然后在下一层中为每个组提供不同的子组。通过通道shuffle操作可以有效和优雅地实现这一点。假设一个由g个组构成一个卷积层，其输出有g×n个通道。我们首先将输出通道尺寸reshape为（g，n），转置然后将其展平为下一层的输入。即使两个卷积具有不同的组数，该操作仍然有效。此外，channel shuffle也是可微的，这意味着它可以嵌入网络结构中进行端到端的训练。

如上图，对a，输入的卷积被分为三个组，之后再在各个组上叠加卷积，存在的问题就是组间的信息是被阻隔的。由此提出b，将每个子组中的信息也进行划分，之后相互混合得到组合的信息；在此基础上使用更有效的方式实现得到c中的结构，这样shuffle操作之前和之后的group可以不同，且shuffle操作可微，能端到端进行训练。
由此提出ShuffleNet Unit：

a是使用深度可分离卷积加速之后的残差块，其1x1卷积部分的计算量还是比较大的。b是文章提出的Shuffle Unit，对1x1的卷积使用分组卷积进行替换，第一个分组卷积之后经过channel shuffle实现特征混合，再送入深度可分离卷积（注意这里没有使用ReLU）。c是b中stride为2时的网络结构。

ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design

文章地址：https://arxiv.org/pdf/1807.11164.pdf
本文即ShuffleNet V2网络。本文提出FLOPs不能作为衡量目标检测模型运行速度的标准，因为内存访问成本（Memory access cost）也是影响模型运行速度的一大因素。文中提出了四条准则：

• 输入通道数与输出通道数保持相等可以最小化内存访问成本（memory access cost,MAC）；
• 分组卷积中使用过多的分组数会增加内存访问成本（MAC）；
• 网络结构太复杂（分支和基本单元过多）会降低网络的并行程度；
• Element-wise 的操作消耗也不可忽略（包括ReLU，Tensor的相加，偏置相加等等操作）。

上图表示在4种网络都有相近的FLOPs，但是网络的速度在不同的平台上都不相同。因此，只通过FLOPs来衡量不是很准确。因为一些因素并没有考虑进去，一个就是内存访问成本（memory access cost,MAC），如当框架在执行分组卷积等操作时，运算能力强劲时可能可以忽略，但是在一些计算能力有限的平台上面就无法忽略了。还有就是网络的并行化程度，在相同的 FLOPs 下，网络并行化程度更高的网络速度更快。
作者根据上面的4条准则做了一系列实验，得到下列结论：

• 卷积层使用相同的输入输出通道数；
• 意识到使用大的分组数所带来的坏处；
• 降低网络结构的离散程度（减少分支以及所包含的基本单元）；
• 减少element-wise操作。

基于上面的结论，提出了ShuffleNet V2网络。

在shuffleNet中，depthwise convolution和瓶颈结构增加了MAC，用了太多的group，跨层连接中的element-wise Add 操作也比较多。所以在 shuffleNet V2 中增加了几种新特性：channel split即将通道数一分为2，化成两分支来代替原先的分组卷积结构（图c），并且每个分支中的卷积层都是保持输入输出通道数相同，其中一个分支不采取任何操作减少C，H，W，最后使用concate代替原来的elementy-wise add，并且后面不加ReLU，再加入channel shuffle来增加通道之间的信息交流。 对于下采样层，在这一层中对通道数进行翻倍。 在网络结构的最后，即平均值池化层前加入一层 1x1 的卷积层来进一步的混合特征。

EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

文章地址：https://arxiv.org/pdf/1905.11946.pdf
这篇文章先提出了一个观点，并用实验证明：单独放大channel，depth，resolution中的某一个因素，在acc达到80%左右后收益会迅速降低。因此，作者认为这三者之间存在一定的关系。比如，根据经验，对于更高分辨率的图像，应该增加网络深度，以便较大的接收场可以更好的提取特征，这些特征在较大的图像中包括更多的像素。相应地，当分辨率较高时，还应增加网络宽度。
因此，channel，depth，resolution应当满足某种关系一起放大，才能用最少的flops增加带来最大的acc提升。
作者提出来一种约束关系：
$$\begin{array}{rl}\text{ depth: }d& ={\alpha }^{\varphi }\\ \text{ width: }w& ={\beta }^{\varphi }\\ \text{ resolution: }& r={\gamma }^{\varphi }\\ \text{ s.t. }\alpha \cdot {\beta }^2\cdot {\gamma }^2& \approx 2\\ \alpha & \ge 1,\beta \ge 1,\gamma \ge 1\end{array}$$
这样改变φ时就是2的φ次方。首先作者将φ固定为1，网格搜索搜出最佳值α= 1.2，β= 1.1，γ= 1.15。这就是EfficientNet-B0。
然后将α，β，γ固定为常数，并使用不同φ值放大，得到EfficientNet-B1至B7。

        # Coefficients:   width,depth,res,dropout
        'efficientnet-b0': (1.0, 1.0, 224, 0.2),
        'efficientnet-b1': (1.0, 1.1, 240, 0.2),
        'efficientnet-b2': (1.1, 1.2, 260, 0.3),
        'efficientnet-b3': (1.2, 1.4, 300, 0.3),
        'efficientnet-b4': (1.4, 1.8, 380, 0.4),
        'efficientnet-b5': (1.6, 2.2, 456, 0.4),
        'efficientnet-b6': (1.8, 2.6, 528, 0.5),
        'efficientnet-b7': (2.0, 3.1, 600, 0.5),

EfficientNet系列相比resnet确实非常高效，如EfficientNet-B1 flops只有res152的1/16，但在imagenet上的top1 acc比res152还要高1.4个点。但要注意的是，flops降低到1/16的原因有很大一部分是因为采用了group conv（同样尺寸的卷积用group conv只有regular conv的1/9多一点），而group conv在gpu上的推理速度并不是regular conv的1/9，而是要慢的多。因此，efficientnet实际的推理速度取决于当前框架对group conv的计算效率。另外，论文中的训练方式非常另外，且包含的trick非常多，这个net在实际fine tune时的效果如何需要进一步验证（有人反馈在某些数据集上fine tune的效果不如resnet34）。

Res2Net: A New Multi-scale Backbone Architecture

文章地址：https://arxiv.org/pdf/1904.01169.pdf
本文模型可看下图：

本文对resnet的bottleneck进行了修改，将3×3卷积替换为分组逐次卷积再element wies add的操作，使得网络可以学习到multi-scale的feature。同时，修改后的Bottleneck还可以与ResNext和SENet中的基础block整合在一起。修改后的res2net50和原来的resnet50 flops和Inference time基本一致，模型性能有所提高。

receptive field

如何从前往后计算感受野

从前向后计算感受野的方法：
四个公式：
$$\begin{array}{rl}{n}_{out}& =\left|\frac{n_{in}+2p-k}{s}\right|+1\\ & \\ j_{out}& =j_{in}\ast s\\ & \\ r_{out}& =r_{in}+(k-1)\ast j_{in}\\ & \\ star{t}_{out}& =star{t}_{in}+\left(\frac{\mathrm{k}-1}{2}-\mathrm{p}\right)\ast j_{in}\end{array}$$
其中n为h和w的长度，r为当前层感受野的大小，j为两个相邻特征跳跃的距离，start为左上角特征（第一个特征）的中心坐标。注意feature map第一个特征的感受野的中心坐标就等于这个特征的中心坐标。
当卷积核大小为k，padding大小为p，步长为s时，第一个式子可计算出feature map的h和w长度；第二个式子计算输出feature map的特征间的间隔距离j，其等于上一层的间隔值乘以卷积的步长；第三个式子计算输出的feature map的感受野大小，其等于前一层感受野大小加上（k-1）xjin；第四个式子计算输出的feature map的第一个特征的感受野的中心坐标。
对于第一层输入层，n=image_size，r=1，j=1，start=0.5。

上面的计算方式还可以用递推公式计算：
$$l_k=l_{k-1}+\left(\left(f_k-1\right)\ast \prod _{i=1}^{k-1}{s}_i\right)$$
对于第一层输入层，l0=1，k=1，s=1。计算方式来自这里：http://shawnleezx.github.io/blog/2017/02/11/calculating-receptive-field-of-cnn/

还有一种更简单的推算方法：
初始feature map层的感受r=1。每经过一个kxk卷积核、s=1的卷积层感受野 r = r + (k - 1)。每经过一个kxk卷积核、s=2的卷积层或max/avg pooling层，感受野 r = (r x 2) + (k - 2)。1x1卷积核、s=1的卷积层不会改变感受野。对于FC层和GAP层，感受野就是整个输入的图像。对于多分支的网络，按照感受野最大的支路计算。shotcut、ReLU, BN，dropout等操作不影响感受野。整个网络全局的s等于所有层s的累乘。所有层的padding都可以等效加在输入图像，等效值P，直接用卷积的输入输出公式反推：
$$f_{out}=\left(f_{in}-r+2P\right)/S+1$$

Understanding the Effective Receptive Field in Deep Convolutional Neural Networks

文章地址：https://arxiv.org/pdf/1701.04128.pdf
本文提出了有效感受野的概念。上面的计算是理论感受野。理论感受野内的所有像素对输出的影响并不相同，事实上，理论感受野内的像素对输出的影响是按高斯分布的，如：

本文中将任何值大于中心点1-95.45％的像素都被视为有效感受野中的像素。本文的得出下列结论：

• 卷积核权重均匀分布和随机分布时，有效感受野服从（近似服从）Gaussian分布；
• ReLU操作的加入也会使得有效感受野服从（近似服从）Gaussian分布；
• dropout的加入不会改变有效感受野的Gaussian分布；
• 下采样和dilation会增加有效感受野的大小，其中下采样的效果更明显；
• skip-connections会减小有效感受野的大小；
• 只包含卷积层的情况下，随着卷积层数n的增加有效感受野按√n倍增加。同时，与理论感受野相比，有效感受野按1 /√n倍缩小。

network Visualization

Learning Deep Features for Discriminative Localization

文章地址：https://arxiv.org/pdf/1512.04150.pdf
本文即我们通常所说的CAM方法。在CAM中，要做可视化，需要将最后一层卷积层后先接一个GAP层，然后通过一个全连接层实现相应的分类结果，全连接层的权重称为w1，w2…。由于classification score是GAP之后的值与相应权重的乘积，因此可以看成是最后一层卷积的feature map与相应权重的乘积。即全连接层的每个权重代表最后一层卷积的feature map每个channel的feature map对最后的分类结果的贡献度，我们对其做element-wise muli后求和，就是CAM得到的Class Activation Map。
需要注意的是，在CAM之前已经有人用global max pooling来做类似的Activation Map，过程基本一样，就是GAP换成了global max pooling。但是GMP标注的结果更限于物体的某个关键点，而不能确定物体的完整轮廓。使用GAP会鼓励网络识别对象的完整范围。
CAM的缺点就是需要修改模型，添加GAP层和修改全连接层，并且需要重新训练，使用起来不太方便。

Grad-CAM: Why did you say that? Visual Explanations from Deep Networks via Gradient-based Localization

文章地址：https://arxiv.org/pdf/1610.02391.pdf
Grad-CAM全称是Gradient-weighted Class Activation Mapping，直接翻译是梯度加权分类激活映射。简单说就是用CNN做图像分类的时候，到底是根据图像的哪里来判断属于这个分类的，将模型关注的区域在图像上明确映射出来。
Grad-CAM是对CAM的推广，其基本思路和CAM是一致的，也是通过得到每个channel的feature map对应的权重，最后求一个加权和。它与CAM的主要区别在于求权重的过程。CAM通过替换全连接层为GAP层，重新训练得到权重，而Grad-CAM用梯度的全局平均来计算权重。计算对某个类C的第k个channel的feature map的权重：
$${\alpha }_k^c=\stackrel{\text{global average pooling }}{\frac{1}{Z}\sum _i\sum _j}\underset{\text{gradients via backprop }}{\frac{\partial y^c}{\partial A_{ij}^k}}$$
yc为进softmax前的类别c的分数，Ｚ为feature map像素点个数， Akij表示第k个channel的feature map中(i,j)位置处的值。
$$L_{\mathrm{G}\mathrm{r}\mathrm{a}\mathrm{d}-\mathrm{C}\mathrm{A}\mathrm{M}}^c=\mathrm{Re}LU(\underset{\text{linear contination }}{\sum _k{\alpha }_k^c{A}^k})$$
然后将feature map上每个点用每个channel的权重x值再求和，再经过relu函数。用relu函数是因为我们仅对当前的类具有正面影响的特征感兴趣，而负值特征可能属于图像中的其他类别，因此我们将其过滤掉。
Grad-CAM的最大好处就是不需要修改模型，也不需要重新训练模型，可以立即使用。

data augmentation

AutoAugment: Learning Augmentation Strategies from Data

文章地址：https://arxiv.org/pdf/1805.09501.pdf
本文通过NAS搜索得到了一种data augment的方式。搜索时以两个augment操作作为一个子策略，每个操作有两个超参需要搜索：应用操作的prob（0.1-1.0，十个离散值）和操作的level（0-10，11个离散值）。一共搜索了25组子策略，使用时生成一个随机index选择一个子策略，然后按顺序和操作的prob选择是否要使用这个子策略中的augment操作。
该搜索方法的搜索空间为（16×10×11）的10次方（25组子策略是分5次搜索的）。由于搜索空间太大，因此搜索时只用ImageNet的一个子集（120类，6000个sample）来进行搜索。

RandAugment: Practical automated data augmentation with a reduced search space

文章地址：https://arxiv.org/pdf/1909.13719.pdf
由于autoaugment的搜索空间太大，搜索时花的计算代价太大了。本文的搜索方法相当于一种简化。本文只设立了两个超参数：做几次augment操作和augment的level（所有augment操作固定为同一level），这样就将参数空间降低到了16x31（16个操作，31个level）。这样就大大缩短了搜索时间，同时现在可以在imagenet的整个数据集上进行搜索，这样可以避免在子集上搜索时容易搜索到次优解的问题。

GridMask Data Augmentation

文章地址：https://arxiv.org/pdf/2001.04086.pdf
本文方法效果图：

本文提出了一种替代autoaugment的data augment方法。该方法使用时用来替代autoaugment。即原本的augment策略是random crop+horizontal flip+autoaugment，使用本方法时为random crop+horizontal flip+grid mask。
本方法可以看成是生成一个随机的mask网格阵列。首先设定一个超参数r，r影响网格mask之间的间距。r与数据集的复杂程度密切相关，根据本文实验，imagenet上r=0.6效果最好，cifar10上r=0.4效果最好。确定r后，根据上式可计算出保留比率k。
$$k=1-(1-r{)}^2=2r-r^2$$
然后计算l：
$$l=r\ast d$$
其中d是一个完整单元的边长，取的是[96,224]间的随机数，一个完整单元内包含一个（1-r）xd大小的mask。
然后再根据下面的公式随机生成δx和δy，δx和δy决定了第一个完整单元距离图像左上角H和w的距离。
$${\delta }_x\left({\delta }_y\right)=\text{random}(0,d-1)$$
确定了r、d、δx和δy后我们就可以计算出一个阵列Mask，然后与原图相乘做augment。作者的开源代码中还发现生成mask后还会随机旋转（0，360）中某个角度。
本方法的亮点是只做一种data augmentation就超过了autoaugment的点数。虽然只有一种augment操作，但通过d，δx和δy这个变量的随机性保证了生成的增强图像的随机性。另外，作者认为一开始网络没有过拟合时不需要做augment，因此是逐渐增加augment的频率的。具体来说，即每张输入图像有0.8xmin（1,current_epoch/max_epoch）的概率做augment，否则不做augment。max_epoch是总epoch数×80%。
对于某些特殊任务，如reid任务，由于传统的颜色、亮度、对比度、旋转等augment操作都会掉点，只能使用random crop和random erase，本方法可以用来代替random erase。

trick

海康威视研究院ImageNet2016竞赛经验分享

文章地址：https://zhuanlan.zhihu.com/p/23249000
常用的data augmentation方法:

• Color Jittering：对颜色的数据增强：图像亮度、饱和度、对比度变化；
• PCA Jittering：首先按照RGB三个颜色通道计算均值和标准差，再在整个训练集上计算协方差矩阵，进行特征分解，得到特征向量和特征值，用来做PCA Jittering；
• Random Scale：尺度变换；
• Random Crop：采用随机图像差值方式，对图像进行裁剪、缩放；包括Scale Jittering方法（VGG及ResNet模型使用）或者尺度和长宽比增强变换；
• Horizontal/Vertical Flip：水平/垂直翻转；
• Shift：平移变换；
• Rotation/Reflection：旋转/仿射变换；
• Noise：高斯噪声、模糊处理；

这里有一篇文章介绍的很细致：https://www.zhihu.com/question/35339639/answer/406894510

本文使用的data augmentation方法:

• 对颜色的数据增强，包括色彩的饱和度、亮度和对比度等方面，主要从Facebook的代码里改过来的* PCA Jittering，最早是由Alex在他2012年赢得ImageNet竞赛的那篇NIPS中提出来的。我们首先按照RGB三个颜色通道计算了均值和标准差，对网络的输入数据进行规范化，随后我们在整个训练集上计算了协方差矩阵，进行特征分解，得到特征向量和特征值，用来做PCA Jittering。
• 在图像进行裁剪和缩放的时候，我们采用了随机的图像差值方式。
• Crop Sampling，就是怎么从原始图像中进行缩放裁剪获得网络的输入。比较常用的有2种方法：一是使用Scale Jittering，VGG和ResNet模型的训练都用了这种方法。二是尺度和长宽比增强变换，最早是Google提出来训练他们的Inception网络的。我们对其进行了改进，提出Supervised Data Augmentation方法。

Crop Sampling：
以往的Crop Sampling随机选取中心点，这样裁剪得到的图片可能不包含标签物体，改进后的方法如下：我先按照通常方法训练一个模型，然后用这个模型去生成真值标签的heatmap，这个Map指示了目标物体出现在不同位置的概率，再依据这个概率，在Map上随机选择一个位置，然后映射回原图，在原图那个位置附近去做Crop。通过引入这种有监督的信息，我们可以利用正确的信息来更好地训练模型，以提升识别准确率。
Label Shuffling：
一种在线式的类别平衡，即取出一个batch的数据后，对图像列表按照标签顺序进行排序（比如是三分类问题，标签为0，1，2，就按0，1，2的顺序排）。然后计算每个类别的样本数量，并得到样本最多的那个类别的样本数。根据这个最多样本数，对每类随机都产生一个随机排列的列表（比如标签2样本数最多为5，那么就对标签0，1，2各产生一个打乱的序号为0-4的列表）。然后用每个类别的列表中的数对各自类别的样本数求余，得到一个图片的索引。用这个索引提取图像，形成最终的batch（即样本数少的类别有些图像会过采样，但是是上面这种方式来确定哪个图片要过采样）。Label Shuffling方法的优点是只需要原始的batch图片，不需要对整个数据集来做类别平衡。

Bag of Tricks for Convolutional Neural Networks

文章地址：https://arxiv.org/pdf/1812.01187.pdf
高效训练的trick：

• Linear scaling learning rate：即增大batchsize时新的lr=lr（new_batch_size/old_batch_size）。关于这个可以看这篇文章：https://blog.csdn.net/zxyhhjs2017/article/details/79144660 。实际取值时可以取的略小，比如在新的lr基础上开平方，取开方后的值；
• Learning rate warmup：训练刚开始时，所有的参数都是随机值，如果直接使用较大的lr会造成数值的不稳定，所以我们可以先用一个较小的lr，假设我们前m个batches是用来warmup的，我们设置的初始lr为n，那么当为第i个epoch时，学习率设为n（i/m）；
• Zero γ：即Resnet每一个block最后一层的BN层，BN层首先标准化其输出，然后进行尺度的变换，我们现在将尺度变换中的参数γ初始化为0，相当于减少了层数使得初始阶段更加易于训练；
• No bias decay：指weight decay只用于卷积层和FC的weights，biases和BN层的γ和β都不用。

训练方法改进的trick：

• Cosine Learning Rate Decay：Cosine Learning Rate Decay是2016年提出来的，公式如下:
  $${\eta }_t=\frac{1}{2}\left(1+\cos \left(\frac{t\pi }{T}\right)\right)\eta$$
  其中T是总batch数，t是当前batch索引，η是初始学习率。
  从最后的准确率来看，余弦衰减似乎并无优势，也没有加速收敛。
• Label Smoothing：公式如下：
  $$q_i=\{\begin{array}{ll}1-\epsilon & \text{ if }i=y\\ \epsilon /(K-1)& \text{ otherwise }\end{array}$$
  文中取值ε=0.1，K=1000。
• Knowledge Distillation：引入与soft target的loss项，p是ground truth，r是student模型的pred，z是teacher模型的pred。
  $$\ell (p,\text{ softmax }(z))+T^2\ell (\text{ softmax }(r/T),\text{ softmax }(z/T))$$
• Mixup Training：将两个样本及其label做线性加权，得到新样本。

attention module

Squeeze-and-Excitation Networks

文章地址：https://arxiv.org/pdf/1709.01507.pdf
文章思路用下图即可说明清楚：

轻量级的attention模块，参数量和计算量增加很少。作者使用特征图GAP再加上全连接层产生每个channel的权重，然后和原特征图按channel相乘。如果backbone是resnet网络，那么还要将得到的特征图再和原特征图相加。

Selective Kernel Networks

文章地址：https://arxiv.org/pdf/1903.06586.pdf
文章思路看下图：

轻量级的attention模块，参数量和计算量增加很少。作者认为对于不同任务，使用3x3卷积的特征得到的表现和使用5x5卷积的特征的表现并不一样，有些特征需要大一些的卷积核提取出的特征，因此先将两个卷积核提取的特征相加，然后做GAP和FC，再分为两个FC分支，使用softmax进行约束，这样对于两个卷积核的特征就都产生按channel的权重，且同一个channel的权重和为1，最后得到的特征图为两个卷积核的特征按channel权重相加。

Spatial Group-wise Enhance: Improving Semantic Feature Learning in Convolutional Networks

文章地址：https://arxiv.org/pdf/1905.09646.pdf
文章思路可以看下图：

轻量级的attention模块，参数量和计算量增加很少。首先将feature map按channel维度分为G个group，reshape，然后对每个group进行global average pooling得到g向量。g向量与reshape后的feature map进行element-wise dot，再进行norm（注意每个group要学习两个缩放偏移参数使得normalize操作可被还原），之后使用sigmoid进行激活，这样我们得到了这个group的mask，再用这个mask与reshape后的feature map进行element-wise dot即可。最后reshape成（b,c,h,w）。

Non-local Neural Networks

文章地址：https://arxiv.org/pdf/1711.07971.pdf
文章思路可看下图：

卷积是对局部区域进行的操作，所以它们是典型的local操作。受计算机视觉中经典的非局部均值（non-local means）的启发，本文提出一种non-local operations用于捕获长距离依赖（long-range dependencies），即如何建立图像上两个有一定距离的像素之间的联系，如何建立视频里两帧的联系，如何建立一段话中不同词的联系等。
non-local操作在计算某个位置的响应时，是考虑所有位置features的加权，所有位置可以是空间的，时间的，或者空间+时间的。
模块如上图，这也是一个即用即插的模块，可用于分类、检测、分割等任务。

GCNet: Non-local Networks Meet Squeeze-Excitation Networks and Beyond

文章地址：https://arxiv.org/pdf/1904.11492.pdf
文章思路可看下图：


作者先将non local block简化为simple non local block，然后参考SE block的做法提出了GC block（图d）。该block前半部分是Non local block，后半部分是SE block的改进。
相比于SNL，SNL中的transform的1x1卷积在res5中是2048x1x1x2048，其计算量较大，所以借鉴SE的方法，加入压缩因子，为了更好的优化，还加入了layernorm。
相比于SE，一方面是提取的全局信息更加充分（其实这一点在后续的实验中说服力不是很强，单独avg pooling+add，只掉了0.3个点，但是更加简洁），另一方面则是加号和乘号的区别，而且在实验结果上，加号比乘号有显著的优势。
该block可用于分类、检测、分割等任务。

CBAM: Convolutional Block Attention Module

文章地址：https://arxiv.org/pdf/1807.06521.pdf
文章思路可看下图：

文章有两个创新点：一是同时用global average pooling和global max pooling的信息来计算attention模块的权重，二是既在通道上做attention，又在空间位置上做attention。作者通过实验证明先进行通道上的attention，再进行空间位置上的attention效果要比并行做两个attention好。

ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks

文章地址：https://arxiv.org/pdf/1910.03151.pdf
文章思路可看下图：

作者先研究了senet（r为压缩比）：
SE（Global average pooling-FC[r]-ReLu-FC[r]-sigmoid）
SE-Var1（Global average pooling-sigmoid）
SE-Var2（Global average pooling-channel个w与gap点乘-sigmoid）
SE-Var3（Global average pooling-FC-sigmoid）
可以发现只有一层FC的Var3比有两层的SE模块效果更好，这说明不降维对attention模块权重的学习更好。另外，作者认为同其他所有通道交互不如只与附近k个通道的信息进行交互，因此作者设计了ECA模块。该模块先通过下式计算k：
$$k=\psi (C)={\left|\frac{{\log }_2(C)}{\gamma }+\frac{b}{\gamma }\right|}_{odd}$$
其中γ=2，b=1。
然后先进行global average pooling，再用k作为卷积核大小对GAP之后的feature map进行一维卷积，最后与原feature map相乘（channel wise）。

dropout

dropout在前几年往往用在全连接层中，用在卷积层中效果并不明显，原因是卷积层总是卷积一块相邻的空间位置，少掉一两个特征影响并不大。在resnet这样的short cut连接的网络出现之后，dropout使用的场合就越来越少了。
现在除非是数据集太小容易过拟合，否则一般不考虑使用dropout。

Dropout: A Simple Way to Prevent Neural Networks from Overfitting

文章地址：http://jmlr.org/papers/volume15/srivastava14a.old/srivastava14a.pdf
每次更新参数之前，每个特征值有一定的概率被丢弃，假设为p%，p可以设为20或者根据验证集的表现来选取，输入层的p比较小，保留概率接近于1；测试阶段不dropout，保留所有特征值，但是要乘以保留概率1-p%，这是为了保证输出期望一致。
对每个样本都随机地丢弃一部分特征值可以使每个神经元不依赖所有其他神经元来做出决策，这样学习到的特征更加独立。由于每个batch都是随机丢弃特征值，相当于每个batch训练的网络都不一样。与完整的Bagging集成不同，Dropout并不是在整个数据集上完整的训练每个网络架构，而只在一个批次的数据上（min-batch）训练不同的网络架构，因此是一种廉价的Bagging集成近似方法。测试时每个单元乘以保留概率1-p%，这样的效果近似于对多个不同的瘦网络做平均。
Dropout随机丢弃部分特征值，打破了神经元之间相互协作的机制，迫使每个神经元独立的学习更加鲁棒的特征，避免了某些特征只有在其它特征下才有效的情况。因此Dropout类似于L1、L2等正则化效果，通过减少权重提高网络的鲁棒性和泛化能力。

Efficient Object Localization Using Convolutional Networks

文章地址：https://arxiv.org/pdf/1411.4280.pdf
这里我们只看这篇文章最大的motivation：SpatialDropout。
具体可看下图：

dropout是在所有维度上完全随机地丢弃特征值，而SpatialDropout是指定某个channel，然后按比例直接对某个channel上的一组特征值全部丢弃。
如：

原始矩阵shape：(1, 7, 5)
[[[ 0.  2.  4.  6.  8.]
  [ 0.  0. 14. 16. 18.]
  [ 0.  0. 24.  0. 28.]
  [ 0. 32. 34.  0.  0.]
  [40.  0.  0.  0. 48.]
  [ 0. 52.  0. 56.  0.]
  [ 0. 62. 64.  0.  0.]]]
dropout：rate=0.5
[[[ 0.  2.  4.  6.  8.]
  [ 0.  0. 14. 16. 18.]
  [ 0.  0. 24.  0. 28.]
  [ 0. 32. 34.  0.  0.]
  [40.  0.  0.  0. 48.]
  [ 0. 52.  0. 56.  0.]
  [ 0. 62. 64.  0.  0.]]]
SpatialDropout：假如设为(3,1,5)，即在第二个维度上进行SpatialDropout，rate=0.5
[[[ 0.  2.  0.  6.  8.]
  [ 0. 12.  0. 16. 18.]
  [ 0. 22.  0. 26. 28.]
  [ 0. 32.  0. 36. 38.]
  [ 0. 42.  0. 46. 48.]
  [ 0. 52.  0. 56. 58.]
  [ 0. 62.  0. 66. 68.]]]

DropBlock: A regularization method for convolutional networks

文章地址：https://arxiv.org/pdf/1810.12890.pdf
卷积层的特征图中相邻位置元素在空间上共享语义信息，而dropout只随机丢弃单个特征值，但与其相邻的特征值依然可以保有该位置的语义信息，因此dropout对卷积层的效果并不明显。
DropBlock随机Drop一个CHW的特征块（取一个mask点按block_size大小扩展成块）。
下面公式中keep_prob可认为是传统dropout保留激活单元的概率。有效的seed region 为 (feat_size - block_size + 1) 的平方，feat_size 为feature map的size。实际上DropBlock中的dropblock可能存在重叠的区域, 因此上述的公式仅仅只是一个估计。
$$\gamma =\frac{1-kee{p}_{-}prob}{bloc{k}_{-}siz{e}^2}\frac{fea{t}_{-}siz{e}^2}{{\left(fea{t}_{-}size-bloc{k}_{-}size+1\right)}^2}$$

Regularization of Neural Networks using DropConnect

文章地址：http://yann.lecun.com/exdb/publis/pdf/wan-icml-13.pdf
文章思路可看下图：

Dropout在训练过程中以一定概率p将一部分输出值置0，在反向传播更新神经元权重时，由于链式求导法则，与该置0输出值相连的神经元权重不再更新（只是指通过这个输出值的反向传播路径）。
DropConnect与Dropout不同的是，它不是随机将隐含层节点的输出值置0,而是将节点中的每个与其相连的输入权值以p的概率置0。

normalization

四种normalization方法如下图所示。

batch Normalization是在batch上，对NHW做归一化，对小batchsize效果不好；
layer Normalization在通道方向上，对CHW归一化，主要对RNN作用明显；
instance Normalization在图像像素上，对HW做归一化，用在风格化迁移；
Group Normalization是LN和IN的折中，GN在channel方向分group，然后在每个group内归一化；
Switchable Normalization是将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层应该使用什么方法。

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

文章地址：https://arxiv.org/pdf/1502.03167.pdf
深度学习都遵循独立同分布假设，即假设训练数据和测试数据是满足相同分布的，那么通过训练数据获得的模型能够在测试集获得同样的效果。
Batch Normalization用来解决“Internal Covariate Shift”问题。深层神经网络在做非线性变换前的激活输入值（y=wx+b）y随着网络深度加深或者在训练过程中，其分布会逐渐发生偏移或者变动，比如整体分布逐渐往非线性函数的取值区间的上下限两端靠近。如果激活函数是sigmoid函数，此时会导致反向传播时的梯度非常小，即导致梯度消失。
Batch Normalization就是通过一定的规范化，把每层神经网络输入值的分布强行拉回到均值为0方差为1的标准正态分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。
BN是在batch上，对N、H、W做归一化，而保留通道C的维度。BN对batchsize的大小比较敏感，由于每次计算均值和方差是在一个batch上，所以如果batchsize太小，则计算的均值、方差不足以代表整个数据分布；BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用BN很方便，但对于RNN来说计算很麻烦。
算法流程：

• 沿着通道计算每个batch的均值u；
• 沿着通道计算每个batch的方差σ^2；
• 对x做归一化；
  $${\hat{x}}^{(k)}\leftarrow \frac{x_i^{(k)}-{\mu }_{\beta }^{(k)}}{\sqrt{{\sigma }_{\beta }^{(k{)}^2}+ϵ}}$$
• 加入缩放和平移变量γ和β，注意这是两个可学习的参数，归一化后的值为：
  $$y_i^{(k)}\leftarrow {\gamma }^{(k)}{\hat{x}}_i^{(k)}+{\beta }^{(k)}$$

Layer Normalization

文章地址：https://arxiv.org/pdf/1607.06450.pdf
上面说了BN的两个缺点：对batchsize的大小比较敏感和不能用在RNN上。LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。
$${\mu }^l=\frac{1}{H}\sum _{i=1}^H{a}_i^l{\sigma }^l=\sqrt{\frac{1}{H}\sum _{i=1}^H{\left(a_i^l-{\mu }^l\right)}^2}$$
layerNorm在通道方向上，对CHW归一化，可以使用在RNN上。
LN中同层神经元输入拥有相同的均值和方差，Layer Normalization在单条数据内部就能归一化，不同的输入样本有不同的均值和方差；BN中则针对不同神经元输入计算均值和方差，同一个batch中的输入拥有相同的均值和方差；LN不依赖于batch size和输入sequence的长度，因此可以用于batch size为1和RNN中。LN用于RNN效果比较明显，但是在CNN上，效果不如BN。

Instance Normalization:The Missing Ingredient for Fast Stylization

文章地址：https://arxiv.org/pdf/1607.08022.pdf
Instance NormalizationIN针对图像像素做normalization，最初用于图像的风格化迁移。在图像风格化中，生成结果主要依赖于某个图像实例，feature map 的各个channel的均值和方差会影响到最终生成图像的风格。所以对整个batch归一化不适合图像风格化迁移任务，因此对H、W做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。
$$y_{tijk}=\frac{x_{tijk}-{\mu }_{ti}}{\sqrt{{\sigma }_{ti}^2+ϵ}},{\mu }_{ti}=\frac{1}{HW}\sum _{l=1}^W\sum _{m=1}^H{x}_{tilm},{\sigma }_{ti}^2=\frac{1}{HW}\sum _{l=1}^W\sum _{m=1}^H{\left(x_{tilm}-m{u}_{ti}\right)}^2$$

Group Normalization

文章地址：https://arxiv.org/pdf/1803.08494.pdf
Group Normalization是为了解决BN对较小的mini-batch size效果差的问题。GN适用于占用显存比较大的任务，例如图像分割。对这类任务，可能batch size只能是个位数，再大显存就不够用了。当batch size是个位数时，BN的表现很差，因为没办法通过几个样本的数据量，来近似总体的均值和标准差。GN也是独立于batch的，它是LN和IN的折中。
Group Normalization在channel方向分group，然后在每个group内做Norm，计算（C//G）HW的均值和方差，这样就与batch size无关，不受其约束。

Differentiable Learning-to-Normalize via Switchable Normalization

文章地址：https://arxiv.org/pdf/1806.10779.pdf
目前已有的Normalization方法：BN是沿着所有样本的同一个通道计算，它首先应用在图像分类任务中，有助于提高收敛速度和泛化性；LN是对单个样本的特征进行计算，它首先应用在RNN中，使得RNN的优化更容易；IN是对每个样本的每个通道计算，首先应用在风格转换任务上，基于它可以解决任意风格的转换的问题；GN与LN类似，只是在对通道进行了分组，它解决了BN对于batch size的依赖问题。
作者提出自适配归一化方法——Switchable Normalization（SN），将BN、LN、IN结合，赋予权重，让网络自己去学习每一个归一化层应该使用什么方法。
SN算法是为三组不同的uk和σk分别学习三个总共6个标量值wk和wk’， 最后计算的是它们的加权和：
$${\hat{h}}_{ncij}=\gamma \frac{h_{ncij}-{\sum }_{k\in \Omega }{w}_k{\mu }_k}{\sqrt{{\sum }_{k\in \Omega }{w}_k^{\prime }{\sigma }_k^2+ϵ}}+\beta$$
$$\Omega =\{in,ln,bn\}$$
$${\mu }_{in}=\frac{1}{HW}\sum _{i,j}^{H,W}{h}_{ncij},{\sigma }_{in}^2=\frac{1}{HW}\sum _{i,j}^{H,W}{\left(h_{ncij}-{\mu }_{in}\right)}^2$$
$${\mu }_{ln}=\frac{1}{C}\sum _{c=1}^C{\mu }_{in},{\sigma }_{ln}^2=\frac{1}{C}\sum _{c=1}^C\left({\sigma }_{in}^2+{\mu }_{in}^2\right)-{\mu }_{ln}^2$$
$${\mu }_{bn}=\frac{1}{N}\sum _{n=1}^N{\mu }_{in},{\sigma }_{bn}^2=\frac{1}{N}\sum _{n=1}^N\left({\sigma }_{in}^2+{\mu }_{in}^2\right)-{\mu }_{bn}^2$$
wk是通过softmax计算得到的激活函数：
$$w_k=\frac{e^{{\lambda }_k}}{{\sum }_{z\in in,ln,bn}{e}^{{\lambda }_z}}\text{ and }k\in \{in,ln,bn\}$$
λin，λbn，λln需要优化的3个参数，可以通过BP调整它们的值。同理我们也可以计算wk’对应的三个参数。
在BN的测试过程中，为了计算其归一化统计量，传统的BN方法是从训练过程中利用滑动平均的方法得到的均值和方差。在SN的BN部分，它使用的是一种叫做批平均（batch average)的方法，它分成两步：

• 固定网络中的SN层，从训练集中随机抽取若干个批量的样本，将输入输入到网络中；
• 计算这些批量在特定SN层的μ和σ的平均值，它们将会作为测试阶段的均值和方差。

实验结果表明，在SN中批平均的效果略微优于滑动平均。

Two at Once: Enhancing Learning and Generalization Capacities via IBN-Net

文章地址：https://arxiv.org/pdf/1807.09441.pdf
模块结构可看下图：

在cross domain问题中，在浅层的bn层替换为in+bn层，这是因为in层可以保留feature的外观差异性，而bn层保证了样本总体数据分布的一致性。在网络深层时，由于此时特征主要是高级语义信息，此时只用bn层，不用in层。IBN-a即在resnet的每一个block的第一个conv中加上in，并保留一半的bn，且只加载前三个block中。最后一个stage的block仍然只使用bn；IBN-b即在resnet的每一个block的residual做了element wise add后加入in，且只在第一个conv和前两个block后。
本方法适合用在reid这类跨域问题中。

knowledge distillation

Do Deep Nets Really Need to be Deep?

文章地址：https://arxiv.org/pdf/1312.6184.pdf
深层网络真的需要很深吗？对于参数一样的深层网络和浅层网络，如果都是从头开始训练，深层网络的性能通常比浅层网络好，但是当我们使用深层网络蒸馏浅层网络时，最终性能基本相同。
如何蒸馏？浅层网络不使用one hot label，而使用深层网络生成的logit作为训练目标， 这是softmax之前的值。为什么不用softmax之后的值呢？因为不同的logit softmax之后的值可能一样，而且可能会让网络把注意力集中在较大的值上，忽略了对较小值的学习。

Distilling the Knowledge in a Neural Network

文章地址：https://arxiv.org/pdf/1503.02531.pdf
我们使用交叉熵损失函数让模型学习样本时，由于样本标签是one hot编码，因此不是1就是0，模型从样本上学习不到一个样本中不同类之间的关系。
softmax公式：
$$q_i=\frac{\exp \left(z_i/T\right)}{{\sum }_j\exp \left(z_j/T\right)}$$
温度参数T通常设置为1，T越大可以得到更“软”的概率分布。
本文提出的蒸馏方法是先训练一个点数较高的大模型。然后训练小模型时，使用两项损失函数，一项是样本和小模型预测的交叉熵，另一项是大模型预测（按温度系数T）和小模型预测的交叉熵函数，将一般按0.5比0.5分配权重，不同任务可能比例不同。
实际实现时往往采用这种形式：第一项为小模型本身的交叉熵函数，第二项为KL散度：
$$D_{KL}(p\Vert q)=\sum _{i=1}^{N}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right)$$
即大模型和小模型的最后一个fc层输出先过按温度系数T的softmax层，然后按上式计算KL散度。最后，KL散度前要乘以T的平方。

FITNETS: HINTS FOR THIN DEEP NETS

文章地址：https://arxiv.org/pdf/1412.6550.pdf
本文说明了如何从一个wide and deep的网路蒸馏成一个thin and deeper的网络。在使用kd loss的基础上，同时使用L2 loss蒸馏中间层feature map。

Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer

文章地址：https://arxiv.org/pdf/1612.03928.pdf
文章提出用attention map代替feature map，再使用l2 loss进行蒸馏。有两种attention map：activation-based and gradient-based。文中实验中认为有效的是activation-based attention map。
有三种形式：
$$\begin{array}{l}\bullet \text{ sum of absolute values: }{F}_{\text{sum }}(A)={\sum }_{i=1}^C\left|A_i\right|\\ \bullet \text{ sum of absolute values raised to the power of }p(\text{ where }p>1):F_{\text{sum }}^p(A)={\sum }_{i=1}^C{\left|A_i\right|}^p\\ \bullet \text{ max of absolute values raised to the power of }p(\text{ where }p>1):F_{\text{max }}^p(A)={\max }_{i=1,C}{\left|A_i\right|}^p\end{array}$$
三种形式在不同任务中往往有一到两种可以比直接使用feature map取得更好的蒸馏效果。

Like What You Like: Knowledge Distill via Neuron Selectivity Transfer

文章地址：https://arxiv.org/pdf/1707.01219.pdf
本文的创新点在于将l2 loss更改为以下形式：
$${\mathcal{L}}_{{\mathrm{M}\mathrm{M}\mathrm{D}}^2}(\mathcal{X},\mathcal{Y})={\Vert \frac{1}{N}\sum _{i=1}^N\varphi \left({\mathbf{x}}^i\right)-\frac{1}{M}\sum _{j=1}^M\varphi \left({\mathbf{y}}^j\right)\Vert }_2^2$$
φ（·）为核函数，文中实验表明二项式核函数的效果最好。

Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons

文章地址：https://arxiv.org/pdf/1811.03233.pdf
本文提出一种新的蒸馏方法：只蒸馏激活位置（大于0的值的位置），而不是像l2 loss各个位置值分布保持一致。
核心公式：
$$\mathcal{L}(\mathbf{I})=\Vert \rho (\mathcal{T}(\mathbf{I}))-\rho (\mathcal{S}(\mathbf{I})){\Vert }_1$$
由于这个公式不可微分，所以改成下面这种形式：
$$\begin{array}{rl}\mathcal{L}(\mathbf{I})=& \Vert \rho (\mathcal{T}(\mathbf{I}))\odot \sigma (\mu 1-\mathcal{S}(\mathbf{I}))+(1-\rho (\mathcal{T}(\mathbf{I})))\odot \sigma (\mu 1+\mathcal{S}(\mathbf{I})){\Vert }_2^2\end{array}$$

A Comprehensive Overhaul of Feature Distillation

文章地址：https://arxiv.org/pdf/1904.01866v1.pdf
这篇文章讨论了蒸馏的位置，以前蒸馏总是蒸馏ReLU之后的feature map，这篇文章选择蒸馏每个stage最后一个bolck ReLU之前的feature map。
由于教师feature map的特征值是ReLU之前的值，因此正值是有价值的信息，而负值不是。如果教师中的特征值为正，则学生必须产生与教师中相同的特征值。相反，如果教师的特征值为负，则学生也应产生小于零的值。同时作者提出教师的特征值蒸馏前需要过一个margin ReLU激活函数，这个函数会将小于一定值的负值转为临界的负值。对于教师margin ReLU后的负值，如果学生的特征值高于该值，则应该减少，但如果学生的特征值低于该值，则不需要增加，因为经过ReLU后都会变成0。

On the Efficacy of Knowledge Distillation

文章地址：https://arxiv.org/pdf/1910.01348.pdf
本文证明了一些观点：

• 更好的老师不一定能教出更好的学生，老师和学生之间的gap增大到一定程度后，学生无法更准确的模仿老师，表现出来就是KD损失变得更大，蒸馏效果变差；
• 在蒸馏后期，早一些停止蒸馏，仅使用分类loss进行最后一个阶段的模型训练有助于使分类loss最小化，使得模型最终准确率更高。如果KD loss和CE loss一起使用，在后期KD loss会干扰CE loss的最小化，使模型效果变差；
• 如果学生和老师差距太大，可以先用老师训一个更小一点的老师，再用这个老师训练学生。

REVISIT KNOWLEDGE DISTILLATION: A TEACHERFREE FRAMEWORK

文章地址：https://arxiv.org/pdf/1909.11723.pdf
本文提出了一些观点：

• 知识蒸馏是一种可学习的标签平滑，是一种正则化；
• 标签平滑可以看成一种生硬的知识蒸馏；
• 随着温度T的增大，知识蒸馏中教师soft label的分布越来越接近标签平滑的均匀分布。

A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning

文章地址：http://openaccess.thecvf.com/content_cvpr_2017/papers/Yim_A_Gift_From_CVPR_2017_paper.pdf
本文不使用KD loss，也不蒸馏中间层feature map，而是蒸馏每个stage开始的feature map和每个stage结束时的feature map之间的相关性，这个相关性用一个gram矩阵来表示，称为FSP矩阵。
实现方式是大模型先使用FSP矩阵蒸馏小模型，然后小模型只用CE loss进行训练。

Similarity-Preserving Knowledge Distillation

文章地址：https://arxiv.org/pdf/1907.09682.pdf
本文将feature map reshape为（b，chw），然后乘以其转置，得到一个gram矩阵，这个矩阵表示两两样本间的相似性。由于gram矩阵不太稳定，所以对其每一行做l2 norm，然后对teacher和student的gram矩阵做l2 loss进行蒸馏。因此本文蒸馏的是样本间的相关性。
事实上，这个loss也可以和KD loss配合使用。

Correlation Congruence for Knowledge Distillation

文章地址：https://arxiv.org/pdf/1904.01802.pdf
和上文比较类似，使用gram矩阵样本间相关性，使用KD loss蒸馏每个样本信息，两者配合使用，gram矩阵再使用一个非线性核映射一下，弥补样本间的非线性关系。从实验结果来看，这样蒸馏后类内更紧密，但这依赖于教师网络是否能学习到更紧密的类内关系。

When Does Label Smoothing Help?

文章地址：https://arxiv.org/pdf/1906.02629.pdf
本文研究了label smooth。
label smooth会使倒数第二层的激活函数与正确分类间的差值减小，并使其与正确和错误分类的距离等同；label smooth能够有效防止模型过拟合；如果对教师网络进行标签平滑，虽然教师网络的性能提升了，但是蒸馏得到的学生网络性能会变得更差，这可能是因为标签平滑减少了类间相互信息。

cnn module

卷积计算与全连接计算的异同

3x3卷积与全连接计算的异同：
假设输入10x10x3的特征图，输出10x10x1的特征图。batchsize为1。
全连接层输入10x10x3的特征图，首先将其reshape成一维的300个输入值，然后输出reshape成10x 10x1的形状。全连接层的参数为（300，100）的矩阵。
如果我们要使卷积层完全等价于全连接层，我们需要使用100个10x10x3的卷积核，卷积后得到100个输出值，再reshape成10x10x1的形状。卷积核参数共100x10x10x3个。因此全连接层可以看成是核很大的卷积层。
如果我们使用3x3x3大小的卷积核，stride = 1， 为了输出分辨率不变padding用SAME方式。输出通道数为1，即只有一个3x3x3大小的卷积核，输出也为10x10x1的特征图。全连接层输入10x10x3=300个神经元，而3x3卷积的时候每次卷积只是连接了其中的一个3x3x3=27的子集，那么可以在做全连接的时候，除了这27个神经元设置非零链接系数，其余的300-27=273个连接系数直接设置为0就可以了。做10x10x1=100次这样的全连接，就可以得到100个输出神经元，再reshape成10x10x1的形状。
也就是说，卷积层可以看成是一种稀疏的全连接层。
1x1卷积与全连接计算的异同：
假设输入10x10x3的特征图，输出10x10x1的特征图。batchsize为1。
全连接层输入10x10x3的特征图，首先将其reshape成一维的300个输入值，然后输出reshape成10x 10x1的形状。全连接层的参数为（300，100）的矩阵。
1x1卷积层输入10x10x3的特征图，使用1x1x3的卷积核，输出为10x10x1的特征图，只需要1个1x1x3的卷积核，结论与上面类似。
假设输入为1x1x512的特征图，输出1x1x3的特征图。batchsize为1。
全连接层输入1x1x512的特征图，首先将其reshape成一维的512个输入值，然后输出reshape成1x1x3的形状。全连接层的参数为（512，3）的矩阵。
使用1x1x512的卷积核，一共需要3个这样的卷积核，得到输出也是1x1x3的特征图。1x1卷积的参数量为512x3。

Network In Network

文章地址：https://arxiv.org/pdf/1312.4400.pdf
global average pooling:
最后一层输出的特征图对每个通道上的特征图做全局池化，得到一个（channels,1）的特征向量，再送入softmax中进行计算。使用global average pooling来代替全连接层，是为了使最后一个卷积层获得的每一个特征图能够对应于一个输出类别。全连接层非常容易导致过拟合，极度依赖dropout。global average pooling没有参数需要进行优化，因此可以避免在这一层出现Overfitting。
例如CIFAR-100分类任务，直接将最后一层卷积层channel设为100，对每个feature map（共100个）进行global average pooling得到100维的输出向量，对应100种图像分类。
1x1卷积：
实质上是在不改变feature map的h和w的同时进行跨channel的信息融合，可以在减少channel的数量的同时将原本所有channel的信息融合到更少的channel中。

Making Convolutional Networks Shift-Invariant Again

文章地址：https://arxiv.org/pdf/1904.11486.pdf
不具有平移不变性一直是CNN存在的问题，这是由于pooling和stride conv下采样带来的问题。目前大多数的解决方法是靠数据增广来缓解，但是数据增强不可能覆盖所有平移幅度的样本空间。这篇Adobe的工作通过引入Blur conv来缓解CNN对平移的混淆问题。
举例：假如输入为(0,0,1,1,0,0,1,1,0,0),如果max pooling的size为2，得到的结果是(0,1,0,1,0)，如果输入平移一格，输出则为(1,1,1,1)。经过多次pool之后，平移等方差的偏差会变得越来越大。故网络越深，降采样越多，对平移越敏感。
作者创造了一种blurpool来解决这个问题。先使用2x1的窗口取max操作，然后使用一个模糊滤波器作为卷积核对特征图做一次卷积操作，最后再进行下采样。如下图所示：

Adaptively Connected Neural Networks

文章地址：https://arxiv.org/pdf/1904.03579.pdf
本文提出了一种新的网络模块：ACnet。ACNet考虑了三种信息：自映射、局部信息、全局信息。ACnet给三种信息赋予相同的初始化权重（通过softmax约束），然后通过网络的训练来学习这些权重。
ACnet公式如下：
$${\mathbf{y}}_i={\alpha }_i\sum _{j=i}{\mathbf{x}}_j{\mathbf{u}}_{ij}+{\beta }_i\sum _{j\subseteq N(i)}{\mathbf{x}}_j{\mathbf{v}}_{ij}+{\gamma }_i\sum _{\forall j}{\mathbf{x}}_j{\mathbf{w}}_{ij}$$
其中xj表示输入数据。α，β和γ在所有通道中共享，且α+β+γ=1。第一项代表自信息（CNN网络后接1x1卷积），第二项代表CNN网络信息（CNN网络后接3x3卷积），第三项代表全局信息（CNN输出后接全连接结果）。
三项分别是CNN网络输出结果通过一个1x1的卷积，CNN网络输出结果通过一个3x3的卷积，和CNN网络输出结果通过一个经过全局平均池化的全连接，分别乘上一个可学习的权重后得到最终的结果。
第三项全连接非常耗费计算量，因此首先通过全局平均池化操作对x进行变换。最后，上式获得的y可以通过非线性函数f激活，例如BatchNorm + ReLU。
α是通过使用具有λα作为控制参数的softmax函数来计算的，其可以通过标准反向传播（BP）来学习：
$$\alpha =\frac{e^{{\lambda }_{\alpha }}}{e^{{\lambda }_{\alpha }}+e^{{\lambda }_{\beta }}+e^{{\lambda }_{\gamma }}}$$
类似地，β和γ分别通过使用另一个参数λβ和λγ来定义。

Deep Layer Aggregation

文章地址：https://arxiv.org/pdf/1707.06484.pdf
作者研究了类似resnet这样由许多结构相似的block堆叠成的网络在block和stage级别的特征融合方式。一种方式是IDA（iterative deep aggregation）迭代深度融合，即不同stage输出的特征的融合（往往channel、height、width都不相同），另一种方式是HDA（hierarchical deep aggregation）分层深度聚合，即输出了同样的channel、height、width的feature map之间的融合，往往是一个stage内前后不同block输出的feature map之间的融合。
融合结构如下：

作者在ResNet、ResNeXT、DenseNet上均作了实验，都取得了增益效果。

Deformable Convolutional Networks

文章地址：https://arxiv.org/pdf/1703.06211.pdf
Deformable Convolution的结构可看下图：


本文提出了可变形卷积和可变形ROI poling。其原理就是学习一个偏移变量（x,y），使卷积核在采样点发生偏移，从而改变了感受野的范围。
具体来说，使用deformable convolution时，先用一个卷积层得到一个2N的offset field，N就是通道数，field的H和W和feature map相同，这样HxWxN的feature map就得到了一个HxWx2N的offset filed，对应与feature map上每个点有两个偏移量（x,y）。在实际当中，因为添加的这个偏移量往往是小数，导致比较难处理，作者采用的办法是用双线性差值来计算。当然这种卷积的计算速度比平常的卷积要慢。

classification loss

Focal Loss for Dense Object Detection

文章地址：https://arxiv.org/pdf/1708.02002.pdf
文章最大的创新在于Focal loss的提出及 one stage目标检测网络RetinaNet（Resnet + FPN + FCN）。
二分类的交叉熵公式:
$$\mathrm{C}\mathrm{E}(p,y)=\{\begin{array}{ll}-\log (p)& \text{ if }y=1\\ & \\ -\log (1-p)& \text{ otherwise }\end{array}$$
现在假设一个pt变量来代替上面交叉熵公式的两种情况:
$$p_{\mathrm{t}}=\{\begin{array}{ll}p& \text{ if }y=1\\ & \\ 1-p& \text{ otherwise }\end{array}$$
则：
$$\mathrm{C}\mathrm{E}\left(p_{\mathrm{t}}\right)=-\log \left(p_{\mathrm{t}}\right)$$
这个公式和上面的交叉熵公式其实是一样的。
再进一步对公式进行改造，得到focal loss公式:
$$\mathrm{F}\mathrm{L}\left(p_{\mathrm{t}}\right)=-{\left(1-p_{\mathrm{t}}\right)}^{\gamma }\log \left(p_{\mathrm{t}}\right)$$
这个时候的pt就具有了控制易分类样本和难分类样本的权重的作用。 pt越大代表越容易分类，那么1-pt越小，y是一个整数指数，指数化之后就更小了。这样越简单的样本loss的权重就越小。实际上我们一般使用focal loss时采用的是这个形式。
论文中最后还给focal loss再加上一个αt来控制正负样本的比重：
$$\mathrm{F}\mathrm{L}\left(p_{\mathrm{t}}\right)=-{\alpha }_{\mathrm{t}}{\left(1-p_{\mathrm{t}}\right)}^{\gamma }\log \left(p_{\mathrm{t}}\right)$$
当y=1时，αt=α; 当y=0时，αt=1-α。这样当y=0（即背景类）时，随着α的增大，会对损失进行很大惩罚（降低权重），从而减轻背景类样本太多对训练的影响。

Gradient Harmonized Single-stage Detector

文章地址：https://arxiv.org/pdf/1811.05181.pdf
在focal loss的基础上改进的GHM-C loss。focal loss为难样本和简单样本赋予了不同的权重，但是在不同的数据集中，难样本和简单样本的数据分布不一定是一致的，这使得我们在用focal loss时需要对超参数γ进行调参，很不方便。本文提出了一种GHM-C loss，它通过计算每个batch中难样本和简单样本的梯度（label-pred），通过梯度的数量分布为难样本和简单样本赋予一个权重，这样就不需要超参数γ了。
公式如下：
梯度的绝对值：
$$g=\left|p-p^{\ast }\right|=\{\begin{array}{ll}1-p& \text{ if }{p}^{\ast }=1\\ p& \text{ if }{p}^{\ast }=0\end{array}$$
梯度密度函数：
$$GD(g)=\frac{1}{l_{ϵ}(g)}\sum _{k=1}^N{\delta }_{ϵ}\left(g_k,g\right)$$
梯度密度函数表示一个batch的样本中梯度落在某个梯度区间内的样本数量。
协调参数：
$${\beta }_i=\frac{N}{GD\left(g_i\right)}$$
N表示一个batch的样本数。
则有：
$$\begin{array}{rl}{L}_{GHM-C}& =\frac{1}{N}\sum _{i=1}^N{\beta }_i{L}_{CE}\left(p_i,p_i^{\ast }\right)\\ & =\sum _{i=1}^N\frac{L_{CE}\left(p_i,p_i^{\ast }\right)}{GD\left(g_i\right)}\end{array}$$
该函数直接计算所有的样本的梯度密度分布的时间复杂度为O（N2），而通过先排序再统计梯度的方式，时间复杂度为O（NlogN）。本篇论文通过简化求出近似的梯度密度分布来加快计算，实验表明，性能上只有极其微小损失。
把X轴划分为M个区域，落在每个区域内的样本采用同一个权重X轴的梯度分为M个区间，每个区间长度为ε，第j个区域为rj，用Rj表示落在第j个区域内的样本数量。定义ind（g）表示梯度为g的样本所落区域的序号，即可得出新的参数 [公式] 和新的GHM-C loss函数。
$$\widehat{GD}(g)=\frac{R_{ind(g)}}{ϵ}=R_{ind(g)}M$$
$${\hat{\beta }}_i=\frac{N}{GD\left(g_i\right)}$$
$$\begin{array}{rl}{\hat{L}}_{GHM-C}& =\frac{1}{N}\sum _{i=1}^N{\hat{\beta }}_i{L}_{CE}\left(p_i,p_i^{\ast }\right)\\ & =\sum _{i=1}^N\frac{L_{CE}\left(p_i,p_i^{\ast }\right)}{GD\left(g_i\right)}\end{array}$$
由于样本的梯度密度是训练时根据batch计算出来的，通常情况下batch较小，直接计算出来的梯度密度可能不稳定，所以采用滑动平均的方式处理梯度计算。
$$S_j^{(t)}=\alpha S_j^{(t-1)}+(1-\alpha )R_j^{(t)}$$
$$\widehat{GD}(g)=\frac{S_{ind(g)}}{ϵ}=S_{ind(g)}M$$
GHM的思想同样可以用于anchor的坐标回归，这里就不细说了。

Class-Balanced Loss Based on Effective Number of Samples

文章地址：https://arxiv.org/pdf/1901.05555.pdf
一种用于多类别平衡的loss函数，适用于类别比较多（大于等于100类）的情况。在类别比较多的时候，各个类别的样本数量分布接近于长尾分布。
传统的类别平衡方法有如类平衡损失与样本量成反比，但是表现并不是太好；还有与类别数量的平方根成反比，相比于前者则更加平滑；如果为难样本分配更高权重，则更容易学习到有害样本（如噪音，错标的数据）。
本文公式如下：
$$\beta =(N-1)/N$$
$${\mathrm{C}\mathrm{B}}_{\mathrm{f}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}(\mathbf{z},y)=-\frac{1-\beta }{1-{\beta }^{ny}}\sum _{i=1}^C{\left(1-p_i^t\right)}^{\gamma }\log \left(p_i^t\right)$$
其实就是在focal loss前加了一个平衡类别的权重，ny为每个类别的样本数量。对于样本量比较多的类别，得到的权重接近1/类别数；对于样本量很少的类别，得到的权重会被一定程度上放大。这个loss适合100类以上的多分类问题。

A New Loss Function for CNN Classifier Based on Pre-defined Evenly-Distributed Class Centroids

文章地址：https://arxiv.org/ftp/arxiv/papers/1904/1904.06008.pdf
预先生成一组类中心（代替原来的全连接层，也就是说全连接层初始化成某个特征的参数，然后冻结，只train网络其他部分）。预定义最优随机聚类中心的方式是一个超球体上人为地设定很多均匀分布的点，假设这些点是不同的类，这些聚类中心的距离都是最远的，每个点是高维的。然后只train网络其他部分，把不同类别的样本分别映射到这些预定义类的中心，然后对它们进行聚类。这样可以最大限度地分离不同类之间的距离。
论文中生成预定义类中心的方法：基于球面上的同性电荷能量最低的物理模型，即假设超球面上的n个电荷点相互之间有排斥力，排斥力随点间的距离增加而减少，当运动最后平衡，超球上的点停止运动时，由于斥力的存在，N个点最后会在超球面上均匀分布，达到平衡状态时就可以使超球面上的 N个点相距最远。我们定义中心点的每一维都有一个Vi运动量，来描述运动状态，每一步计算更新所有点的运动状态。
我们用预定义的以类为中心（PEDCC权重）替换卷积神经网络的最后一层，并且在训练阶段，仅更新先前层的权重。loss函数为两部分，一部分是全连接后softmax后计算cosface loss，另一部分是平方误差函数，n=1。
PEDCC loss：
$$L_{PEDCC-AM}=-\frac{1}{N}\sum _i\log \frac{e^{s\cdot \left(\cos {\theta }_{y_i}-m\right)}}{e^{s\cdot \left(\cos {\theta }_{y_i}-m\right)}+{\sum }_{j=1,j\ne y_i}^c{e}^{s\cdot \cos {\theta }_j}}$$
$$L_{PEDCC-MSE}=\frac{1}{2}\sum _{i=1}^m{\Vert x_i-{\mathrm{pedcc}}_{y_i}\Vert }^2$$
$$L=L_{PEDCC-AM}+\sqrt[n]{L_{PEDCC-MSE}}$$

CosFace: Large Margin Cosine Loss for Deep Face Recognition

文章地址：https://arxiv.org/pdf/1801.09414.pdf
对于原始的softmax函数，最后softmax的每个神经元权重乘以特征向量可以分解为如下形式：
$$W_j^{T}x=\Vert W_j\Vert \Vert x\Vert \cos {\theta }_j$$
即神经元的权重向量的模和特征向量的模相乘，再乘以两个向量夹角的余弦值，这是简单的向量点积的基本定义公式。该公式表明，向量的范数和角度都有助于后验概率。
在测试阶段，通常根据两个特征向量之间的余弦相似度来计算测试面对的面部识别得分。这表明特征向量x的范数对loss函数没有贡献。因此在训练阶段乘以一个s来进行补偿。固定x的范数s可以去除直径方向的变化，所以得到的模型学习到在角度空间中可分离的特征。然后我们要让余弦值减去一个m，使得模型学习到的不同类别的特征空间相互分离的更远。
最后的损失函数公式：
$$L_{lmc}=\frac{1}{N}\sum _i-\log \frac{e^{s\left(\cos \left({\theta }_{y_i,i}\right)-m\right)}}{e^{s\left(\cos \left({\theta }_{y_i,i}\right)-m\right)}+{\sum }_{j\ne y_i}{e}^{s\cos \left({\theta }_{j,i}\right)}}$$
$$\begin{array}{rl}W& =\frac{W^{\ast }}{\Vert W^{\ast }\Vert }\\ x& =\frac{x^{\ast }}{\Vert x^{\ast }\Vert }\\ \cos \left({\theta }_j,i\right)& =W_j^T{x}_i\end{array}$$

AdaptiveFace: Adaptive Margin and Sampling for Face Recognition

文章地址：http://www.cbsr.ia.ac.cn/users/xiangyuzhu/papers/2019adaptiveface.pdf
reading+1
将softmax中的margin由原来的超参数变为可学习的参数。
之前的margin-based softmax loss如cosface中设置margin参数确实可以减小类内方差，扩大类间方差，但是没有考虑到样本不均衡的问题。对于一个二分类问题，假设类1的样本量较小，类2的样本量较大，那么类1样本的样本方差必然与类1的实际方差差距较大（样本方差较小）。由于cosface对所有类别使用同一个margin，对于样本量较少且类内方差较小的类，loss对该类的特征空间压缩的不够。因为该类的样本量少，样本的方差小，但也由于样本量少，其样本方差比实际方差要小，也就是说该类真实的特征空间要更大一些。但模型只能通过样本学习，学习到的是样本的特征空间分布，因此与真实的特征空间分布差距较大。
作者提出的AdaM-Softmax分配更大的margin来进一步压缩样本量少的类１的特征空间，其真实的特征空间被进一步压缩了。
原始cosface公式：
$$L_{lmc}=-\frac{1}{M}\sum _{j=1}^M\log \frac{e^{s\left(\cos \left({\theta }_y(j{)}_j\right)-m\right)}}{e^{s\left(\cos \left({\theta }_y(j{)}_j\right)-m\right)}+{\sum }_{i=1,i\ne y}^N{e}^{s\cos \left({\theta }_{ij}\right)}}$$
改进后：
$$L_{ad}=-\frac{1}{M}\sum _{j=1}^M\log \frac{e^{s\left(\cos \left({\theta }_y(j{)}_j\right)-m_y(j)\right)}}{e^{s\left(\cos \left({\theta }_y(j{)}_j\right)-m_y(j)\right)}+{\sum }_{i=1,i\ne y}^N{e}^{s\cos \left({\theta }_{ij}\right)}}$$
即每个类别有一个可学习的margin。
由于自己学出来的margin有可能为0，而m希望得到一个更大的值，作者对损失函数也进行了改进：
$$L_m=-\frac{1}{N}\sum _{i=1}^N{m}_i$$
$$L_{AdaM}=L_{ad}\pm \lambda \ast L_m$$

Sharpen Focus: Learning with Attention Separability and Consistency

文章地址：https://arxiv.org/pdf/1811.07484.pdf
因为我们预测一张图片中只有一个类，因此我们将预测的最大值代表的类和次大值代表的类（最容易混淆的类）它们两个的Grad-CAM heatmap区域分离开，并保持中间层和最后层中heatmap的定位尽量一致。
loss函数：
$$L=L_C+L_{AS}^{in}+L_{AS}^{la}+L_{AC}$$
Lc即普通的交叉熵函数。
$$L_{AS}=2\cdot \frac{{\sum }_{ij}\left(\min \left({\mathcal{A}}_{ij}^T,{\mathcal{A}}_{ij}^{Conf}\right)\cdot {\mathrm{Mask}}_{ij}\right)}{{\sum }_{ij}\left({\mathcal{A}}_{ij}^T+{\mathcal{A}}_{ij}^{Conf}\right)}$$
$${\mathrm{Mask}}_{ij}=\frac{1}{1+\exp \left(-\omega \left({\mathcal{A}}_{ij}^T-\sigma \right)\right)}$$
$$L_{AC}=\theta -\frac{{\sum }_{ij}\left({\mathcal{A}}_{ij}^{in}\cdot {\mathrm{Mask}}_{ij}\right)}{{\sum }_{ij}{\mathcal{A}}_{ij}^{in}}$$
σ为0.55，ω为100，θ为0.8。

object detection

object detection model

Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks

文章地址：https://arxiv.org/pdf/1506.01497.pdf
第一篇使用Anchor的二阶段目标检测器。所谓Anchor，就是在feature map上每个点的一组固定长宽的先验框。对于faster rcnn，就是9个先验框（三种尺度大小和三种长宽比）。网络训练分为两个阶段，即训练RPN和后面的分类+回归网络。RPN也是分类+回归两个分支，只是RPN的分类是二分类（目标or背景），而后面的分类是对目标的具体细分类。注意训练RPN时，由于背景框远远多于目标框，因此在所有的检测框中，挑选出128个positive与128个negative，用于训练。当正例的检测框小于128个时，使用negative进行填充。这256个框的选取，可以在检测框置信度排序、nms、超出边界过滤之后，随机选取。
两个阶段的损失函数都可以用下面的公式表达：
$$L\left(p_i,t_i\right)=\frac{1}{N_{cls}}\sum _i{L}_{cls}\left(p_i,p_i^{\ast }\right)+\lambda \frac{1}{N_{reg}}\sum _i{p}_i^{\ast }{L}_{reg}\left(t_i,t_i^{\ast }\right)$$
分类使用的是softmax损失函数，而回归使用的是smooth l1损失函数。
smooth l1损失函数公式如下：
$${\mathrm{smooth}}_{L_1}(x)=\{\begin{array}{cc}0.5x^2& \text{ if }|x|<1\\ |x|-0.5& \text{ otherwise }\end{array}$$
回归时并不是直接回归坐标，而是回归tx,ty,tw,th：
$$\begin{array}{rl}{t}_x& =\left(x-x_a\right)/w_a\\ t_y& =\left(y-y_a\right)/h_a\\ t_w& =\log \left(w/w_a\right)\\ t_h& =\log \left(h/h_a\right)\end{array}$$

每个anchor ground truth的分配：对每个目标，IoU大于0.7的anchor分配为这个目标的正样本（单个目标可能分配多个anchor为正样本）。若这个目标没有IoU大于0.7的anchor，则取IoU最大的那个anchor作为这个目标的正样本。对于与所有目标IoU都小于0.3的anchor分配为负样本。剩下的anchor均忽略，不参与训练。retinanet的anchor ground truth分配规则与上面一样，只是分配正负样本的IoU阈值取值不同。

Feature Pyramid Networks for Object Detection

文章地址：https://arxiv.org/pdf/1612.03144v2.pdf
FPN结构用下面两张图就可以说明白：


将backbone网络每个block的最后一层特征图命名为C2，C3，C4，C5，将高层特征做2倍的上采样（最近邻上采样法），然后和前一层特征图做element-wise add。得到的M2，M3，M4，M5再经过3x3卷积得到P2，P3，P4，P5。每个P层只处理单一的尺度信息。对32、64、128、256、512这五种尺度的anchor，分别对应到P2、P3、P4、P5、P6这五个特征层上。每个特征层都处理1:1、1:2、2:1三种长宽比例的候选框。

You Only Look Once: Unified, Real-Time Object Detection

文章地址：https://arxiv.org/pdf/1506.02640.pdf
本文即YOLOv1，第一个单阶段目标检测器。文章核心思想：把检测和分类都看成回归问题，从而实现单阶段目标检测器。
文章模型可看下图：

YOLOv1把backbone最后输出的feature map上的每个点看成对应于原始图像上的一片区域。加入最后的feature map是SxS的，那么就相当于把原始图像切分成SxS个格子。每个格子输出B个bounding box（包含物体的矩形区域）信息，以及C个物体属于某种类别的概率信息，在文章中B=2。
Bounding box包含5个数据，分别是x，y，w，h和confidence。其中xy是指当前格子预测得到的物体的bounding box的中心位置的坐标。wh指bounding box的宽度和高度。在训练时，为了防止收敛困难，w和h使用图像的宽度和高度进行归一化到[0,1]区间内，xy则转化为bounding box中心位置相对于当前格子位置的偏移值，也被归一化到[0,1]。
confidence反映当前bounding box是否包含物体以及物体位置的准确性，公式如下：
$$\mathrm{Pr}(\text{Object})\times {\text{IOU}}_{\text{pred}}^{\text{truth}},\mathrm{Pr}(\text{Object})\in \{0,1\}$$

若bounding box包含物体，则P(object) = 1；否则P(object) = 0。在测试时，这个框的confidence要与类预测相乘，然后将小于阈值的框去除，剩余的框再经过NMS过滤。
损失函数公式如下：
$$\begin{array}{r}{\lambda }_{\text{coord }}\sum _{i=0}^{S^2}\sum _{j=0}^B{1}_{ij}^{\text{obj }}\left[{\left(x_i-{\hat{x}}_i\right)}^2+{\left(y_i-{\hat{y}}_i\right)}^2\right]\\ +{\lambda }_{\text{coord }}\sum _{i=0}^{S^2}\sum _{j=0}^B{1}_{ij}^{\text{obj }}\left[(\sqrt{w_i}-\sqrt{{\hat{w}}_i}{)}^2+(\sqrt{h_i}-\sqrt{{\hat{h}}_i}{)}^2\right]\\ +\sum _{i=0}^{S^2}\sum _{j=0}^B{1}_{ij}^{\text{obj }}{\left(C_i-{\hat{C}}_i\right)}^2\\ +{\lambda }_{\text{noobj }}\sum _{i=0}^{S^2}\sum _{j=0}^B{1}_{ij}^{\text{noobj }}{\left(C_i-{\hat{C}}_i\right)}^2\\ +\sum _{i=0}^{S^2}{1}_i^{\text{obj }}\sum _{c\in \text{ classes }}{\left(p_i(c)-{\hat{p}}_i(c)\right)}^2\end{array}$$
如果一个物体的中心落在某个单元格上，那么这个单元格负责预测这个物体。只有有物体的格子，才用于回归训练（损失函数前两项）；有物体的格子回归训练有物体的概率（损失函数第三项）；没有物体的格子回归训练没有物体的概率（损失函数第四项）；有物体的格子回归训练分类概率（损失函数第五项）。

YOLOv3: An Incremental Improvement

文章地址：https://pjreddie.com/media/files/papers/YOLOv3.pdf
YOLOv3使用了Anchor，anchor是按照YOLOv2中聚类得到的9个anchor（九个框分别是 (10×13)，(16×30)，(33×23)，(30×61)，(62×45)，(59× 119)， (116 × 90)， (156 × 198)，(373 × 326)）。YOLOv3也使用了FPN，有三个层级。把9个anchor按照面积从小到大排列，每个层级的feature map上的每个点有3个Anchor。
损失函数如下：
$$\begin{array}{c}\mathrm{los}{s}_{N_1}={\lambda }_{box}{\sum }_{i=0}^{N_1\times N_1}{\sum }_{j=0}^3{1}_{ij}^{obj}\left[{\left(t_x-t_x^{\prime }\right)}^2+{\left(t_y-t_y^{\prime }\right)}^2\right]\\ +{\lambda }_{box}{\sum }_{i=0}^{N_1\times N_1}{\sum }_{j=0}^3{1}_{ij}^{obj}\left[{\left(t_w-t_w^{\prime }\right)}^2+{\left(t_h-t_h^{\prime }\right)}^2\right]\\ -{\lambda }_{obj}{\sum }_{i=0}^{N\times N}{\sum }_{j=0}^3{1}_{ij}^{obj}\log \left(c_{ij}\right)\\ -{\lambda }_{\text{noobj }}{\sum }_{i=0}^{N_1\times N_1}{\sum }_{j=0}^3{1}_{ij}^{\text{noobj }}\log \left(1-c_{ij}\right)\\ -{\lambda }_{\text{class }}{\sum }_{i=0}^{N_1\times N_1}\\ {\sum }_{j=0}^3{1}_{ij}^{obj}{\sum }_{c\in \text{ classes }}\left[p_{ij}^{\prime }(c)\log \left(p_{ij}(c)\right)+\left(1-p_{ij}^{\prime }(c)\right)\log \left(1-p_{ij}(c)\right)\right]\end{array}$$
总的损失函数是三个FPN层级上的损失函数之和：
$$\text{Loss}={\mathrm{loss}}_{N_1}+{\mathrm{loss}}_{N_2}+{\mathrm{loss}}_{N_3}$$
分类损失函数是多个二分类的sigmoid损失函数。如果一个anchor是负样本，那么不计算回归损失和分类损失。如果一个anchor是正样本，则上面五项损失函数都参与计算。

检测框的解码：

sigmoid(tx)和sigmoid(ty)是基于矩形框中心点左上角格点坐标的偏移量，pw和ph是先验框的宽、高，cx和cy是当前方格距离图片左上角的距离，通过上述公式，计算出实际预测框的宽高bw和bh 。
ground turth的分配：首先每个物体的中心都会落在确定的一个格子里，不存在物体的格子里的先验框全部忽略，不会用于训练。对于存在物体的格子，有3个先验框，IoU最高的为正样本，小于某个IoU阈值的全部为负样本，这个格子的其他框忽略，不用来训练（每个物体只会分配一个正样本的anchor）。如果这个格子内所有框都小于这个阈值，则取最高IoU的框为正样本，其他为负样本。YOLOv3需要假定每个cell至多含有一个grounth truth，而在实际上基本不会出现多于1个的情况。

Focal Loss for Dense Object Detection

文章地址：https://arxiv.org/pdf/1708.02002.pdf
文章最大的创新在于Focal loss的提出及单阶段目标检测网络RetinaNet。
二分类的交叉熵公式:
$$\mathrm{C}\mathrm{E}(p,y)=\{\begin{array}{ll}-\log (p)& \text{ if }y=1\\ & \\ -\log (1-p)& \text{ otherwise }\end{array}$$
现在假设一个pt变量来代替上面交叉熵公式的两种情况:
$$p_{\mathrm{t}}=\{\begin{array}{ll}p& \text{ if }y=1\\ & \\ 1-p& \text{ otherwise }\end{array}$$
则：
$$\mathrm{C}\mathrm{E}\left(p_{\mathrm{t}}\right)=-\log \left(p_{\mathrm{t}}\right)$$
这个公式和上面的交叉熵公式其实是一样的。
再进一步对公式进行改造，得到focal loss公式:
$$\mathrm{F}\mathrm{L}\left(p_{\mathrm{t}}\right)=-{\left(1-p_{\mathrm{t}}\right)}^{\gamma }\log \left(p_{\mathrm{t}}\right)$$
这个时候的pt就具有了控制易分类样本和难分类样本的权重的作用。 pt越大代表越容易分类，那么1-pt越小，y是一个整数指数，指数化之后就更小了。这样越简单的样本loss的权重就越小。实际上我们一般使用focal loss时采用的是这个形式。
论文中最后还给focal loss再加上一个αt来控制正负样本的比重：
$$\mathrm{F}\mathrm{L}\left(p_{\mathrm{t}}\right)=-{\alpha }_{\mathrm{t}}{\left(1-p_{\mathrm{t}}\right)}^{\gamma }\log \left(p_{\mathrm{t}}\right)$$
当y=1时，αt=α; 当y=0时，αt=1-α。这样当y=0（即背景类）时，随着α的增大，会对损失进行很大惩罚（降低权重），从而减轻背景类样本太多对训练的影响。

retinanet的结构非常简洁，一个resnet50/101 backbone+5级FPN（P3，P4，P5，P6，P7），然后接一个分类分支和一个定位分支。分类分支使用多个二分类的sigmoid focal loss(bce loss乘以两个权重），只计算正负anchor样本（还有一部分anchor被忽略）。定位分支使用和faster rcnn一样的smooth l1 loss，只计算正anchor样本，注意定位分支预测的四个值是tx/ty/tw/th，完全和faster rcnn一样。

FCOS: Fully Convolutional One-Stage Object Detection

文章地址：https://arxiv.org/pdf/1904.01355.pdf
文章模型可看下图：

FCOS是一个anchor free的单阶段目标检测器。它以resnet作为backbone，也使用了fpn，后面接分类、回归和center_ness三个分支。检测器没有使用anchor，而是把fpn每层的feature map上的每一个点看成一个样本，当点落入某个目标的真实框内就是正样本（类别即这个目标的类），否则就是负样本。除此之外，回归的四个参数l，t，r，b也与retinanet不同，指的是这个点到框四条边的距离。由于回归目标l，t，r，b都是正的，作者使用exp函数将其映射到范围（0，正无穷）。

损失函数：
$$L\left(p_{x,y}{t}_{x,y}\right)=\frac{1}{N_{pos}}\sum _{x,y}{L}_{cls}\left(p_{x,y},c_{x,y}^{\ast }\right)+\frac{\lambda }{N_{pos}}\sum _{x,y}{1}_{(c_{x,y}^{\ast }>0)}{L}_{reg}\left(t_{x,y},t_{x,y}^{\ast }\right)$$
该loss函数包含两部分，Lcls表示分类loss，本文使用的是Focal_loss（类别损失）；Lreg表示回归loss，本文使用的是IOU loss。px,y表示特征图的位置（x,y）处的分类概率，tx,y表示特征图的位置（x,y）处的回归坐标。Npos表示正样本的个数，在这篇论文中λ=1用于平衡Lreg的权重。对特征图Fi上的各个位置的结果进行求和再除以正样本的数量。

在FCOS中，检测器在特征图的不同层级上检测不同大小的物体，作者使用了特征图的5种层级，即P3、P4、P5、P6、P7。由于多个目标的重叠区域会造成训练目标的不明确，对于真实框重叠区域中的点，采用下面的办法处理。首先在所有特征层上的每个位置计算回归目标:
$$l^{\ast },t^{\ast },r^{\ast },b^{\ast }$$
如果一个位置满足:
$$\max \left(l^{\ast },t^{\ast },r^{\ast },b^{\ast }\right)>m_i或\max \left(l^{\ast },t^{\ast },r^{\ast },b^{\ast }\right)<m_{i-1}$$
那么它就被设为负样本，就不需要回归。mi是第i个特征层需要回归的最大距离。在论文中，m2、m3、m4、m5、m6、m7分别被设为0、64、128、256、512、∞。作者发现在数据集中多个目标的重叠一般来说这多个目标的尺度大小差异很大，因此通过上面的操作可以把不同大小的对象分到不同的fpn层级上。另外，如果这样分以后仍然有重叠，那么把这个点分配给面积最小的真实框目标。

Center-ness：
使用FPN后，FCOS的性能仍然低于基于anchor的检测器。因此作者又提出了center-ness分支来抑制检测出的低质量检测框。
对于给定的一个位置的回归目标:
$$l^{\ast },t^{\ast },r^{\ast },b^{\ast }$$
center-ness中心度表示从位置到该位置所负责的对象中心的标准化距离，定义如下:
$$centernes{s}^{\ast }=\sqrt{\frac{\min \left(l^{\ast },r^{\ast }\right)}{\max \left(l^{\ast },r^{\ast }\right)}\times \frac{\min \left(t^{\ast },b^{\ast }\right)}{\max \left(t^{\ast },b^{\ast }\right)}}$$
使用根号是为了降低centerness衰减的速度。center-ness（中心度）取值为0到1之间，通过二元sigmoid交叉熵损失来训练。并把这个损失加入前面提到的损失函数中。测试时，将预测的center-ness和对应的分类得分相乘，得到最终的得分，再用这个得分对检测边框进行排名。因此center-ness可以降低那些远离物体中心边框的得分。在最后的NMS过程中，这些低质量的边框就会很大概率上被剔除，从而显着提高了检测性能。

Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection

文章地址：https://arxiv.org/pdf/2006.04388.pdf
在目前最新的单阶段检测器FCOS和ATSS中，检测框的质量估计都使用center-ness。还有一些单阶段检测器使用IOU作为检测框的质量估计。但是，classification score 和 IoU/centerness score 训练和测试并不一致。在训练时，分类分支和质量估计分支各自独立的训练，但测试时却乘在一起，这样就会存在一定的gap。另外，分类分支使用focal loss训练，包含正样本和负样本，但是回归分支却只使用正样本进行训练。这样就必然会存在一部分分数较低的负样本的质量预测是没有在训练过程中得到训练，因此有可能出现这种情况：一个分类score相对低的真正的负样本，由于预测了一个不可信的极高的质量score，而导致它可能排到一个真正的正样本（分类score不够高且质量score相对低）的前面。另外，在实际场景中，边界框的表示具有很强的不确定性，而现有的框回归本质都是建模了非常单一的狄拉克分布，这不一定和实际场景吻合。
本文根据这两个问题提出了QFL loss和DFL loss解决。
QFL loss:
$$QFL=-|y-\sigma {|}^{\beta }((1-y)\log (1-\sigma )+y\log (\sigma ))$$
其中y是乘以iou以后的smooth label（原始为1），sigma是分类预测的Pred。beta是超参数，在本文中设为2。
使用QFL loss替换原始的focal loss，这样网络在学习时就能根据预测框的质量来平滑分类label。比如说如果iou只有0.5，那么这个分类label的真值就是1x0.5。
对于建模任意分布来表示回归框，以往的giou loss就属于这样的尝试。但由于分布如果是任意的，则网络的学习效率不高，涨点有限。考虑到真实的分布通常不会距离标注的位置太远，所以作者额外增加了 DFL loss，希望网络能够快速地聚焦到标注位置附近的数值。
DFL loss:
$$DFL\left({\mathcal{S}}_i,{\mathcal{S}}_{i+1}\right)=-\left(\left(y_{i+1}-y\right)\log \left({\mathcal{S}}_i\right)+\left(y-y_i\right)\log \left({\mathcal{S}}_{i+1}\right)\right)$$
最后，QFL和DFL其实可以统一地表示为GFL（Generalized Focal Loss），公式如下：
$$GFL\left(p_{y_l},p_{y_r}\right)=-{\left|y-\left(y_l{p}_{y_l}+y_r{p}_{y_r}\right)\right|}^{\beta }\left(\left(y_r-y\right)\log \left(p_{y_l}\right)+\left(y-y_l\right)\log \left(p_{y_r}\right)\right)$$
网络的总体损失函数如下：
$$L=\frac{1}{N_{\text{pos}}}\sum _z{\mathcal{L}}_{QFL}+\frac{1}{N_{\text{pos}}}\sum _z{1}_{\left\{c_z^{\ast }>0\right\}}\left({\lambda }_0{\mathcal{L}}_{GIOU}+{\lambda }_1{\mathcal{L}}_{DFL}\right)$$
需要说明的是，QFL这个函数也可以用在如retinanet这些单阶段目标检测器上。

Bottom-up Object Detection by Grouping Extreme and Center Points

文章地址：https://arxiv.org/pdf/1812.01187.pdf
文章模型可看下图：

本文检测的不是目标框(长方形)的四个对角线端点，而是四个极值点和一个中心点。中心点很好理解就是目标框的中心点。由于我们的框应当恰好框住物体，所以框的每一条边上应该有一部分与物体的外边缘重合，所谓的四个极值点就是每条边上在物体的外边缘上的点。这样避免了类似Cornernet这类网络在检测角点时目标框的角点落在背景中的问题。
首先和Cornernet一样使用hourglass作为backbone网络提取特征图,然后对要预测的四个极值点和一个中心点并行地预测五个heatmap，并对四个极值点分别还预测一个offset分支拟合前面特征图下采样时下取整产生的误差。然后暴力枚举所有四种极值点的组合，计算每种组合中心点的位置，如果中心点的heatmap上对应位置上的响应超过预设阈值，则将这一组5个点作为一个备选，该备选组合的score为5个对应点的score平均值。
暴力枚举的时间复杂度O（n^4），不过n一般非常小，所以影响不大。
文中提到一种问题:处理三个共线且尺度相同的目标时，是产生三个正确的小框还是一个错误的大框呢？比如在三车道上并行地平行行驶的汽车。
作者使用soft NMS来处理这种情况：如果某个边框中包含的所有框的分数之和超过其本身得分的3倍，则将其得分除以2。
基于四个极值点的实例分割:
文中提出了一个简单的八边形逼近目标的方法，将一个极值点左右各延长1/8形成线段，如果遇到矩形框的角时则截断。将这四个线段的端点连接起来，形成八边形。

Matrix Nets: A New Deep Architecture for Object Detection

文章地址：https://arxiv.org/pdf/1908.04646.pdf
文章模型可看下图：


该网络由三部分组成。首先用backbone提取特征图，然后使用Matrix Net网络得到不同宽高比和尺寸的特征图，再后面和centernet类似，预测左上角点、右下角点、中心点和offset，最终计算出目标位置。
Matrix Net中每向右一层特征图宽度减半，每向下一层特征图高度减半。对角线层则宽高都减半。每个特征图的宽高比和尺寸均不同，这使得方形卷积核可以收集不同宽高比的信息。

Receptive Field Block Net for Accurate and Fast Object Detection

文章地址：https://arxiv.org/pdf/1711.07767.pdf
本文作者主要是创建了一种新的模块来代替现有的卷积层。模块结构如下：

人类的视觉系统是由多个具有不同感受野的部分复合而成的。而不同的感受野对于整个图像上的信息敏感度并不是平均的，越靠近中心的部分越重要。作者从中得到灵感，设计了Receptive Field Block。
该block采用多个不同大小卷积核层并行的机构，这与Inception模块类似，但是与Inception模块不同的是，Inception中所有的不同大小的卷积核其采样中心点是相同的。而作者认为卷积核越大，则采样点应该离中心点越远，应该尽可能地分布的比较散而不是像Inception一样不同大小的卷积核其采样中心都一样。作者通过调节空洞卷积的rate来调节不同大小的卷积核的离心率实现了这一点，比如5x5卷积层的采样点和到中心的距离就比3x3和1x1的更远。
1x1的卷积和Inception中作用类似，也是用于减少计算量和进行跨通道信息融合。1x3和3x1的卷积也是用于减少计算量的。RFBs使用了较多的小卷积核，除了运算量方面的考虑，也更适合关注比较局部的信息，适合用在比较浅的层。

Deep High-Resolution Representation Learning for Human Pose Estimation

文章地址：https://arxiv.org/pdf/1902.09212.pdf
本文即HRnetv1网络。网络结构如下：

在整个过程中保持高分辨率的特征表示，逐步增加High-to-Low的子网，并将多分辨率的子网并行连接；在并行的多分辨率子网之间反复交换信息，进行多尺度融合，高分辨率特征与低分辨率特征之间相互增强。整个网络分为4个stage，每个stage比上一个stage多一条分支，新增分支是对上一个stage所有特征图进行strided convolution融合后的结果，分辨率大小是上一个分支分辨率大小的一半，通道数翻倍，每个stage由mutil-resolution block组成。 每一个mutil-resolution block又分为两部分：multi-resolution group convolution是若干条并行的分支，每条分支上包含4个残差单元；multi-resolution convolution进行多尺度特征融合。对于HRNetV1，最后只输出高分辨率特征图。

High-Resolution Representations for Labeling Pixels and Regions

文章地址：https://arxiv.org/pdf/1904.04514.pdf
本文即HRNetv2网络。网络结构如下：

HRNet即high resolution Net（高分辨率网络）。low resolution net就是之前的分类网络，通过stride逐步减少分辨率，获取语义信息，最终得到分类，比如resnet。但是这种low-resolution net对于目标检测或者语义分割来说是不可兼容的，因为语义分割最终需要的结果是high-resolution的，也就是每个pixel的class。
目前获得high-resolution的网络有两种方式：

• 第一种是类似于encoder-decoder的网络，如U-net，SegNet等，就是先使用down-sampling降低resolution获取语义信息，再通过upsample增加resolution获得空间信息；
• 第二种是整个网络都保持high-resolution，并且使用平行线路来得到low-resolution，如GrideNet，HRnet。

HRNet是一个通用的特征提取网络，可以用于分类、检测、分割等。网络在前向计算时随着stage改变不断增加更低分辨率的分支，并且在每个stage结束时并行的高低分辨率网络以类似全连接的方式进行信息融合。
在HRNetv1中，在最后一个stage时，只有最高分辨率的特征图被输出。这意味着只有高分辨率子通道的信息被利用，其他通道的信息被舍去了。在HRNetv2中，作者对低分辨率的特征图进行双线性上采样，然后在channel上concate起来，这样就利用了所有分辨率的特征图的信息。

IoU

什么是IoU

IoU即交并比，是目标检测中最常用的指标，用来衡量预测框和ground-truth的差别有多大。公式如下：
$$IoU=\frac{|A\cap B|}{|A\cup B|}$$
它反映了预测框与真实框的差别有多大，另外IoU有一个特性就是对框的尺度大小不敏感。
但是，作为损失函数，它也有缺点。一是如果预测框和真实框完全不相交，IoU=0，不能反映两者的距离远近。而是相同的重合度下，框的重合效果也是不一样的，如：

上图中三种情况下IoU都相等，但显然左边的图检测框效果最好，右边的图效果最差。

Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

文章地址：https://arxiv.org/pdf/1902.09630.pdf
本文即GIOU loss。由于IoU对框的尺度不敏感，但是检测任务中的BBox回归损失（MSE loss, l1-smooth loss等）的优化和IoU优化不是完全等价的，且Ln范数对物体的尺度也比较敏感，传统的IoU无法直接优化没有重叠的部分。本文提出可以把GIoU作为回归的loss。GIoU公式如下：
$$GIoU=IoU-\frac{\left|A_c-U\right|}{\left|A_c\right|}$$
Ac为同时包含预测框和真实框的最小闭包框的面积，然后计算Ac中不覆盖预测框或检测框的面积占Ac的比值，再用IoU减去这个比值得到GIoU。
与IoU类似，GIoU也可以作为一个距离，loss可以用下式来计算：
$$L_{GIoU}=1-GIoU$$
GIoU同样对框的尺度不敏感。同时，在两个框完全不重合时，IoU=GIoU=0。IoU取值为[0,1]，GIoU取值范围[-1,1]。在两者完全重合的时候取最大值1，在两者无交集且无限远的时候取最小值-1，因此GIoU是一个非常好的距离度量指标。与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。

Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

文章地址：https://arxiv.org/pdf/1911.08287.pdf
IoU loss和GIoU loss仍然存在收敛速度慢和回归不准确的问题。当IoU为0时，GIoU会先尽可能让预测框和目标框产生相交，产生相交后GIoU loss退化为IoU loss，此时会和IoU loss一样存在收敛速度慢和回归不准确的问题。
基于上面的问题，本文提出直接最小化预测框和真实框之间的归一化距离，即DIoU loss：
$$DIoU=IoU-\frac{{\rho }^2\left(b,b^{gt}\right)}{c^2}$$
其中b和bgt分别代表了预测框和真实框的中心点，p代表两个中心点的欧式距离，c代表同时包含预测框和真实框的最小闭包框的对角线距离。因此，DIoU中对预测框和真实框之间的归一化距离进行了建模。
和GIoU Loss类似，DIoU Loss在预测框和真实框不重叠时，仍然可以尽快让预测框和真实框相交。由于DIoU Loss可以直接最小化两个框的距离，因此比GIoU Loss收敛快得多。对于当预测框包含在目标框内（在水平方向和垂直方向上）的情况，DIoU Loss可以使回归Loss下降的很快，而GIoU Loss此时退化为IoU Loss。DIoU还可以在NMS中替换普通的IoU，使NMS的结果更加合理。
那么，如何使回归 loss在预测框与真实框相交或包含时收敛的更快更准呢？作者提出了CIoU Loss（Complete-IoU Loss）。作者认为一个预测框与真实框的差距应该从三个方面进行考虑：相交面积、中心距离、长宽比。GIoU解决了IoU为0时不能优化的问题。DIoU考虑了相交面积和中心点距离。作者在DIoU的基础上再考虑了预测框长宽比和真实框长宽比之间的差距，得到了CIoU Loss：
$${\mathcal{L}}_{CIoU}=1-IoU+\frac{{\rho }^2\left(\mathbf{b},{\mathbf{b}}^{gt}\right)}{c^2}+\alpha v$$
$$v=\frac{4}{{\pi }^2}{\left(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w}{h}\right)}^2$$
$$\alpha =\frac{v}{(1-\mathrm{IoU})+v}$$
其中a是用来平衡比例的系数，v用来衡量预测框长宽比和真实框长宽比之间的差距。
对w和h求导公式如下：
$$\frac{\partial v}{\partial w}=\frac{8}{{\pi }^2}(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w}{h}$$