最长回文子序列（LPS + 滚动优化）模板

 

问题描述

回文序列(Palindromic sequence, Palindrome)是指正向遍历和反向遍历完全相同的序列，例如字符串“AAAAA”显然是一个回文序列，又如字符串“ABC@CBA”也是一个回文序列。现在，我们要在一个（字符）序列中找出最长回文子序列的长度。例如字符序列"BBABCBCAB"，最长回文子序列是“BACBCAB”（可能不唯一），它的长度是7；子序列"BBBBB"和"BBABB"虽然也是回文序列，但却不是最长的，因此不合题意。

字符子串和字符子序列的区别

字符字串指的是字符串中连续的n个字符；如palindrome中，pa，alind，drome等都属于它的字串

而字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符；如palindrome中，plind，lime属于它的子序列，而mod，rope则不是，因为它们与字符串的字符顺序不一致。

分析

对任意字符串，如果头和尾相同，那么它的最长回文子序列一定是去头去尾之后的部分的最长回文子序列加上头和尾。如果头和尾不同，那么它的最长回文子序列是去头的部分的最长回文子序列和去尾的部分的最长回文子序列的较长的那一个。

str[0...n-1]是给定的字符串序列，长度为n，假设f(0,n-1)表示序列str[0...n-1]的最长回文子序列的长度。

1.如果str的最后一个元素和第一个元素是相同的，则有：f(0,n-1)=f(1,n-2)+2；例如字符串序列“AABACACBA”，第一个元素和最后一个元素相同，其中f(1,n-2)表示红色部分的最长回文子序列的长度；

2.如果str的最后一个元素和第一个元素是不相同的，则有：f(0,n-1)=max(f(1,n-1),f(0,n-2))；例如字符串序列“ABACACB”，其中f(1,n-1)表示去掉第一元素的子序列，f(0,n-2)表示去掉最后一个元素的子序列。

 设字符串为s，f(i,j)表示s[i..j]的最长回文子序列。 

状态转移方程如下： 

当i>j时，f(i,j)=0。 

当i=j时，f(i,j)=1。 

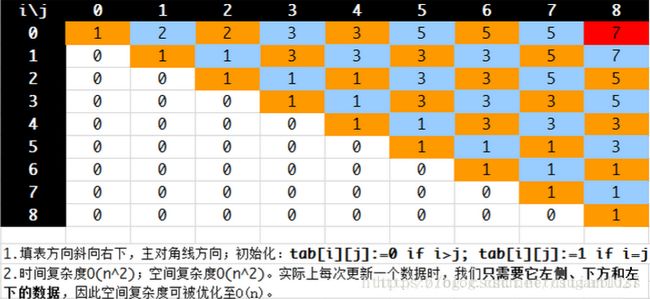
当i

当i

由于f(i,j)依赖i+1，所以循环计算的时候，第一维必须倒过来计算，从s.length()-1到0。 

最后，s的最长回文子序列长度为f(0, s.length()-1)。

以"BBABCBCAB"为例：

（注：本程序的填表方向斜向左上，即每次从最后一行最后一个数开始，依次向左填写）

代码

（时间复杂度O（n^2）），空间复杂度O（n^2））

#include 
#include 
using namespace std;
int dp[1500][1500];
int main()
{
    string str;
    while(cin >> str)
    {
        int len = str.length();

        memset(dp,0,sizeof(dp));

        for(int i = len - 1; i >= 0; i--)
        {
            dp[i][i] = 1;
            for(int j = i + 1; j < len; j++)
            {
                if(str[i] == str[j])
                    dp[i][j] = dp[i+1][j-1] + 2;
                else
                    dp[i][j] = max(dp[i][j-1],dp[i+1][j]);
            }
        }
        cout<

 

为进一步减小空间复杂度，我们发现计算第i行时只用到了第i+1行，这样我们便不需要n行，只需要2行即可。

#include 
#include 
using namespace std;
int dp[2][1500];
int main()
{
    string str;
    while(cin >> str)
    {
        int len = str.length();

        memset(dp,0,sizeof(dp));
        int cur = 0;
        for(int i = len - 1; i >= 0; i--)
        {
            cur ^= 1;
            dp[cur][i] = 1;
            for(int j = i + 1; j < len; j++)
            {
                if(str[i] == str[j])
                    dp[cur][j] = dp[cur^1][j-1] + 2;
                else
                    dp[cur][j] = max(dp[cur][j-1],dp[cur^1][j]);
            }
        }
        cout<