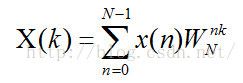C语言实现基2DIF-FFT算法（桑德·图基快速傅立叶变换）

傅立叶变换能将时域信号转换为由sin函数为基底的频域信号，从而我们可以从信号中提取出频率信息或截断频谱简化信号压缩信息。计算机难以处理连续信号。DFT是一种适用于计算机处理的有限信号时频转换方法。DFT用一句话概括，就是将连续信号（频域也是连续函数）经过时域采样（这样会使信号的频域发生周期延拓，得到周期连续的函数，计算机无法处理），再经过频域采样（这样会使时域信号发生周期延拓，时域周期延拓这一步可以直接在采样后实现，即 直接将采样后的DTFT过程转化为DFS），得到周期离散的频谱结果，取主值（一个周期），即得DFT结果X(k)。若要对DFT有个更直观的理解，推荐这篇博客

 

实现DFT的过程，可以总结为计算以下公式的过程

                                                                         (1)

式中，。计算(1)式的朴素算法时间复杂度为O(N^2)，而目前的快速傅立叶算法能使(1)式的时间复杂度降为O( Nlog2(N) )。快速傅立叶算法的思路，就是利用复指数函数的性质减小计算量。一种快速傅立叶算法的思路是将N点DFT转化为N/2点DFT，即 将N点序列进行分割。若按n域(时域)划分，就是所谓DIT-FFT算法(decimation-in-time FFT，库利·图基算法)；按k域(频域)划分，则是DIF-FFT算法(decimation-in-frequency FFT，桑德·图基算法)。本文介绍DIF-FFT算法。将(1)式按k分割成k为奇数和k为偶数两个部分，如下所示:

                                               (2)

                                                                (3)

                                                     (4)

式中，k为偶数用2m代替，k为奇数用2m+1代替。因此，可以依据(3)(4)将N点DFT化为2个N/2点DFT（注意，k为奇数则需要乘上）。最后可以一直化为1点DFT，只有1个点时代入(1)式，X(k)就是x(0)。在这个过程中，以k的奇偶情况，X(k)被分成两簇，原本0到N-1的顺序给打乱了，最后求得的结果中，X(k)的下标分别为0到N-1的位顺序翻转(reversal bits)。4点DIF-FFT算法可用如下例子演示：

 

                                        

                                                                                           图 1

 

FFT适合用位运算进行优化。

DIF-FFT算法C语言程序(mingw编译)：

/*==================================*说明*===================================== 
-创建 fft_in.txt ，将序列输入并保存。运行程序后fft的模值结果输出在 
fft_out.txt-序列最大长度为8192 
=============================================================================*/
#include  
#include 
#include 
#define PI 3.1415926535898
int N,v,j;
double x[8197][2][2], wn[8197][2];

void input();
void fft();
void output();
int bitReversal(int i);

int main(){ 
  input(); 
  fft(); 
  output();
}

void fft(){ 
  //采用桑德-图基蝶形算法(DIF-FFT)实现快速傅立叶变换 
  int st,j1,i,i1,t,m; 
  double tmp,a,b,w,v; //计算Wn 
  for (i=0;i>1;++i){ 
    tmp = 2.0 * PI * i / N; 
    wn[i][0] = cos(tmp); //Wn的实部 
    wn[i][1] = -sin(tmp); //Wn的虚部 
    //printf("%.4f + %.4f i\n", wn[i][0], wn[i][1]); 
  } 
  //计算sigma(i:0->N-1)[x(n)*(Wn^i*k)] 
  m = 1; 
  for (st=N>>1;st>0;st>>=1){
    j1 = j; j = j^1; 
    for (i=0;i 0; 
      i1 = i + st - t * st * 2; 
      x[i][j][0] = x[i1][j1][0]+(1-2*t)*x[i][j1][0]; 
      x[i][j][1] = x[i1][j1][1]+(1-2*t)*x[i][j1][1]; 
      if (t) { 
        //复数乘法 
        w = x[i][j][0]; 
        v = x[i][j][1]; 
        i1 = (i % st) * m; 
        a = wn[i1][0]; 
        b = wn[i1][1]; 
        x[i][j][0] = w * a - v * b; 
        x[i][j][1] = v * a + w * b; 
      } 
      //printf("[i,j]=%d %d x[i,j]=%.4f + %.4f i\n",i,j,x[i][j][0],x[i][j][1]); 
    } 
    m <<= 1; 
  }
}

void input(){ 
  FILE *fp; 
  N = 0; 
  fp=fopen("fft_in.txt","r"); 
  if (fp == NULL) { 
    printf("File cannot be opened.\n"); 
    exit(1); 
  } 
  while (!feof(fp)){
    if (N>8192) {      
      printf("The number of data is out of range.\n");
      fclose(fp);      
      exit(1);    
    }  
    fscanf(fp,"%lf", &x[N][0][0]); 
    //fscanf(fp,"%lf", &x[N][0][1]); 
    N++; 
  } 
  fclose(fp); 
  v = (int)ceil(log(1.0*N)/log(2.0)); 
  N = pow( 2, v ); //为序列补零，使序列长度是2的幂次 
}

void output(){ 
  int i,k; 
  double mag; 
  FILE *fp; 
  fp = fopen("fft_out.txt","w"); 
  for (i=0;i>= 1){ 
    n <<= 1; 
    n |= i & 1; 
    ++t; 
  } 
  n = n << (v-t); 
  return n;
}

 

 

程序输出结果为X(k)的模。

在计算过程中尽量使用位运算，可以提高程序效率，减小代码量。

例如对于4点DIF-FFT，在将4点DFT转化为2点DFT过程中，用

t = (st & i) > 0;

判断是减法还是加法（对照图1可看出）。即 将0到3转化为二进制： 00 01 10 11. 只有当最高位为1时需要减法，所以i & 4 > 0 (st==4) 即可判断。

程序还有很大的优化空间。例如reversal bits的计算，这里点击打开链接 有更快的实现方法。