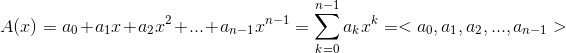Design and Analysis of Algorithms (Divide & Conquer: FFT)

Polynomial operations and representations

A polynomial A(x) can be written in the following form:

 

The degree of A is n-1;

Operations on polynomials

1. Evaluation: Given a polynomial A(x) and a number x0, compute A(x0). This can be done in O(n) time using O(n) arithmetic operations via Horner’s rule
2. Add: This takes O(n) time using basic arithmetic, because ck = ak + bk.
3. Multiplication: Given two polynomials A(x) and B(x), compute C(x) = k A(x)·B(x) (∀x). Then ck = j=0 aj bk−j for 0 ≤ k ≤ 2(n−1), because the degree of the resulting polynomial is twice that of A or B. This multiplication is then equivalent to a convolution of the vectors A and reverse(B). The convolution is the inner product of all relative shifts, an operation also useful for smoothing etc. in digital signal processing.
   • Naive polynomial multiplication takes O(n2).
   • O(n^lg3) or even O(n^(1+ε)) (∀ε > 0) is possible via Strassen-like divide-andconquer tricks.
   • Today, we will compute the product in O(n log n) time via Fast Fourier Transform!

Representations of polynomials

First, consider the different representations of polynomials, and the time necessary to complete operations based on the representation.

1. Coefficient vector with a monomial basis
2. Roots and a scaling term
3. Samples: (x0, y0), (x1, y1), ..., (xn−1, yn−1) with A(xi) = yi (∀i) and each xi is distinct. These samples uniquely determine a degree n − 1 polynomial A, according to the Lagrange and Fundamental Theorem of Algebra. Addition and multiplication can be computed by adding and multiplying the yi terms, assuming that the xi’s match. However, evaluation requires interpolation.

The runtimes for the representations and the operations are described in the table below, with algorithms for the operations versus the representations.

We combine the best of each representation by converting between coefficients and samples in O(n log n) time.

How? Consider the polynomial in matrix form.

where V is the Vandermonde matrix with entries vjk = xj^k .

Then we can convert between coefficients and samples using the matrix-vector product V · A, which is equivalent to evaluation. This takes O(n2). 

Similarly, we can samples to coefficients by solving V \Y (in MATLAB®notation). This takes O(n3) via Gaussian elimination, or O(n2) to compute A = V −1 · Y if V −1 is precomputed.

To do better than Θ(n2) when converting between coefficients and samples, and vice versa, we need to choose special values for x0, x1,...,xn−1. Thus far, we have only made the assumption that the xi values are distinct.

Divide and Conquer Algorithm

We can formulate polynomial multiplication as a divide and conquer algorithm with the following steps for a polynomial A(x) ∀ x ∈ X.

1.  Divide the polynomial A into its even and odd coefficients:
2. Recursively conquer Aeven(y) for y ∈ X2 and Aodd(y) for y ∈ X2, where X2 = {x2 | x ∈ X}.
3. Combine the terms. A(x) = Aeven(x2) + x · Aodd(x2) for x ∈ X.

We can do better if X is collapsing: either |X| = 1 (base case), or |X2| = |X| and 2 X2 is (recursively) collapsing

Roots of Unity

Collapsing sets can be constructed via square roots. Each of the following collapsing sets is computing by taking all square roots of the previous set.

FFT

We can take advantage of the nth roots of unity to improve the runtime of our polynomial multiplication algorithm. The basis for the algorithm is called the Discrete Fourier Transform (DFT).

The DFT allows the transformation between coefficients and samples, computing A → A∗ = V · A for xk = eiτ k/n where n = 2£ , where A is the set of coefficients and A∗ ∗ n−1 iτ jk/n is the resulting samples.

Fast Polynomial Multiplication

In order to compute the product of two polynomials A and B, we can perform the following steps.

1. Compute A∗ = FFT(A) and B∗ = FFT(B), which converts both A and B from coefficient vectors to a sample representation.
2. Compute C∗ = A∗ · B∗ in sample representation in linear time by calculating C∗ = A∗ · B∗ (∀k).
3. Compute C = IFFT(C∗), which is a vector representation of our final solution.