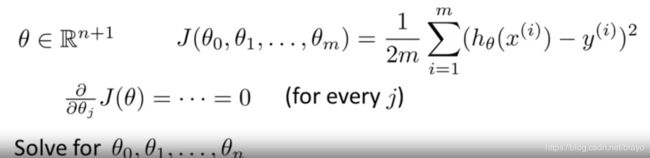第2周学习笔记-Coursera机器学习-吴恩达
文章目录
- Environment Setup Instructions
- Multivariate Linear Regression多元线性回归
- Multiple Features
- Gradient Descent for Multiple Variables
- Gradient Descent in Practice I - Feature Scaling(特征缩放)
- Gradient Descent in Practice II - Learning Rate
- Features and Polynomial(多项式) Regression
- Computing Parameters Analytically
- Normal Equation(正规方程)
- Normal Equation Noninvertibility(不可逆性)
- Submitting Programming Assignments
- Working on and Submitting Programming Assignments
- Subject: Confused about "h(x) = theta' * x" vs. "h(x) = X * theta?"
- Subject: Tips from the Mentors: submit problems and fixing program errors
- The Most Important Tip
- Running your scripts
- Making the grader happy
- Getting Help
- Debugging
- Unit Tests:
- Having trouble submitting your work to the grade?
- Octave/Matlab Tutorial
- Basic Operations
- Moving Data Around
- Computing on Data
- Plotting Data
- Control Statements: for, while, if statement
- Vectorization(向量化)
Environment Setup Instructions
octave是完全免费的(并且是开源的),而Matlab是商业软件,价格很昂贵(当然,这在当前国情下不是问题)。商业版的优势是有非常完善的服务,即使没有购买正版,也可以在MathWorks官方网站上获得很多非常有价值的资源。
Octave最初便是模彷Matlab而设计,语法基本上与Matlab一致,严谨编写的代码应同时可在Matlab及Octave运行,但也有很多细节上差别。一些软件开发小组也使用两者兼容的语法,直接开发可以同时在Matlab和Octave使用的程序。
本课程有三种方式编写程序:
- online Matlab
- matlab客户端
- Octave(强力推荐):因为吴老师后面课程视频基于Octave,而且Octave比matlab要轻量不少,总之免费简单好用。
Multivariate Linear Regression多元线性回归
Multiple Features
之前我们提到的 h θ ( x ) = θ 0 + θ 1 x h_{\theta }(x) = \theta_{0} + \theta_{1} x hθ(x)=θ0+θ1x,现在如果有多个变量见下图:
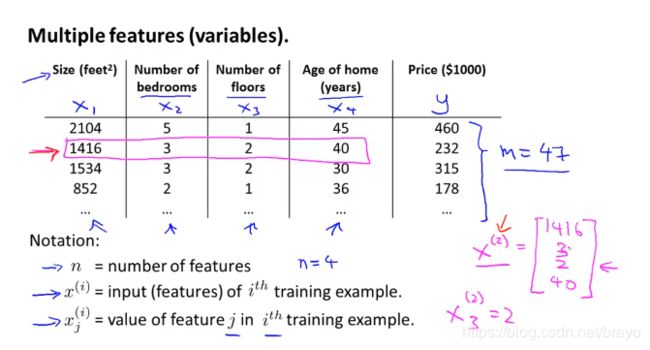
m:训练样本的个数
我们的假设函数就变为:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 h_{\theta }(x) = \theta_{0} + \theta_{1} x_1 + \theta_{2} x_2 + \theta_{3} x_3 + \theta_{4} x_4 hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4
上个式子的变量为4,现在拓展到n:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋅ ⋅ ⋅ + θ n x n h_{\theta }(x) = \theta_{0} + \theta_{1} x_1 + \theta_{2} x_2 + ···+ \theta_{n} x_n hθ(x)=θ0+θ1x1+θ2x2+⋅⋅⋅+θnxn
我们从 向量的角度 来表示上面式子:
为了方便起见,我们定义 x 0 = 1 ( 即 x 0 ( i ) = 1 ) x_{0}=1(即 x_{0}^{(i)} = 1) x0=1(即x0(i)=1).
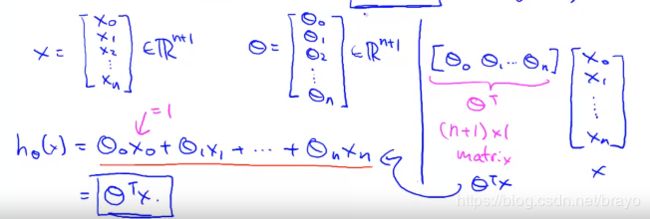
h θ ( x ) = [ θ 0 θ 1 . . . θ n ] [ x 0 x 1 . . . x n ] = θ T x h_{\theta}(x) = \begin{bmatrix} \theta_0 & \theta_1 & ... & \theta_n \end{bmatrix}\begin{bmatrix} x_0 \\ x_1 \\ ... \\ x_n \end{bmatrix} = \theta^{T}x hθ(x)=[θ0θ1...θn]⎣⎢⎢⎡x0x1...xn⎦⎥⎥⎤=θTx
注意 θ T \theta^{T} θT是1x(n+1)的矩阵,以上公式就是多元线性回归,多元指的是预测多个特征量或者变量。
Gradient Descent for Multiple Variables
左边是线性回归中的梯度下降算法,右边是多元线性回归中的梯度下降算法。两个算法的本质是一样的。

换句话说:
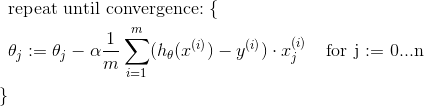
Gradient Descent in Practice I - Feature Scaling(特征缩放)
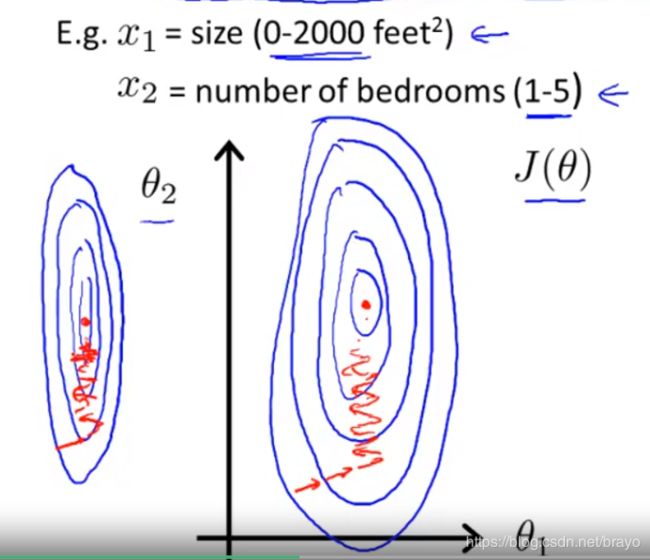
x 1 x_{1} x1 要比 x 2 x_{2} x2大很多,代价函数在图中是一个又瘦又高的圆。梯度下降很缓慢,花费很长时间,可能来回摆动,最终找到最小值的路。
改进:
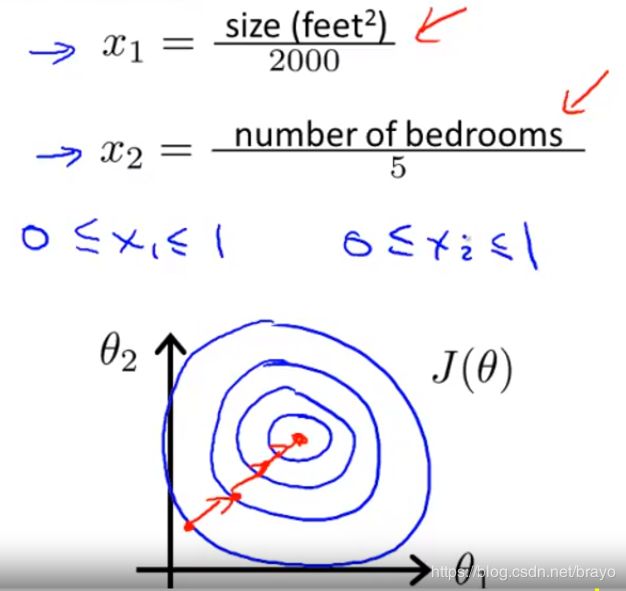
这样得到的代价函数偏移不会这么严重,更快地收敛,更容易找到通向最小值的捷径。
我们可以通过使每个输入值在大致相同的范围内来加速梯度下降。这是因为θ将在小范围内快速下降并且在大范围内缓慢下降,因此当变量非常不均匀时,将无效地振荡到最佳值。防止这种情况的方法是修改输入变量的范围,使它们大致相同。理想的情况是:
− 1 ≤ x ( i ) ≤ 1 -1\leq x_{(i)} \leq 1 −1≤x(i)≤1 或者 − 0.5 ≤ x ( i ) ≤ 0.5 -0.5\leq x_{(i)} \leq 0.5 −0.5≤x(i)≤0.5
这些并不是确切的要求。我们只是想加快速度。目标是将所有输入变量大致分为这些范围中的一个,给出或取一些。注意特征值太大和太小都不合适。

有两种帮助的技术是特征缩放和均值归一化。
- 特征缩放 涉及将输入值除以输入变量的范围(即最大值减去最小值),从而产生的新范围在1之内。
- 均值归一化 涉及从该输入变量的值中减去输入变量的平均值,从而导致输入变量的新平均值为0。
要实现这两种技术,调整输入值,如下面的公式所示:
x i : = x i − μ i s i x_{i}:=\frac{x_{i} - \mu_{i}}{s_{i}} xi:=sixi−μi
其中, μ i \mu_{i} μi 是所有特征值的平均值, s i s_{i} si 是值的范围(max - min)或者是标准差。
请注意,除以范围或除以标准偏差,会得到不同的结果。本课程中的测验使用范围 - 编程练习使用标准偏差。
特征缩放如何加速梯度下降?
通过避免在一个或多个特征(比其余特征具有更大的值)所需的许多额外迭代,来加速梯度下降。
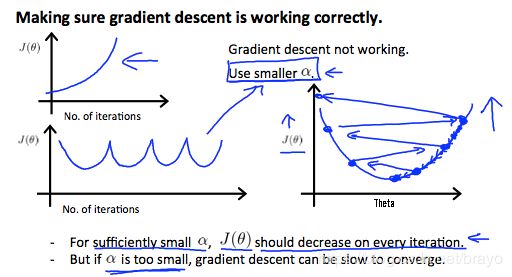
Gradient Descent in Practice II - Learning Rate
调试梯度下降:
-
一种是自动收敛测试。如果 J ( θ ) J(\theta) J(θ) 在一次迭代中减小于 E,则声明收敛,其中 E 是一些小的值,例如 $ 10^{-3}$。缺点是:在实践中很难选择这个阈值。
-
另一种比较直观的方式是在x轴上表示迭代次数,绘制成本函数 J ( θ ) J(\theta) J(θ) 随着梯度下降的迭代次数变化的图。如果 J ( θ ) J(\theta) J(θ) 增加,那么你可能需要减少 α 。

已经证明,如果学习率α足够小,那么 J ( θ ) J(\theta) J(θ) 将在每次迭代时减小。
学习率 α \alpha α 对 J ( θ ) J(\theta) J(θ)的影响:
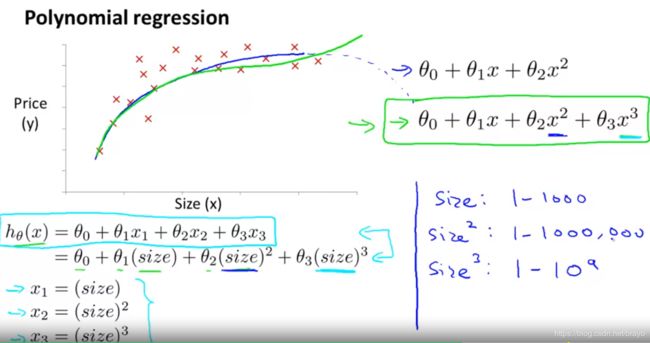
Features and Polynomial(多项式) Regression
我们可以通过几种不同的方式改进我们的特征和假设函数的形式。
- 我们可以将多个功能合二为一。例如:我们可以组合 x 1 x_{1} x1 和 x 2 x_{2} x2 变成新特征 x 3 = x 1 ⋅ x 2 x_{3} = x_{1} · x_{2} x3=x1⋅x2
- 我们的假设函数不必一定是直线,也可以是二次,三次或平方根函数(或任何其他形式)
-
上面部分采取两种拟合方式,一种是二次多项式函数拟合,但二次函数具有对称性,也就是后面会下降,效果不好;另一种是三次多项式函数,效果要更好。
-
左下部是多项式回归,其本质是多元线性回归。
-
右下部是多项式回归中,更应该 注意特征缩放问题。
-
我们的拟合函数还可以是其他类型,比如平方根函数:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 1 h_{\theta}(x) = \theta_{0} + \theta_{1}x_1 + \theta_{2}\sqrt{x_{1}} hθ(x)=θ0+θ1x1+θ2x1
Computing Parameters Analytically
Normal Equation(正规方程)
梯度下降给出了一种最小化代价函数 J J J 的方法。让我们讨论第二种方法,这次是明确地执行最小化代价函数而不是求助于迭代算法。这种方式叫正规方程。在“正规方程”方法中,我们将通过对 θ j \theta_{j} θj 求导并设置其导数为0 ,对代价函数 J J J 最小化。这允许我们在没有迭代的情况下找到最佳 θ \theta θ 。
正规方程不需要进行特征缩放
以下是梯度下降与正规方程的比较:
| Gradient Descent | Normal Equation |
|---|---|
| 需要选择学习率 α \alpha α | 不需要选择学习率 α \alpha α |
| 需要很多迭代 | 不需要迭代 |
| O ( k n 2 ) O(k n^{2}) O(kn2) | O ( n 3 ) O( n^{3}) O(n3) ,需要计算 ( X T X ) − 1 (X^{T} X)^{-1} (XTX)−1 |
| 当n很大时,效果好 | 当n很大时,运算慢 |
如果我们有非常多的特征,那么正规方程将会很慢。实际上,当n超过10,000时,可能是从正规方程转向迭代过程的好时机。
Normal Equation Noninvertibility(不可逆性)
在Octave中,我们想要使用正规方程,我们应该用 prin 函数而不是 inv 函数。prin 函数会计算 $ \theta$ 的值,即使$ X^{T}X$ 是不可逆的。注:singular matrix奇异矩阵/degenerate退化
X T X X^{T}X XTX 不可逆,常见的原因:
- Redundant features(冗余特征),其中两个特征密切相关(即它们是线性依赖的)。解决方法:删除与另一个线性相关的特征。
- 太多特征(e.g. m ≤ n)。在这种情况下,删除一些特征或使用“正规化”(将在后面的课程中解释)
Submitting Programming Assignments
Working on and Submitting Programming Assignments
Subject: Confused about “h(x) = theta’ * x” vs. “h(x) = X * theta?”
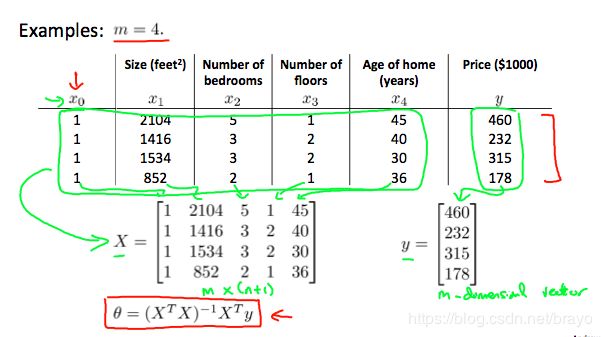
视频(和PDF文件)被组织为一次处理一个训练示例。该课程使用列向量(在大多数情况下),因此h(一个训练示例的标量)是theta’* x,即 h(x) = theta’ * x。
小写 x 通常表示单个训练示例。更有效的矢量化技术总是使用 X 作为所有训练示例的矩阵,每个示例作为一行,特征作为列。这样使得 X 的维度是 mxn(m是训练样本的个数).这样我们得到 h(x) = X * theta ,维度为(mx1)。
X(作为所有训练示例的矩阵)表示为大写 X 。
Subject: Tips from the Mentors: submit problems and fixing program errors
The Most Important Tip
在发布新问题之前搜索论坛。如果您有问题,可能是其他人已经发布了该问题,并收到了答案。通过在发布新主题之前搜索主题,为自己和论坛用户节省时间。
Running your scripts
在Octave/Matlab的命令行,你不需要包含脚本文件名的“.m”部分。因此,通过在命令行输入“ex1”来运行Exercise 1脚本。
使用提交脚本时,您也不需要包括括号(),只需要输入"submit".
只输入函数的名称无法执行函数的功能。你将要处理的所有函数都需要一组参数值,在一组括号之间输入。你测试代码的三种方法:
-
使用exercise脚本,比如"ex1"
-
使用单元测试(见下文),您可以在其中输入包括参数在内的整个命令行
-
使用submit脚本
Making the grader happy
你的函数必须处理一般情况,这意味着:
- 您应该避免使用硬编码的数组索引。
- 你应该避免使用固定长度的数组和矩阵。
学生们认为获得PDF文件中列出的相同答案意味着他们应该从评分者那里获得全部学分是很常见的。这是一个错误的希望。 PDF文件只是一个测试用例。评分者使用不同的测试用例。此外,评分者不喜欢您的代码将任何其他输出发送到工作区。因此,每行代码都应以分号结尾。
Getting Help
如果您需要论坛社区的帮助,请使用此两步程序:
-
在论坛中搜索与您的问题相关的关键字。按功能名称搜索是一个好的开始。
-
如果找不到合适的线索,请执行以下操作:
2a. 找到该练习的单元测试(见下文),并运行相应的测试。尝试调试代码
2b. 获取整个控制台工作区(包括命令行)的屏幕截图,并将其发布到论坛,以及任何其他有用信息(计算机类型,Octave / Matlab版本,您尝试过的其他测试等)。
Debugging
如果您的代码运行但给出了错误的答案,您可以在函数结束前在脚本中插入 “keyboard” 命令。这将导致程序退出到调试器,因此您可以从命令行检查所有变量。这通常非常有助于分析数学错误,或尝试使用哪些命令来实现您的功能。
“All Course Discussions”下的固定thread中列出了其他测试用例和教程。测试用例特别有助于在ex中获得预期输出但在提交时没有得分或出错的情况下进行调试。
Unit Tests:
每个编程任务在论坛中都有一个“Discussions”区域。在本节中,您经常可以找到“单元测试”。这些是附加测试用例,它们为您提供键入命令,并提供预期结果。在提交给评分者之前,使用单元测试来测试您的功能总是一个好主意。
如果您运行单元测试并且没有获得正确的结果,您可以通过发布工作区的屏幕截图(包括您输入的命令行和结果)轻松获得论坛的帮助。
Having trouble submitting your work to the grade?
- 如果您运行提交脚本并收到无法验证您的身份的消息,请确保您已使用Coursera帐户电子邮件和编程分配提交密码登录。
- 如果收到“提交未定义”消息,请首先检查您是否在从ZIP存档中解压缩文件的工作目录中。如有必要,请使用“cd”到达那里。
- 如果“submit undefined”错误仍然存在,或者出现任何其他“函数未定义”消息,请尝试使用“addpath(pwd)”命令将当前工作目录(pwd)添加到Octave执行路径。
- 如果提交脚本崩溃并显示错误消息,请参阅“All Course Discussions”下的“Mentor tips for submitting your work”主题。
- 提交脚本不会询问您要提交的练习的哪个部分。它会自动为您修改的任何功能评分。
Octave/Matlab Tutorial
Basic Operations
建议使用Octave
加减乘除没有特别操作。
% 基础操作和变量赋值
== % 是否等于
~= % 是否不等于
&& % AND
|| % OR
xor(1,0) % 异或运算,返回1
% 修改命令行前面形式:>> ...
PS1('>> ');
a = 3 %直接给变量赋值
a = 3; % 给变量赋值3,并且不在命令行显示
b = 'hi' % 字符串变量赋值
c = (3>=1); % c=1
% 以下a复制后没有改变
a = pi
a % 打印出:a = 3.1416
disp(a) % 打印出:a = 3.1416
disp(sprintf('2 decimals:%0.2f', a)) % 打印出:2 decimals:3.14
format long
a % 打印出:a = 3.141592653589793
format short
a % 打印出:a = 3.1416
% 向量和矩阵
A = [1 2;3 4;5 6] % A是3行2列矩阵,分号作用是矩阵内换行。
v = [1 2 3] % v是1行3列的向量
v = [1; 2; 3] % v是3行1列的向量
v = 1:0.1:2 % v是一个行向量,第一列为1,依次以步长0.1增长到2.
v = 1:6 % v是一个行向量,第一列为1,依次以步长1增长到6.
ones(2,3) % 生成2x3矩阵,矩阵每个元素是1
c = 2*one(2,3) % c是2x3矩阵,矩阵每个元素是2
w = zeros(1,3) % 类似的w是 1x3 的0矩阵
w = rand(3,3) % 矩阵的所有值服从[0,1]分布(uniform distribution)
w = randn(1,3) % 矩阵的所有值服从均值为0,方差为1的正态分布(normal distribution),注意加分号
w = -6 + sqrt(10)*(randn(1,10000)) % w
hist(w) % 根据w,绘制一个10个方块直方图:类似正太分布,(均值 = -6, 方差 = 10)
hist(w,50) % 绘制50方块的直方图
eye(4) % 生成一个4阶的单位矩阵
% help 帮助
help eye % 显示eye函数的帮助文档,按q退出
help rand % 显示rand函数的帮助文档,按q退出
help help
Moving Data Around
对于一个机器学习问题,如何把数据加载到Octave中?如何把数据存入矩阵,进行运算?如何保存计算结果?本节解决这些问题。
% 维数显示
A = [1 2;3 4;5 6]
size(A) % 返回1x2矩阵:3 2
size(A,1) % 返回A矩阵第一个维度尺寸:3
length(A) % 返回A维度最大的值:3
% 目录操作
pwd % 显示Octave当前所处路径
cd 'F:\MLwork' % 进入到输入目目中
ls % 显示当前目录的所有文件
% 读写数据
% 假设我们进入到目录,当前目录中有2个文件:featuresX.dat 特征向量文件;priceY.dat 标签文件
load featuresX.dat % 加载featuresX.dat文件
load ('featuresX.dat') % 加载featuresX.dat文件
load priceY.dat % 加载priceY.dat文件
who % 显示当前Octave存储的所有变量
% 之前加载了featuresX.dat文件,其数据存在变量featuresX
whos % 显示当前Octave存储的所有变量的详细信息
% featuresX size(47x2); priceY size(47x1)
clear featuresX % 清除了变量featuresX,再输入whos,发现featuresX没有了
clear % 清除工作空间中所有变量
v = priceY(1:10) % 将向量priceY前10个数赋给v,v size(10x1)
save hello.mat v; % 将向量v以二进制形式存入hello.mat文件中,没有会创建该文件
save hello.txt v -ascii % 以ASCII形式保存到txt文件中
% 矩阵索引
A = [1 2;3 4;5 6]
A(3,2) % 表示A的第3行第2列元素:6
A(2,:) % ":"表示该行或该列的所有元素:3 4
A([1 3],:) % 返回第1行和第3行的所有元素
A(:,2) = [10; 11; 12] % 把第2列元素替换成[10; 11; 12]
A = [A, [100; 101; 102]]; % 再原来矩阵的右边增加一个列矩阵[100; 101; 102]. size(3x3)
A(:) % 特殊语法:把所有A中元素放入到一个列向量中.size(9x1)
% 矩阵组合
A = [1 2; 3 4; 5 6];
B = [11 12; 13 14; 15 16];
C = [A B]
C = [A, B] % 两个C等价
%{
C =
1 2 11 12
3 4 13 14
5 6 15 16
%}
C = [A; B] % ";"把B放在A的下面
%{
C =
1 2
3 4
5 6
11 12
13 14
15 16
%}
Computing on Data
A = [1 2; 3 4; 5 6]
B = [11 12; 13 14; 15 16]
C = [1 1; 2 2]
A*C % A与C矩阵相乘
A .* B % A的每个元素乘以B对应的元素
%{
ans =
11=1x11 24=2x12
39=3x13 56=4x14
75=5x15 96=6x16
%}
A .^ 2 % A自身元素平方
%{
ans =
1 4
9 16
25 36
%}
v = [1; 2; 3]
1 ./ v % V中元素= 1 / 元素
%{
ans =
1.00000
0.50000
0.33333
%}
% 类似的只是根据v中元素进行操作
log(v) % 取对数
exp(v) % e^{..}
abs(v) % 取绝对值
-v % 取负:-1*v
v = [1; 2; 3]
v + ones(leng(v), 1) % v每项+1
v + 1 % v每项+1
A = [1 2; 3 4; 5 6]
A' % A的转置矩阵
a = [1 15 2 0.5]
val = max(a) % val = 15
[val, ind] = max(a)
%{
val = 15
ind = 2
%}
max(A) % max(x):如果x是矩阵,则默认返回每列的最大值
%{
ans =
5 6
%}
a < 3 % a的元素跟3相比
%{
ans =
1 0 1 1
%}
find(a < 3) % 找到符合条件元素下标
%{
ans =
1 3 4
%}
A = magic(3) % 创建3阶矩阵,每行每列的和相同
%{
A =
8 1 6
3 5 7
4 9 2
%}
[r,c] = find(A >= 7) % 类似向量的find
%{
r =
1
3
2
c =
1
2
3
%}
a = [1 15 2 0.5]
sum(a) % a中所有元素求和
prod(a) % a中所有元素求积
floor(a) % a中所有元素向下取整
ceil(a) % a中所有元素向上取整
max(rand(3), rand(3)) % 两个随机生成矩阵取最大元素生成3阶矩阵
%{
A =
8 1 6
3 5 7
4 9 2
%}
max(A, [], 1) % 每列取最大
%{
ans =
8 9 7
%}
max(A, [], 2) % 每行取最大
%{
ans =
8
7
9
%}
max(max(A)) % 返回A中的最大值
max(A(:)) % 返回A中的最大值
sum(A,1) % A的每列求和
%{
ans =
15 15 15
%}
sum(A,2) % A的每行求和
%{
ans =
15
15
15
%}
sum(sum(A.*eye(3))) % 求主对角线元素之和:ans = 15
sum(sum(A.*flipud(eye(3))) % 求副对角线元素之和
flipud(eye(3))
%{
0 0 1
0 1 0
1 0 0
%}
pinv(A) % A的逆矩阵
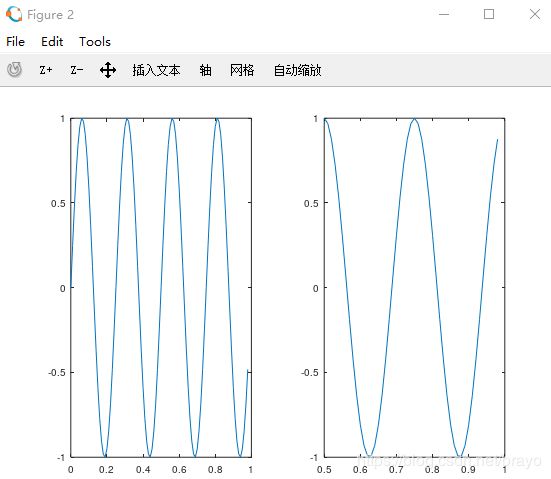
Plotting Data
t = [0:0.01:0.98]
y1 = sin(2*pi*4*t);
plot(t, y1); % x轴是t, y轴是y1
y2 = cos(2*pi*4*t);
plot(t, y2) ;% 消除原来的正弦函数,绘制余弦函数
% 同时显示正弦函数和余弦函数
plot(t, y1);
hold on;
plot(t, y2, 'r'); % 在原图上用红线画余弦函数
xlabel('time') % 设置x轴名称
ylabel('value') % 设置y轴名称
legend('sin','cos') % 对函数线标记
title('my plot') % 设置图标题
cd 'F:\MLwork' % 进入到目录中
print -dpng 'myplot.png' % 保存为png
close % 关闭图像
figure(1); plot(t, y1); % 以figure1窗口打开图像
figure(2); plot(t, y2); % 以figure2窗口打开图像,上面2者同时打开
% 此时我们打开figure2窗口
subplot(1,2,1); % 将figure2分为1x2格子,现在使用第1格
plot(t, y1);
subplot(1,2,2);% 将figure2分为1x2格子,现在使用第2格
plot(t, y2);
axis([0.5 1 -1 1]) % 设置右边的图x轴范围0.5到1,y轴范围-1到1
clf; % 清除图
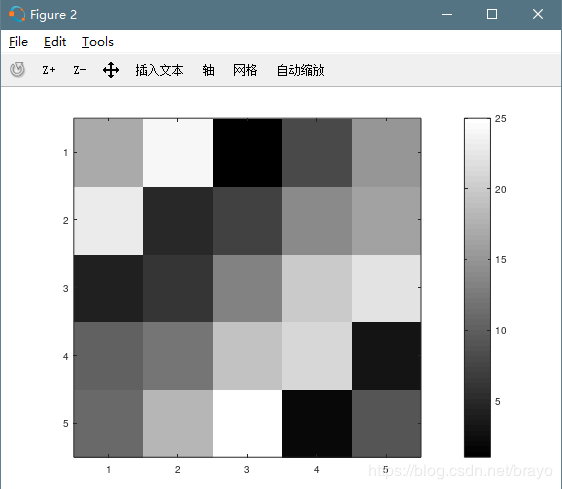
% 矩阵可视化
A = magic(5)
imagesc(A) % A的元素值不同,对应不同颜色
imagesc(A), colorbar, colormap gray; % 同时运行三个命令。逗号连接函数使得命令同时执行。如果是分号,则不显示结果。
Control Statements: for, while, if statement
v = zeros(10,1);
% 1和2结果一样
for i=1:10,
v(i) = 2^i;
end;
% 2
indices=1:10
%{
indices =
1 2 3 4 5 6 7 8 9 10
%}
for i=indices,
disp(i);
end;
i = 1;
while i<= 5,
v(i) = 100;
i = i+1;
end;
i = 1;
while true,
v(i) = 999;
i = i+1;
if i==6,
break;
end;
end;
v(1) = 2;
if v(1) == 1,
disp('The value is one');
elseif v(1) == 2,
disp('The value is two');
else
disp('The value is not one or two');
end; % end一定不要忘记
% 函数可以写在文件中,Octave找到对应路径(Octave所在路径和你的文件路径一致),输入函数名和参数就可以运行函数。
% 添加Octave搜索路径,当Octave进入到其他目录,也会知道你添加的路径中的文件。
addpath('F:\test')
% 函数返回一个值(写在文件中)
function y = squareThisNumber(x)
y = x^2;
% 函数返回多个值(写在另一文件中)
function [y1, y2] = squareandCubeThisNumber(x)
y1 = x^2;
y2 = x^3;
% 命令行输入
[a,b] = squareandCubeThisNumber(5)
Vectorization(向量化)
说明:
- 左下部是未使用向量化方法,直接使用for;
- 右下部使用向量化的方法。
说明:
- 这里使用向量化方法。
- 右上部只是举个例子,说明同时更新 v(j) 和 w(j) 可以采用向量化方法。