2D Image Morphing Algorithms
2D Image Morphing Algorithms
1. 2 Published Algorithms for Warping
- Mesh warping
- Feature-Based (Field) morphing
2. Mesh Warping[1]
The mesh-warping algorithm relates features with nonuniform mesh in thesource and destination images, i.e., the images are broken up intosmall regions that are mapped onto each other for the morph.The algorithm accepts a source image, a destination image and two2D arrays of coordinates. The first array, S, specifies the coordinatesof control points in the source image. The second array, D, specifies theircorresponding positions in the destination image. Both S and D must havethe same dimensions in order to establish a one-to-one correspondence.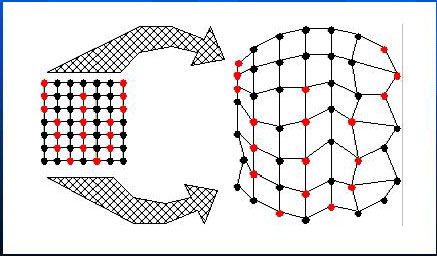
Source Image |
 Destination Imge |
Figure2 Original Images for morphing
|
|
 |
Then two imges are processed through 2-pass warping with 2 output intermediateimages I1 and I2. The first pass is responsible for resampling each rowindependently. It maps all initial image points coordinates (u, v) to their(x, v) coordinates in the intermediate image , thereby positioning eachinput point into its proper output column.The second pass then resampleseach column in intermediate image, mapping every (x, v) point to its final(x, y) position in I1/I2. The 2D arrays in which the control points arestored to impose a topology to the mesh.
More detail is that each frame in the transformation uses an interpolatedmesh M as the set of target positions for the input mesh points. M is computedby performing linear interpolation between respective points in S and D.The "warp" program actually plays an important role here since both I1and I2 are each warped using M as the target mesh. Thus, I1 is warped usingmeshes S and M. In addition, I2 is warped using meshes D and M. Now thatthe landmarks of the source and target images are aligned, they are cross-dissolvedto generate a morph frame. Catmull-Rom cubic spline is used to implementbicubic interpolation in [3] because it offers local control, althoughany spline wourld suffice.
Result:
Source code for Mesh-morphing: (Some changes are made to the image morphingsource codes written by George Wolberg in order to morphing the color images.)
1. Transform a RGB format file to three BW format files in term ofdifferent color channel [code]
2. Morphing Source Code (written by George Wolberg,1993.) [see detailat http://www.engr.ccny.cuny.edu/CSCWWW/faculty/wolberg/abstracts.html#cga97]
Makefile: dependency rules for creating "warp" and "morph"3. Merging three channel's BW format images into one RGB color image [code]
meshwarp.h header file
warp.c: main function for "warp"
morph.c: main function for "morph"
meshwarp.c: workhorse mesh warping code
util.c: image I/O and memory allocation functions
catmullrom.c: Catmull-Rom cubic spline interpolation.
Pros and Cons:
|
|
|
|
|
3. Feature-Based Image Morphing [2]
The field morphing algorithm uses lines to relate features in the sourceimage to features in the destination image. It is based upon fields ofinfluence surrounding two-dimensional control primitives. It applies thereverse mapping as its ways of warping.[ Note: There are 2 ways to warp an image. The first,called forward mapping, scans through the source image pixel by pixel,and copies them to teh apprpriate place in the destination image. The second,reverse mapping, goes through the destination image pixel by pixel, andsamples the correct pixel from the source image. The most important featureof inverse mapping is that every pixel in the destination image gets setto something appropriate. In the forward mapping case, some pixels in thedestination might not get painted, and would have to be interpolated.]
Transformation between one pair of lines
A pair of lines (one defined relative to the source image, the other definedrelative to the destination image) defines a mapping from one image tothe other. where u is the position along the line, and v is the distance fromthe line |
 |
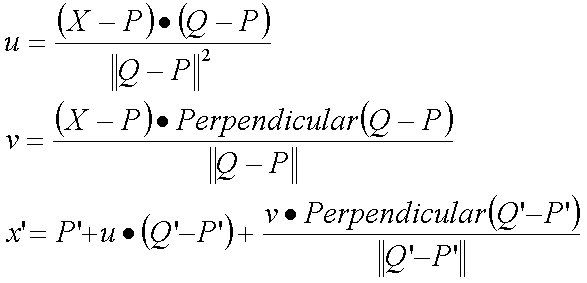The algorithms transforms each pixel coordinate by a rotation, translation,and/or a scale, thereby transforming the whole image.
Transformation between multiple pairs of lines
Normally there are many features in images where transformation betweenmultiple pairs of lines are applied. It specifies more complex transformations.A weighting of the coordinate transformations for each line is performed.The weight is determined by the distance from X to the line.
 |
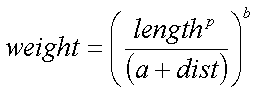where length is the length of a line, dist is the distance from thepixel to the line, and a, b, and p are constants that can be used to changethe relative effect of the lines |
The multiple line algorithm is as follows:
For each pixel X in the destination
DSUM=0
weightsum = 0
For each line PiQi
calculate u, v based on PiQi
calculate X’i based on u, v and P’iQ’i
calculate displacement Di=X’i-Xi for this line
dist= shortest distance from X to PiQi
weight = (lengthP / (a + dist))b
DSUM += Di * weight
weightsum += weigth
X’ = X + DSUM / weightsum
destinationImage(X) = sourceImage(X’)
Process of Morphing between Two images
- Define corresponding lines in source image I0 and destination image I1.
- Each intermediate frame I of the metamorphosis is defined by creating anew set of line segments by interpolating the lines from their positionsin I0 to the positions in I1.
- Both images I0 and I1 are distorted toward the position of the lines inI. These two resulting images are cross-dissolved throughout the metamorphosis.
Example
 Source Image |
 Destination Image |
 |
Left figure is the first face distorted to the intermediate positionwithout the grid or lines. |
 |
Same as above figures with lines drawn over the faces. |
 |
Left figure is the second face distorted to the intermediate positionwithout the grid or lines. |
 |
Same as above figures with lines drawn over the faces. |
 |
Left figure shows the morphed image (right figure) with the interpolatedlines drawn over it. |
Advantage and disadvantage
|
|
|
| The only positions that are used in the algorithm are ones the animatorexplicitly created. Everything that is specified is moved exactly as theanimator wants them moved, and everything else is blended smoothly basedon those positions. |
|