NOI 2004 沙丘 dune
首先,由于已访问的每个点的度数都是已知的,可以通过记录从根到当前点的路径上每个点所走的弧的编号(设为cur_arc[path[i]],i为深度)来回到根结点(walk(degree[path[i]] - cur_arc[path[i]]))。
如果原图是一棵树,可以直接做,相当于模拟DFS。(因为树上DFS只要不走通往父节点的边,就不必判重)。
下面考虑如何判断环,并记录下相应的后向边:
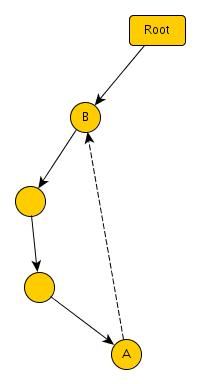
如图,DFS搜索树上,AB是后向边。如果现在已经在B放置了一个标记,那么从A向根走,会经过B。此时可以知道有一个环,但不知道在B上边BA的序号。因此从B拿到标记后退回A,在A处放标记,再回到B,枚举B的每一条出边,直到到达一个有标记的点,则此时枚到的边为BA。在此边做上不可访问的标记,并回到A。
因此,扩展每个点的时(例如从M走到N),先在新走到的点(N)上放上标记,在从原来的点(M)向根走,如果中途没遇到有标记的点,则说明N是未访问的点,回到N开始DFS;如果遇到一个有标记的点,则发现了环,标记相应的后向边后从M枚举N的下一个点。
另外还有一个问题,1号点的0号边是不确定的。我的解决办法是,先调用walk(0),再dfs,然后判断一下dfs所得的root的0号边是否被标记为不可访问,如果不是,就调用walk(0)并再次dfs。
实现中很多细节非常纠结,还好数据比较厚道,构造出来就给了10分。
/* * $File: dune.cpp * $Date: Fri May 14 19:32:24 2010 +0800 */ #include "dune_lib.h" #include <cassert> namespace Solve { const int NVTX_MAX = 105; int nvtx, degree[NVTX_MAX], cur_arc[NVTX_MAX], path[NVTX_MAX], npath; bool arc_nouse[NVTX_MAX][NVTX_MAX]; bool check(); // before check(), sign should be on hand // after check(), we should stay at the same vertex, // and the sign should be on hand // // the status seems to be walking from root to the current vertex void dfs(); void solve(); } void Solve::solve() { init(); walk(0); dfs(); if (!arc_nouse[0][0]) dfs(); int m = 0; for (int i = 0; i < nvtx; i ++) m += degree[i]; report(nvtx, m >> 1); } void Solve::dfs() { int root = nvtx ++, d; bool sign; look(d, sign); if (sign) take_sign(); degree[root] = d; if (d == 1) { walk(0); return; } path[npath ++] = root; bool last_check = true; for (int i = 1; ; i ++) { int cnt = 1; while (i < d && arc_nouse[root][i]) i ++, cnt ++; cur_arc[root] = i; arc_nouse[root][i] = true; if (last_check) walk(cnt); else walk(i % d); if (i == d) { npath --; return; } put_sign(); if (npath == 1) { dfs(); last_check = true; } else { walk(0); last_check = check(); if (last_check) { walk(i); dfs(); } } } } bool Solve::check() { bool ret = true; int istart = 0; for (int i = npath - 1; i > 0; i --) { int curv = path[i]; walk(degree[curv] - cur_arc[curv]); int d; bool sign; look(d, sign); if (sign) { take_sign(); walk(0); for (int j = i; j + 1 < npath; j ++) walk(cur_arc[path[j]]); put_sign(); walk(0); for (int j = npath - 2; j >= i; j --) walk(degree[path[j]] - cur_arc[path[j]]); int cnt = 0; while (1) { walk(1); look(d, sign); if (sign) take_sign(); walk(0); cnt ++; if (sign) break; } int v1 = path[i - 1], tmp = cur_arc[v1] + cnt; if (tmp == degree[v1]) tmp = 0; assert(tmp < degree[v1]); arc_nouse[v1][tmp] = true; ret = false; walk(degree[v1] - cnt); istart = i; break; } } if (!istart) { istart = 1; walk(0); } for (int i = istart; i + 1 < npath; i ++) walk(cur_arc[path[i]]); return ret; } int main() { Solve::solve(); }
Problem: dune
Point Execution Status Score Time [sec] Memory [kb]
1 Normal 10.000 0.007 2360
2 Normal 10.000 0.060 3212
3 Normal 10.000 0.006 2364
4 Normal 10.000 0.007 2412
5 Normal 10.000 0.006 2488
6 Normal 10.000 0.007 2412
7 Normal 10.000 0.008 2652
8 Normal 10.000 0.008 2660
9 Normal 10.000 0.016 2840
10 Normal 10.000 0.025 3180