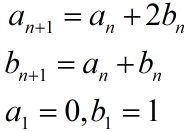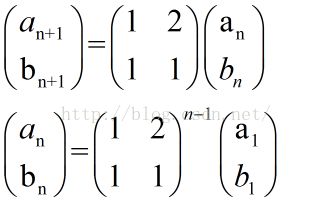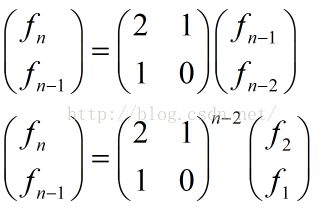矩阵快速幂的应用(郭姐散步)

题目：

http://nucacm.openjudge.cn/practice/00001/

http://nucacm.openjudge.cn/practice/00013/(升级版)

题意:

GJ散步，最开始在坐标系的中心（0,0），他可以向上，向左，向右但是不能向下，给出n表示GJ走的步数，对于小数据(第一题)n <= 1000000，对于大数据(第二题)n <= 1e18，求公有多少种走的方法？

题解：

常见的一种矩阵快速幂的应用。

由分析可知，每一步的下一步可以有两种或者三种选择，有两种选择的步其下一步的选择数为2+3，有三种选择的步其下一步为2+2+3.

所以设a_n为2的个数，b_n 为3的个数，ans即为2*a_n+3*b_n 

又有

所以

接下来就可以用矩阵快速幂来求解。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2;
const int MOD=1e9+7;
typedef long long LL;
struct Matrix
{
	LL m[N][N];
	Matrix(){};
	Matrix unit()
	{
		for(int i=0;i<N;i++)
		{
			for(int j=0;j<N;j++)
			{
				m[i][j]=i==j?1:0;
			}
		}
	}
	void print()
	{
		for(int i=0;i<N;i++)
		{
			for(int j=0;j<N;j++)
			{
				printf("%lld ",m[i][j]);
			}
			printf("\n");
		}
	}
};
Matrix operator *(Matrix a,Matrix b)
{
	Matrix c;
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			c.m[i][j]=0;
			for(int k=0;k<N;k++)
			{
				c.m[i][j]=(c.m[i][j]+((a.m[i][k]%MOD)*(b.m[k][j]%MOD))%MOD)%MOD;
			}
		}
	}
	return c;
}
Matrix operator ^(Matrix a,LL k)
{
	Matrix c;
	c.unit();
	while(k)
	{
		if(k&1) c=c*a;
		k>>=1;
		a=a*a;
	}
	return c;
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	Matrix a;
	a.m[0][0]=1;
	a.m[0][1]=2;
	a.m[1][0]=1;
	a.m[1][1]=1;
//	a.print();
/*	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			printf("%lld ",a.m[i][j]);
		}
		printf("\n");
	}*/
	int T;
	scanf("%d",&T);
	while(T--)
	{
		LL n;
		scanf("%lld",&n);
		//cin>>n;
		if(n<=0) printf("0\n");
		else if(n==1) printf("3\n");
		else if(n==2) printf("7\n");
		else 
		{
			Matrix ans=a^(n-1);
			//ans.print();
			printf("%lld\n",((ans.m[0][1]*2%MOD)+(ans.m[1][1]*3%MOD))%MOD);
		}
	}
	return 0;
}</span>

如果设Fn为总的方案数，可以求出递推式

（怎么出来的我也忘了QAQ），则也可以有

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2;
const int MOD=1e9+7;
typedef long long LL;
struct Matrix
{
	LL m[N][N];
	Matrix(){};
	Matrix unit()
	{
		for(int i=0;i<N;i++)
		{
			for(int j=0;j<N;j++)
			{
				m[i][j]=i==j?1:0;
			}
		}
	}
	void print()
	{
		for(int i=0;i<N;i++)
		{
			for(int j=0;j<N;j++)
			{
				printf("%lld ",m[i][j]);
			}
			printf("\n");
		}
	}
};
Matrix operator *(Matrix a,Matrix b)
{
	Matrix c;
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			c.m[i][j]=0;
			for(int k=0;k<N;k++)
			{
				c.m[i][j]=(c.m[i][j]+((a.m[i][k]%MOD)*(b.m[k][j]%MOD))%MOD)%MOD;
			}
		}
	}
	return c;
}
Matrix operator ^(Matrix a,LL k)
{
	Matrix c;
	c.unit();
	while(k)
	{
		if(k&1) c=c*a;
		k>>=1;
		a=a*a;
	}
	return c;
}
int main()
{
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	Matrix a;
	a.m[0][0]=2;
	a.m[0][1]=1;
	a.m[1][0]=1;
	a.m[1][1]=0;
//	a.print();
/*	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			printf("%lld ",a.m[i][j]);
		}
		printf("\n");
	}*/
	int T;
	scanf("%d",&T);
	while(T--)
	{
		LL n;
		scanf("%lld",&n);
		//cin>>n;
		if(n<=0) printf("0\n");
		else if(n==1) printf("3\n");
		else if(n==2) printf("7\n");
		else 
		{
			Matrix ans=a^(n-2);
			//ans.print();
			printf("%lld\n",((ans.m[0][0]*7%MOD)+(ans.m[0][1]*3%MOD))%MOD);
		}
	}
	return 0;
}</span>