0028算法笔记——【回溯法】批作业调度问题和符号三角形问题

  1、批作业调度问题

     (1)问题描述

     给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理，然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。

     批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

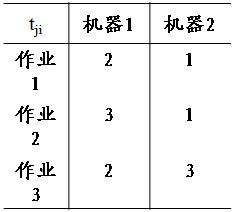
      例：设n=3，考虑以下实例：

     这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。

     (2)算法设计

     批处理作业调度问题要从n个作业的所有排列中找出具有最小完成时间和的作业调度，所以如图，批处理作业调度问题的解空间是一颗排列树。按照回溯法搜索排列树的算法框架，设开始时x=[1,2,……n]是所给的n个作业，则相应的排列树由x[1:n]的所有排列构成。

     算法具体代码如下：

#include "stdafx.h"
#include <iostream>
using namespace std;

class Flowshop
{
    friend int Flow(int **M,int n,int bestx[]);
    private:
        void Backtrack(int i);

        int **M,    // 各作业所需的处理时间
            *x,     // 当前作业调度
            *bestx,    // 当前最优作业调度

            *f2,    // 机器2完成处理时间
            f1,    // 机器1完成处理时间
            f,     // 完成时间和

            bestf,    // 当前最优值
            n;  // 作业数
 };

int Flow(int **M,int n,int bestx[]);

template <class Type>
inline void Swap(Type &a, Type &b);

int main()
{
    int n=3,bf;
    int M1[4][3]={{0,0,0},{0,2,1},{0,3,1},{0,2,3}};

    int **M=new int*[n+1];

    for(int i=0;i<=n;i++)
    {
        M[i]=new int[3];
    }
    cout<<"M(i,j)值如下："<<endl;

    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<3;j++)
        {
            M[i][j]=M1[i][j];
        }
    }

    int bestx[4];
    for(int i=1;i<=n;i++)
    {
        cout<<"(";
        for(int j=1;j<3;j++)
        cout<<M[i][j]<<" ";
        cout<<")";
    }

    bf=Flow(M,n,bestx);

    for(int i=0;i<=n;i++)
    {
        delete []M[i];
    }
    delete []M;

    M=0;

    cout<<endl<<"最优值是："<<bf<<endl;
    cout<<"最优调度是：";

    for(int i=1;i<=n;i++)
    {
        cout<<bestx[i]<<" ";
    }
    cout<<endl;
    return 0;
}

void Flowshop::Backtrack(int i)
{
    if (i>n)
    {
        for (int j=1; j<=n; j++)
        {
            bestx[j] = x[j];
        }
        bestf = f;
    }
   else
   {
        for (int j = i; j <= n; j++)
        {
            f1+=M[x[j]][1];
            //机器2执行的是机器1已完成的作业，所以是i-1
            f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2];

            f+=f2[i];
            if (f < bestf)//剪枝
            {
                Swap(x[i], x[j]);
                Backtrack(i+1);
                Swap(x[i], x[j]);
            }
            f1-=M[x[j]][1];
            f-=f2[i];
        }
    }
}

int Flow(int **M,int n,int bestx[])
{
    int ub=30000;

    Flowshop X;
    X.n=n;
    X.x=new int[n+1];
    X.f2=new int[n+1];

    X.M=M;
    X.bestx=bestx;
    X.bestf=ub;

    X.f1=0;
    X.f=0;

    for(int i=0;i<=n;i++)
    {
        X.f2[i]=0,X.x[i]=i;
    }
    X.Backtrack(1);
    delete []X.x;
    delete []X.f2;
    return X.bestf;
}

template <class Type>
inline void Swap(Type &a, Type &b)
{
    Type temp=a;
    a=b;
    b=temp;
}

#include "stdafx.h"
#include <iostream>
using namespace std; 

class Flowshop
{
	friend int Flow(int **M,int n,int bestx[]);
	private:
		void Backtrack(int i);

		int **M,    // 各作业所需的处理时间
			*x,     // 当前作业调度
			*bestx,    // 当前最优作业调度

			*f2,    // 机器2完成处理时间
			f1,    // 机器1完成处理时间
			f,     // 完成时间和

			bestf,    // 当前最优值
			n;  // 作业数
 }; 

int Flow(int **M,int n,int bestx[]);

template <class Type>
inline void Swap(Type &a, Type &b);

int main()
{
	int n=3,bf;
	int M1[4][3]={{0,0,0},{0,2,1},{0,3,1},{0,2,3}};

	int **M=new int*[n+1];

    for(int i=0;i<=n;i++)
	{
        M[i]=new int[3];
	}
	cout<<"M(i,j)值如下："<<endl;

	for(int i=0;i<=n;i++)
	{
		for(int j=0;j<3;j++)
		{
			M[i][j]=M1[i][j];
		}
	}

	int bestx[4];
    for(int i=1;i<=n;i++)
	{
		cout<<"(";
		for(int j=1;j<3;j++)
		cout<<M[i][j]<<" ";
		cout<<")";
	}

	bf=Flow(M,n,bestx);

	for(int i=0;i<=n;i++)
	{
		delete []M[i];
	}
    delete []M;

    M=0;

	cout<<endl<<"最优值是："<<bf<<endl;
	cout<<"最优调度是：";

	for(int i=1;i<=n;i++)
	{
		cout<<bestx[i]<<" ";
	}
	cout<<endl;
	return 0;
}

void Flowshop::Backtrack(int i)
{  
	if (i>n)
	{
		for (int j=1; j<=n; j++)
		{
			bestx[j] = x[j];
		}
		bestf = f;
	}
   else
   {
		for (int j = i; j <= n; j++)
		{
			f1+=M[x[j]][1];
			//机器2执行的是机器1已完成的作业，所以是i-1
			f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2];

			f+=f2[i];
			if (f < bestf)//剪枝
			{
				Swap(x[i], x[j]);
				Backtrack(i+1);
				Swap(x[i], x[j]);
			}
			f1-=M[x[j]][1];
			f-=f2[i];
		}
	}
}

int Flow(int **M,int n,int bestx[])
{
	int ub=30000;

	Flowshop X;
	X.n=n;
	X.x=new int[n+1];
	X.f2=new int[n+1];

	X.M=M;
	X.bestx=bestx;
	X.bestf=ub;

	X.f1=0;
	X.f=0;

	for(int i=0;i<=n;i++)
	{
		X.f2[i]=0,X.x[i]=i;
	}
	X.Backtrack(1);
	delete []X.x;
	delete []X.f2;
	return X.bestf;
}

template <class Type>
inline void Swap(Type &a, Type &b)
{ 
	Type temp=a; 
	a=b; 
	b=temp;
}

    由于算法Backtrack在每一个节点处耗费O(1)计算时间，故在最坏情况下，整个算法计算时间复杂性为O(n!)。程序运行结果如下：

     2、符号三角形问题

    (1)问题描速

    下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”，2个异号下面都是“-”。

    在一般情况下，符号三角形的第一行有n个符号。符号三角形问题要求对于给定的n，计算有多少个不同的符号三角形，使其所含的“+”和“-”的个数相同。

    (2)算法设计

    解向量：用n元组x[1:n]表示符号三角形的第一行。 当x[i]=1时表示符号三角形第一行的第i个符号为"+"；当i=0时，表示符号三角形第一行的第i个符号为"-"；1<=x<=n。由于x[i]是二值的，所以可以用一棵完全二叉树来表示解空间。
    可行性约束函数：在符号三角形的第一行前i个符号x[1:i]确定后，就确定了一个由i(i+1)/2个符号组成的符号三角形。下一步确定x[i+1]的值后，只要在前面已确定的符号三角形的右边加一条边，就可以扩展为x[1:i+1]所相应的符号三角形。最终由x[1:n]所确定的符号三角形中包含"+"号个数与"-"个数同为n(n+1)/4。因此，当前符号三角形所包含的“+”个数与“-”个数均不超过n*(n+1)/4 。
    无解的判断：对于给定的n，当n*(n+1)/2为奇数时，显然不存在包含的"+"号个数与"-"号个数相同的符号三角形。此时，可以通过简单的判断加以处理。 

    程序的具体代码如下：

#include "stdafx.h"
#include <iostream>
using namespace std;

class Triangle
{
    friend int Compute(int);
    private:
        void Backtrack(int i);
        int n,      //第一行的符号个数
            half,   //n*(n+1)/4
            count,  //当前"+"号个数
            **p;    //符号三角矩阵
        long sum;   //已找到的符号三角形数
};

int Compute(int n);

int main()
{
    for(int n=1;n<=10;n++)
    {
        cout<<"n="<<n<<"时，共有"<<Compute(n);
        cout<<"个不同的符号三角形。"<<endl;
    }
   return 0;
}

void Triangle::Backtrack(int t)
{
    if ((count>half)||(t*(t-1)/2-count>half))
    {
        return;
    }

    if (t>n)
    {
        sum++;
    }
    else
    {
        for (int i=0;i<2;i++)
        {
            p[1][t]=i;//第一行符号
            count+=i;//当前"+"号个数

            for(int j=2;j<=t;j++)
            {
                p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
                count+=p[j][t-j+1];
            }
            Backtrack(t+1);
            for (int j=2;j<=t;j++)
            {
                count-=p[j][t-j+1];
            }
            count-=i;
        }
    }
}

int Compute(int n)
{
    Triangle X;
    X.n=n;
    X.count=0;
    X.sum=0;

    X.half=n*(n+1)/2;
    if(X.half%2==1)return 0;
    X.half=X.half/2;

    int**p=new int*[n+1];

    for(int i=0;i<=n;i++)
    {
        p[i]=new int[n+1];
    }

    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            p[i][j]=0;
        }
    }

    X.p=p;
    X.Backtrack(1);
    for(int i=0;i<=n;i++)
    {
        delete []p[i];
    }
    delete []p;
    p=0;
    return X.sum;
}

#include "stdafx.h"
#include <iostream>
using namespace std; 

class Triangle 
{
	friend int Compute(int);
	private:
		void Backtrack(int i);
		int n,		//第一行的符号个数
			half,	//n*(n+1)/4
			count,	//当前"+"号个数
			**p;    //符号三角矩阵
		long sum;   //已找到的符号三角形数             
}; 

int Compute(int n);

int main()
{
	for(int n=1;n<=10;n++)
	{
		cout<<"n="<<n<<"时，共有"<<Compute(n);
		cout<<"个不同的符号三角形。"<<endl;
	}
   return 0;
}

void Triangle::Backtrack(int t)
{
	if ((count>half)||(t*(t-1)/2-count>half)) 
	{
		return;
	}

	if (t>n)
	{
		sum++;
	}
    else
	{
		for (int i=0;i<2;i++) 
		{
			p[1][t]=i;//第一行符号
			count+=i;//当前"+"号个数

			for(int j=2;j<=t;j++) 
			{
				p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
				count+=p[j][t-j+1];
			}
			Backtrack(t+1);
			for (int j=2;j<=t;j++)
			{
				count-=p[j][t-j+1];
			}
			count-=i;
		}
	}
}

int Compute(int n)
{
	Triangle X;
	X.n=n;
	X.count=0;
	X.sum=0;

	X.half=n*(n+1)/2;
	if(X.half%2==1)return 0;
	X.half=X.half/2;

	int**p=new int*[n+1];

	for(int i=0;i<=n;i++)
	{
		p[i]=new int[n+1];
	}

	for(int i=0;i<=n;i++)  
	{
		for(int j=0;j<=n;j++)
		{
			p[i][j]=0;
		}
	}

	X.p=p;
	X.Backtrack(1);
	for(int i=0;i<=n;i++)
	{
		delete []p[i];
	}
	delete []p;
	p=0;
	return X.sum;
}

     计算可行性约束需要O(n)时间，在最坏情况下有 O(2^n)个结点需要计算可行性约束，故解符号三角形问题的回溯算法所需的计算时间为 O(n2^n)。程序运行结果如图：