ACM-DFS之Prime Ring Problem——hdu1016
Prime Ring Problem
Problem Description
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
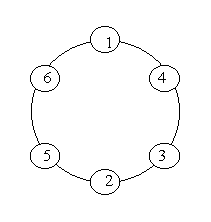
Note: the number of first circle should always be 1.

Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6 8
Sample Output
Case 1: 1 4 3 2 5 6 1 6 5 2 3 4 Case 2: 1 2 3 8 5 6 7 4 1 2 5 8 3 4 7 6 1 4 7 6 5 8 3 2 1 6 7 4 3 8 5 2 这是一道dfs(深搜)题目(废话。。), 题意就是求一个素数环,使得相邻两个数之和均为素数, 当然第一个与最后一个相加也要是素数,因为它是环嘛。 言归正传, 这道题解法就是建立两个数组,一个存数,一个用来判断某个数是否使用过, 还需要一个辅助数组,不能每一次都判断两个数相加的和是否为素数,每次都用函数算一遍,肯定超时的啦, 所以建立一个数组把前40的数字是否为素数状态存储起来,需要判断的时候,只需要读相应下标所对应的数就可以了, 每次搜索都遍历一遍,当然剪枝也减一下, 最后注意一下格式问题,最后一个数后面木有空格= =。#include <iostream> using namespace std; // 该数组用来存储,数组下标数字是否为素数状态,1则是素数 int prim[]={0,0,1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,1,0,0,0}; int arr[21],brr[21],n; void dfs(int js) { int i; // 剪枝,计数器不能大于输入的n if(js>n) return; // 若相等,则输出,注意输出格式 if(js==n) { for(i=0;i<n-1;++i) cout<<brr[i]<<" "; cout<<brr[n-1]<<endl; return; } for(i=2;i<=n;++i) { if(arr[i]==1) continue; if(js+1==n) { if(prim[brr[js-1]+i]==1 && prim[1+i]==1) { brr[js]=i; arr[i]=1; dfs(js+1); arr[i]=0; } } else { if(prim[brr[js-1]+i]==1) { brr[js]=i; arr[i]=1; dfs(js+1); arr[i]=0; } } } return; } int main() { int xh=1; while(cin>>n) { // 初始化两个数组 memset(brr,0,sizeof(brr)); memset(arr,0,sizeof(arr)); arr[0]=brr[0]=1; cout<<"Case "<<xh<<":"<<endl; dfs(1); cout<<endl; ++xh; } return 0; }