interviewstreet - even tree

题目来源：https://www.interviewstreet.com/challenges/dashboard/#problem/4fffc24df25cd

解题报告：

这道题求一颗树，最多可以去掉几条边，使得被分割成的每颗单独的树的节点个数都是偶数。题目蛮有意思，难度适宜。

首先，将输入转换为树的格式，对每个节点，保留它的父亲节点和儿子节点的编号。

然后遍历树的每个节点，得到以该节点为根的树的节点个数（包括该节点）

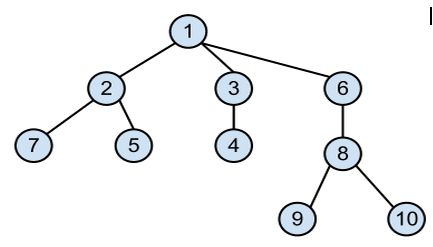
对一个节点R，设它有儿子节点A，如果以A为根的树的节点个数有偶数个，则代表R与A这条边可以被去除，否则不可以。这样依次查找每个节点，看它与它儿子的边是否可以被去除，最后得到最多可以删去多少条边。

/* Enter your code here. Read input from STDIN. Print output to STDOUT */
#include <iostream>
#include <queue>
using namespace std;

int sum[101]; //以i为根的树的节点个数
int s[101][101]; //s[i][j]=1代表j为i的儿子
int p[101];
int adj[101][101];
int k;

int getSum(int index)
{
    if (sum[index] != 0)
        return sum[index];
    int sm = 0;
    for (int i = 0; i <= 100; i++)
    {
        if(s[index][i] == 1)
        {
            sm += getSum(i);
        }
    }
    sm++;
    sum[index] = sm;
    return sm;
}

void findResult(int root)
{
    for (int i = 0; i <= 100; i++)
    {
        if (s[root][i] == 1)
        {
            if(getSum(i) % 2 == 0)
            {
                k++;
             }
			 findResult(i);
        }
    }
}

int main()
{
    int N, M;
    int root;
    cin >> N >> M;
    //initialization
    k = 0;
    for(int i = 0; i <= 100; i++)
    {
        sum[i] = 0;
        p[i] = -1;
        for (int j = 0; j <= 100; j++)
        {
            s[i][j] = 0;
            adj[i][j] = 0;
        }    
    }
    for (int i = 0; i < M; i++)
    {
        int node1, node2;
        cin >> node1 >> node2;
        if (i == 0)
            root = node1;
        adj[node1][node2] = 1;
        adj[node2][node1] = 1;
    }
    queue<int> q;
    q.push(root);
    while(!q.empty())
    {
        int node = q.front();
        q.pop();
        for (int i = 0; i <= 100; i++)
        {
            if (adj[node][i] == 1 && i!=p[node])
            {
                p[i] = node;
                s[node][i] = 1;
                q.push(i);
            }
        }
    }
    findResult(root);
    cout << k << endl;
    
}

附录：

You are given a tree (a simple connected graph with no cycles).You have to remove as many edges from the tree as possible to obtain a forest with the condition that : Each connected component of the forest contains even number of vertices

Your task is to calculate the number of removed edges in such a forest.

Input:
The first line of input contains two integers N and M. N is the number of vertices and M is the number of edges. 2 <= N <= 100. 
Next M lines contains two integers u_i and v_i which specifies an edge of the tree. (1-based index)

Output:
Print a single integer which is the answer

Sample Input 

10 9

2 1

3 1

4 3

5 2

6 1

7 2

8 6

9 8

10 8

 

Sample Output :

2

 

Explanation : On removing the edges (1, 3) and (1, 6), we can get the desired result.

Original tree: 


Decomposed tree:

Note: The tree in the input will be such that it can always be decomposed into components containing even number of nodes.