B树和B+树

 

动态查找树主要有：二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced Binary Search Tree），红黑树(Red-Black Tree )，B-tree/B⁺-tree/ B^*-tree (B~Tree)。前三者是典型的二叉查找树结构，其查找的时间复杂度O(log₂N)与树的深度相关，那么降低树的深度自然会提高查找效率

 ，B-tree就是指的B树

B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。那为什么又说B树与红黑树很相似呢?因为与红黑树一样，一棵含n个结点的B树的高度也为O（lgn），但可能比一棵红黑树的高度小许多，应为它的分支因子比较大。所以，B树可以在O（logn）时间内，实现各种如插入（insert），删除（delete）等动态集合操作。

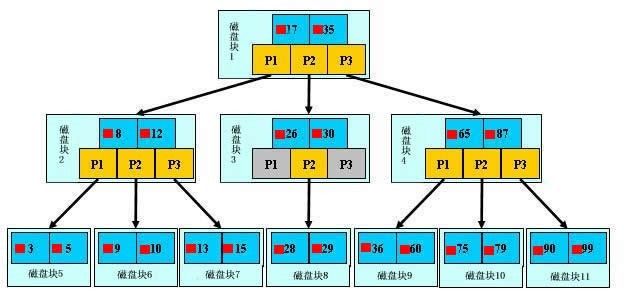
B 树又叫平衡多路查找树。一棵m阶的B 树 (m叉树)的特性如下：

1. 树中每个结点 最多含有m=2t个孩子（m>=2）；
2. 除根结点和叶子结点外，其它每个结点 至少有 [ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4. 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；
5. 每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：( n个关键字，n+1个子节点指针)
          a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。 
          b)   Pi为指向子树根的接点，且 指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。 
          c)   关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。

    针对上面第5点，再阐述下：B树中每一个结点能包含的关键字（如之前上面的D H和Q T X）数有一个上界和下界。这两个界可以用一个称作B树的最小度数（算法导论中文版上译作度数）t=m（t>=2）表示。

• 每个非根的结点必须至少含有t-1个关键字。 每个非根的内结点至少有t个子女。如果树是非空的，则根结点至少包含一个关键字；
• 每个结点可包含之多2t-1个关键字。所以 一个内结点至多可有2t个子女。如果一个结点恰好有2t-1个关键字，我们就说这个结点是满的（而稍后介绍的B*树作为B树的一种常用变形，B*树中要求每个内结点至少为2/3满，而不是像这里的B树所要求的至少半满）；
• 当关键字数t=2（t=2的意思是，tmin=2，t可以>=2）时的B树是最简单的 （有很多人会因此误认为B树就是二叉查找树，但二叉查找树就是二叉查找树，B树就是B树，B树的真正最准确的定义为：一棵含有t（t>=2）个关键字的平衡多路查找树 ）。每个内结点可能因此而含有2个、3个或4个子女，亦即一棵2-3-4树，然而在实际中，通常采用大得多的t值。

B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

#define MAXM 10   //B-树的最大阶数
typedef int KeyType;  //KeyType为关键字类型
typedef  struct  node
{int  keynum;          //结点中的关键字个数
 struct node * parent; //双亲结点指针
 keytype  key[MAXM];//关键字数组key[1…keynum],key[0]不用
 struct node *ptr[MAXM];//孩子结点指针数组ptr[0…keynum]
}BTNode;         //B-树结点类型

本篇文章来源于 中文DY豆-cn.dydou.cn 原文链接：http://dydou.cn/Linux/201008/0Q91A202010.html

 

4.B⁺-tree

B⁺-tree：是应文件系统所需而产生的一种B-tree的变形树。

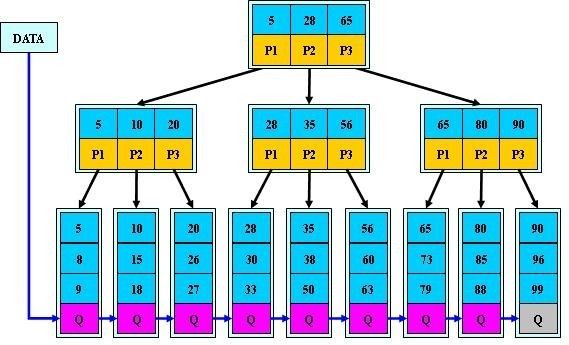
一棵m阶的B+树和m阶的B树的差异在于：

      1.有n棵子树的结点中含有n个关键字； (而B 树是n棵子树有n-1个关键字)

      2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)

      3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)

a)     为什么说B⁺-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

 

1) B⁺-tree的磁盘读写代价更低

B⁺-tree的内部结点并没有指向关键字具体信息的指针,那P1，P2是啥玩意。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

    举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B⁺ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B⁺ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

2) B⁺-tree的查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

 

 B+树的查找
在B+树中可以采用两种查找方式:
一是直接从最小关键字开始进行顺序查找;
另一种就是从B+树的根结点开始随即查找.这种查找方式与B-树的查找方法相似,只是在分支结点上的关键字与查找值相等时,查找并不结束,要继续查找叶子结点为止,此时若查找成功,则按所给指针取出对应记录即可
本篇文章来源于 中文DY豆-cn.dydou.cn 原文链接：http://dydou.cn/Linux/201008/0Q91A202010.html

 

B+树适合于顺序查找和随机查找，因为书里面一个指向从最小结点数值到最大结点数值的  指针，所以可以顺序查找