java常用排序算法总结<一>

这篇排序文章从思想 理解 到实现，然后到整理，花了我几天的时间，现把它记录于此，希望对大家有一定的帮助，写的不好的请不要见笑，写错了的，请指出来我更正。最后如果对你有一定的帮助，请回贴支持一下哦^_^ ！

申明： 排序算法思想来自互联网，代码自己实现，仅供参考。

• 插入排序

直接插入排序、希尔排序

• 选择排序

简单选择排序、堆排序

• 交换排序

冒泡排序、快速排序

• 归并排序

• 基数排序

排序基类

 package  sort;

 import  java.util.Arrays;
 import  java.util.Comparator;
 import  java.util.Random;

 /**
  * 排序接口，所有的排序算法都要继承该抽象类，并且要求数组中的
  * 元素要具有比较能力，即数组元素已实现了Comparable接口
  *
  * @author jzj
  * @date 2009-12-5
  *
  * @param <E>
  */
 public   abstract   class  Sort<E  extends  Comparable<E>> {

     public   final  Comparator<E> DEFAULT_ORDER =  new  DefaultComparator();
     public   final  Comparator<E> REVERSE_ORDER =  new  ReverseComparator();

     /**
      * 排序算法，需实现，对数组中指定的元素进行排序
      * @param array 待排序数组
      * @param from 从哪里
      * @param end 排到哪里
      * @param c
      */
     public   abstract   void  sort(E[] array,  int  from,  int  end, Comparator<E> c);

     /**
      * 对数组中指定部分进行排序
      * @param from 从哪里
      * @param len 排到哪里
      * @param array 待排序数组
      * @param c 比较器
      */
     public   void  sort( int  from,  int  len, E[] array, Comparator<E> c) {
         sort(array, 0 , array.length -  1 , c);
     }

     /**
      * 对整个数组进行排序，可以使用自己的排序比较器，也可使用该类提供的两个比较器
      * @param array 待排序数组
      * @param c 比较器
      */
     public   final   void  sort(E[] array, Comparator<E> c) {
         sort(0 , array.length, array, c);
     }

     /**
      * 对整个数组进行排序，采用默认排序比较器
      * @param array 待排序数组
      */
     public   final   void  sort(E[] array) {
         sort(0 , array.length, array,  this .DEFAULT_ORDER);
     }

     //默认比较器（一般为升序，但是否真真是升序还得看E是怎样实现Comparable接口的）
     private   class  DefaultComparator  implements  Comparator<E> {
         public   int  compare(E o1, E o2) {
             return  o1.compareTo(o2);
         }
     }

     //反序比较器，排序刚好与默认比较器相反
     private   class  ReverseComparator  implements  Comparator<E> {
         public   int  compare(E o1, E o2) {
             return  o2.compareTo(o1);
         }
     }

     /**
      * 交换数组中的两个元素的位置
      * @param array 待交换的数组
      * @param i 第一个元素
      * @param j 第二个元素
      */
     protected   final   void  swap(E[] array,  int  i,  int  j) {
         if  (i != j) { //只有不是同一位置时才需交换
             E tmp = array[i];
             array[i] = array[j];
             array[j] = tmp;
         }
     }

     /**
      * 数组元素后移
      * @param array 待移动的数组
      * @param startIndex 从哪个开始移
      * @param endIndex 到哪个元素止
      */
     protected   final   void  move(E[] array,  int  startIndex,  int  endIndex) {
         for  ( int  i = endIndex; i >= startIndex; i--) {
             array[i + 1 ] = array[i];
         }
     }

     /**
      * 以指定的步长将数组元素后移，步长指定每个元素间的间隔
      * @param array 待排序数组
      * @param startIndex 从哪里开始移
      * @param endIndex 到哪个元素止
      * @param step 步长
      */
     protected   final   void  move(E[] array,  int  startIndex,  int  endIndex,  int  step) {
         for  ( int  i = endIndex; i >= startIndex; i -= step) {
             array[i + step] = array[i];
         }
     }

     //测试方法
     @SuppressWarnings ( "unchecked" )
     public   static   final  <E  extends  Comparable<E>>  void  testSort(Sort<E> sorter, E[] array) {

         if  (array ==  null ) {
             array = randomArray();
         }
         //为了第二次排序，需拷贝一份
         E[] tmpArr = (E[]) new  Comparable[array.length];
         System.arraycopy(array, 0 , tmpArr,  0 , array.length);

         System.out.println("源 - "  + Arrays.toString(tmpArr));

         sorter.sort(array, sorter.REVERSE_ORDER);
         System.out.println("降 - "  + Arrays.toString(array));

         sorter.sort(tmpArr, sorter.DEFAULT_ORDER);
         System.out.println("升 - "  + Arrays.toString(tmpArr));
     }

     //生成随机数组
     @SuppressWarnings ( "unchecked" )
     private   static  <E  extends  Comparable<E>> E[] randomArray() {
         Random r = new  Random(System.currentTimeMillis());
         Integer[] a = new  Integer[r.nextInt( 30 )];
         for  ( int  i =  0 ; i < a.length; i++) {
             a[i] = new  Integer(r.nextInt( 100 ));
         }
         return  (E[]) a;
     }
 }

插入排序

直接插入排序

 

一般直接插入排序的时间复杂度为O ( n^2 ) ，但是当数列基本有序时，如果按照有数列顺序排时，时间复杂度将改善到O( n )，另外，因直接插入排序算法简单，如果待排序列规模不很大时效率也较高。

 

在已经排好序的序列中查找待插入的元素的插入位置，并将待插入元素插入到有序列表中的过程。
 
将数组分成两部分，初始化时，前部分数组为只有第一个元素，用来存储已排序元素，我们这里叫 arr1 ；后部分数组的元素为除第一个元素的所有元素，为待排序或待插入元素，我们这里叫 arr2 。
排序时使用二层循环：第一层对 arr2 进行循环，每次取后部分数组（待排序数组）里的第一个元素（我们称为待排序元素或称待插入元素） e1 ，然后在第二层循环中对 arr1 （已排好序的数组）从第一个元素往后进行循环，查到第一个大于待插入元素（如果是升序排列）或第一个小于待插入元素（如果是降序排列） e2 ，然后对 arr1 从 e2 元素开始往后的所有元素向后移，最后把 e1 插入到原来 e2 所在的位置。这样反复地对 arr2 进行循环，直到 arr2 中所有的待插入的元素都插入到 arr1 中。

 package  sort;

 import  java.util.Comparator;

 /**
  *  直接插入排序算法
  * @author jzj
  * @date 2009-12-5
  *
  * @param <E>
  */
 public   class  InsertSort<E  extends  Comparable<E>>  extends  Sort<E> {

     /**
      * 排序算法的实现，对数组中指定的元素进行排序
      * @param array 待排序的数组
      * @param from 从哪里开始排序
      * @param end 排到哪里
      * @param c 比较器
      */
     public   void  sort(E[] array,  int  from,  int  end, Comparator<E> c) {

         /*
          * 第一层循环：对待插入（排序）的元素进行循环
          * 从待排序数组断的第二个元素开始循环，到最后一个元素（包括）止
          */
         for  ( int  i = from +  1 ; i <= end; i++) {
             /*
              * 第二层循环：对有序数组进行循环，且从有序数组最第一个元素开始向后循环
              * 找到第一个大于待插入的元素
              * 有序数组初始元素只有一个，且为源数组的第一个元素，一个元素数组总是有序的
              */
             for  ( int  j =  0 ; j < i; j++) {
                 E insertedElem = array[i];//待插入到有序数组的元素
                 //从有序数组中最一个元素开始查找第一个大于待插入的元素
                 if  (c.compare(array[j], insertedElem) >  0 ) {
                     //找到插入点后，从插入点开始向后所有元素后移一位
                     move(array, j, i - 1 );
                     //将待排序元素插入到有序数组中
                     array[j] = insertedElem;
                     break ;
                 }
             }
         }

         //=======以下是java.util.Arrays的插入排序算法的实现
         /*
          * 该算法看起来比较简洁一j点，有点像冒泡算法。
          * 将数组逻辑上分成前后两个集合，前面的集合是已经排序好序的元素，而后面集合为待排序的
          * 集合，每次内层循从后面集合中拿出一个元素，通过冒泡的形式，从前面集合最后一个元素开
          * 始往前比较，如果发现前面元素大于后面元素，则交换，否则循环退出
          *
          * 总感觉这种算术有点怪怪，既然是插入排序，应该是先找到插入点，而后再将待排序的元素插
          * 入到的插入点上，那么其他元素就必然向后移，感觉算法与排序名称不匹，但返过来与上面实
          * 现比，其实是一样的，只是上面先找插入点，待找到后一次性将大的元素向后移，而该算法却
          * 是走一步看一步，一步一步将待排序元素往前移
          */
         /*
         for (int i = from; i <= end; i++) {
             for (int j = i; j > from && c.compare(array[j - 1], array[j]) > 0; j--) {
                 swap(array, j, j - 1);
             }
         }
         */
     }

     /**
      * 测试
      * @param args
      */
     public   static   void  main(String[] args) {
         Integer[] intgArr = { 5 ,  9 ,  1 ,  4 ,  1 ,  2 ,  6 ,  3 ,  8 ,  0 ,  7  };
         InsertSort<Integer> insertSort = new  InsertSort<Integer>();
         Sort.testSort(insertSort, intgArr);
         Sort.testSort(insertSort, null );
     }
 }

插入排序算法对于大数组，这种算法非常慢。但是对于小数组，它比其他算法快。其他算法因为待的数组元素很少，反而使得效率降低。在Java集合框架 中，排序都是借助于java.util.Arrays来完成的，其中排序算法用到了插入排序、快速排序、归并排序。插入排序用于元素个数小于7的子数组排 序，通常比插入排序快的其他排序方法，由于它们强大的算法是针对大数量数组设计的，所以元素个数少时速度反而慢。

希尔排序

希尔思想介绍

希尔算法的本质是缩小增量排序，是对直接插入排序算法的改进。一般直接插入排序的时间复杂度为O ( n^2 ) ，但是当数列基本有序时，如果按照有数列顺序排时，时间复杂度将改善到O( n )，另外,因直接插入排序算法简单,如果待排序列规模不很大时效率也较高，Shell 根据这两点分析结果进行了改进，将待排记录序列以一定的增量间隔h 分割成多个子序列，对每个子序列分别进行一趟直接插入排序, 然后逐步减小分组的步长h ，对于每一个步长h 下的各个子序列进行同样方法的排序,直到步长为1 时再进行一次整体排序。
因为不管记录序列多么庞大,关键字多么混乱,在先前较大的分组步长h 下每个子序列的规模都不大，用直接插入排序效率都较高。 尽管在随后的步长h 递减分组中子序列越来越大，但由于整个序列的有序性也越来越明显，则排序效率依然较高。这种改进抓住了直接插入排序的两点本质，大大提高了它的时间效率。

希尔增量研究

综上所述：

(1) 希尔排序的核心是以某个增量h 为步长跳跃分组进行插入排序，由于分组的步长h 逐步缩小，所以也叫“缩小增量排序”插入排序。其关键是如何选取分组的步长序列ht ,. . . , hk ,. . . , h1 , h0 才能使得希尔方法的时间效率最高；

(2) 待排序列记录的个数n 、跳跃分组步长逐步减小直到为1时所进行的扫描次数T、增量的和、记录关键字比较的次数以及记录移动的次数或各子序列中的反序数等因素都影响希尔算法的时间复杂度：其中记录关键字比较的次数是重要因素，它主要取决于分组步长序列的选择；

(3) 希尔方法是一种不稳定排序算法，因为其排序过程中各趟的步长不同，在第k 遍用hk作为步长排序之后，第k +1 遍排序时可能会遇到多个逆序存在，影响排序的稳定性。

 

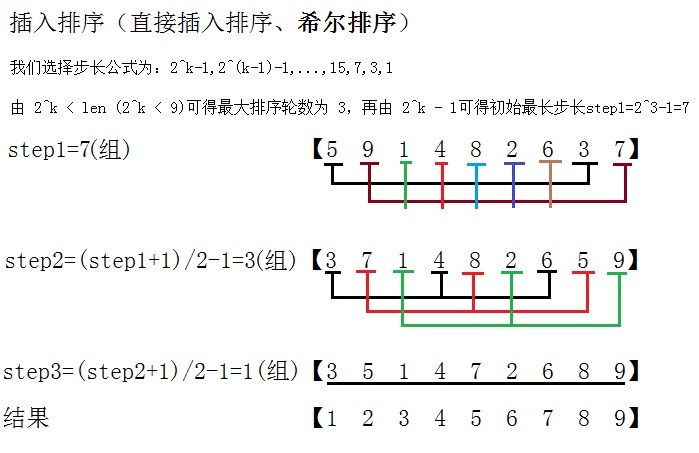
试验结果表明,SHELL 算法的时间复杂度受增量序列的影响明显大于其他因素，选取恰当的增量序列能明显提高排序的时间效率，我们认为第k 趟排序扫描的增量步长为 2^k - 1 ,即增量序列为. . . 2^k - 1 ,. . . ,15 ,7 ,3 ,1时较为理想，但它并不是唯一的最佳增量序列，这与其关联函数目前尚无确定解的理论结果是一致的。

 package  sort;

 import  java.util.Comparator;

 /**
  * 希尔排序算法
  * @author jzj
  * @date 2009-12-5
  *
  * @param <E>
  */
 public   class  ShelltSort<E  extends  Comparable<E>>  extends  Sort<E> {

     /**
      * 排序算法的实现，对数组中指定的元素进行排序
      * @param array 待排序的数组
      * @param from 从哪里开始排序
      * @param end 排到哪里
      * @param c 比较器
      */
     public   void  sort(E[] array,  int  from,  int  end, Comparator<E> c) {
         //初始步长，实质为每轮的分组数
         int  step = initialStep(end - from +  1 );

         //第一层循环是对排序轮次进行循环。(step + 1) / 2 - 1 为下一轮步长值
         for  (; step >=  1 ; step = (step +  1 ) /  2  -  1 ) {
             //对每轮里的每个分组进行循环
             for  ( int  groupIndex =  0 ; groupIndex < step; groupIndex++) {

                 //对每组进行直接插入排序
                 insertSort(array, groupIndex, step, end, c);
             }
         }
     }

     /**
      * 直接插入排序实现
      * @param array 待排序数组
      * @param groupIndex 对每轮的哪一组进行排序
      * @param step 步长
      * @param end 整个数组要排哪个元素止
      * @param c 比较器
      */
     private   void  insertSort(E[] array,  int  groupIndex,  int  step,  int  end, Comparator<E> c) {
         int  startIndex = groupIndex; //从哪里开始排序
         int  endIndex = startIndex; //排到哪里
         /*
          * 排到哪里需要计算得到，从开始排序元素开始，以step步长，可求得下元素是否在数组范围内，
          * 如果在数组范围内，则继续循环，直到索引超现数组范围
          */
         while  ((endIndex + step) <= end) {
             endIndex += step;
         }

         // i为每小组里的第二个元素开始
         for  ( int  i = groupIndex + step; i <= end; i += step) {
             for  ( int  j = groupIndex; j < i; j += step) {
                 E insertedElem = array[i];
                 //从有序数组中最一个元素开始查找第一个大于待插入的元素
                 if  (c.compare(array[j], insertedElem) >=  0 ) {
                     //找到插入点后，从插入点开始向后所有元素后移一位
                     move(array, j, i - step, step);
                     array[j] = insertedElem;
                     break ;
                 }
             }
         }
     }

     /**
      * 根据数组长度求初始步长
      *
      * 我们选择步长的公式为：2^k-1,2^(k-1)-1,...,15,7,3,1 ，其中2^k 减一即为该步长序列，k
      * 为排序轮次
      *
      * 初始步长：step = 2^k-1
      * 初始步长约束条件：step < len - 1 初始步长的值要小于数组长度还要减一的值（因
      * 为第一轮分组时尽量不要分为一组，除非数组本身的长度就小于等于4）
      *
      * 由上面两个关系试可以得知：2^k - 1 < len - 1 关系式，其中k为轮次，如果把 2^k 表 达式
      * 转换成 step 表达式，则 2^k-1 可使用 (step + 1)*2-1 替换（因为 step+1 相当于第k-1
      * 轮的步长，所以在 step+1 基础上乘以 2 就相当于 2^k 了），即步长与数组长度的关系不等式为
      * (step + 1)*2 - 1 < len -1
      *
      * @param len 数组长度
      * @return
      */
     private   static   int  initialStep( int  len) {
         /*
          * 初始值设置为步长公式中的最小步长，从最小步长推导出最长初始步长值，即按照以下公式来推:
          * 1,3,7,15,...,2^(k-1)-1,2^k-1
          * 如果数组长度小于等于4时，步长为1，即长度小于等于4的数组不且分组，此时直接退化为直接插
          * 入排序
          */
         int  step =  1 ;

         //试探下一个步长是否满足条件，如果满足条件，则步长置为下一步长
         while  ((step +  1 ) *  2  -  1  < len -  1 ) {
             step = (step + 1 ) *  2  -  1 ;
         }

         System.out.println("初始步长 - "  + step);
         return  step;
     }

     /**
      * 测试
      * @param args
      */
     public   static   void  main(String[] args) {
         Integer[] intgArr = { 5 ,  9 ,  1 ,  4 ,  8 ,  2 ,  6 ,  3 ,  7 ,  10  };
         ShelltSort<Integer> shellSort = new  ShelltSort<Integer>();
         Sort.testSort(shellSort, intgArr);
         Sort.testSort(shellSort, null );
     }
 }

选择排序

简单选择排序

每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。
选择排序不像冒泡排序算法那样先并不急于调换位置，第一轮（k=1）先从array[k]开始逐个检查，看哪个数最小就记下该数所在的位置于 minlIndex中，等一轮扫描完毕，如果找到比array[k-1]更小的元素，则把array[minlIndex]和a[k-1]对调，这时 array[k]到最后一个元素中最小的元素就换到了array[k-1]的位置。 如此反复进行第二轮、第三轮…直到循环至最后一元素

 package  sort;

 import  java.util.Comparator;

 /**
  * 简单选择排序算法
  * @author jzj
  * @date 2009-12-5
  *
  * @param <E>
  */
 public   class  SelectSort<E  extends  Comparable<E>>  extends  Sort<E> {

     /**
      * 排序算法的实现，对数组中指定的元素进行排序
      * @param array 待排序的数组
      * @param from 从哪里开始排序
      * @param end 排到哪里
      * @param c 比较器
      */
     public   void  sort(E[] array,  int  from,  int  end, Comparator<E> c) {
         int  minlIndex; //最小索引
         /*
          * 循环整个数组（其实这里的上界为 array.length - 1 即可，因为当 i= array.length-1
          * 时，最后一个元素就已是最大的了，如果为array.length时，内层循环将不再循环），每轮假设
          * 第一个元素为最小元素，如果从第一元素后能选出比第一个元素更小元素，则让让最小元素与第一
          * 个元素交换
          */
         for  ( int  i = from; i <= end; i++) {
             minlIndex = i;//假设每轮第一个元素为最小元素
             //从假设的最小元素的下一元素开始循环
             for  ( int  j = i +  1 ; j <= end; j++) {
                 //如果发现有比当前array[smallIndex]更小元素，则记下该元素的索引于smallIndex中
                 if  (c.compare(array[j], array[minlIndex]) <  0 ) {
                     minlIndex = j;
                 }
             }

             //先前只是记录最小元素索引，当最小元素索引确定后，再与每轮的第一个元素交换
             swap(array, i, minlIndex);
         }
     }

     /**
      * 测试
      * @param args
      */
     public   static   void  main(String[] args) {
         Integer[] intgArr = { 5 ,  9 ,  1 ,  4 ,  1 ,  2 ,  6 ,  3 ,  8 ,  0 ,  7  };
         SelectSort<Integer> insertSort = new  SelectSort<Integer>();
         Sort.testSort(insertSort, intgArr);
         Sort.testSort(insertSort, null );
     }
 }

堆排序

堆实质上是满足如下性质的完全二叉树：树中任一非叶结点的关键字均不大于(或不小于)其左右孩子(若存在)结点的关键字。

【例】关键字序列(10，15，56，25，30，70)和(70，56，30，25，15，10)分别满足堆性质(1)和(2)，故它们均是堆，其对应的完全二叉树分别如小根堆示例和大根堆示例所示：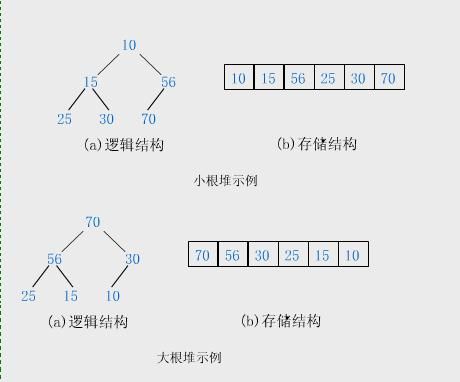

根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最小者的堆称为小顶堆。
根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最大者，称为大顶堆。

堆是一种完全二叉树，一般使用数组来实现。堆排序也是一种选择性的排序，每次选择第i大的元素。

 

另外排序过程中借助了堆结构，堆就是一种完全二叉树，所以这里先要熟悉要用的二叉树几个性质：

N（N>1）个节点的的完全二叉树从层次从左自右编号，最后一个分枝节点（非叶子节点）的编号为 N/2 取整。

且对于编号 i（1<=i<=N）有：父节点为 i/2 向下取整；若2i>N，则节点i没有左孩子，否则其左孩子为2i；若2i+1>N，则没有右孩子，否则其右孩子为2i+1。

注，这里使用完全二叉树只是为了好描述算法，它只是一种逻辑结构，真真在实现时我们还是使用数组来存储这棵二叉树的，因为完全二叉树完全可以使用数组来存储。

 

算法描述：

堆排序其实最主要的两个过程：第一步，创建初始堆；第二步，交换根节点与最后一个非叶子节

第一步实现 ：从最后一个非叶子节点为开始向前循环每个会支节点，比较每个分支节点与他左右子节点，如果其中某个子节点比父节点大，则与父节点交换，交换后原父节点可 能还小于原子节点的子节点，所以还需对原父节点进行调整，使用原父节点继续下沉，直到没有子节点或比左右子节点都大为止，调用过程可通过递归完成。当某个 非叶子节点调整完毕后，再处理下一个非叶子节点，直到根节点也调整完成，这里初始堆就创建好了，这里我们创建的是大顶堆，即大的元素向树的根浮，这样排序 最后得到的结果为升序，因为最大的从树中去掉，并从数组最后往前存放。

第二步实现 ：将树中的最后一个元素与堆顶元素进行交换，并从树中去掉最后叶子节点。交换后再按创建初始堆的算法调整根节点，如此下去直到树中只有一个节点为止。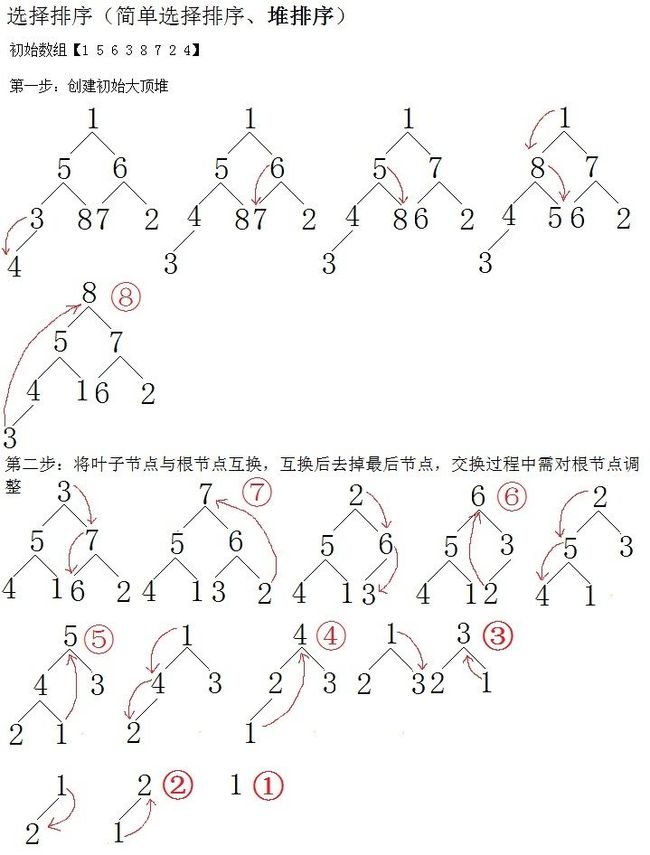

 

 package  sort;

 import  java.util.Comparator;

 public   class  HeapSort<E  extends  Comparable<E>>  extends  Sort<E> {

     /**
      * 排序算法的实现，对数组中指定的元素进行排序
      * @param array 待排序的数组
      * @param from 从哪里开始排序
      * @param end 排到哪里
      * @param c 比较器
      */
     public   void  sort(E[] array,  int  from,  int  end, Comparator<E> c) {
         //创建初始堆
         initialHeap(array, from, end, c);

         /*
          * 对初始堆进行循环，且从最后一个节点开始，直接树只有两个节点止
          * 每轮循环后丢弃最后一个叶子节点，再看作一个新的树
          */
         for  ( int  i = end - from +  1 ; i >=  2 ; i--) {
             //根节点与最后一个叶子节点交换位置，即数组中的第一个元素与最后一个元素互换
             swap(array, from, i - 1 );
             //交换后需要重新调整堆
             adjustNote(array, 1 , i -  1 , c);
         }

     }

     /**
      * 初始化堆
      * 比如原序列为：7,2,4,3,12,1,9,6,8,5,10,11
      * 则初始堆为：1,2,4,3,5,7,9,6,8,12,10,11
      * @param arr 排序数组
      * @param from 从哪
      * @param end 到哪
      * @param c 比较器
      */
     private   void  initialHeap(E[] arr,  int  from,  int  end, Comparator<E> c) {
         int  lastBranchIndex = (end - from +  1 ) /  2 ; //最后一个非叶子节点
         //对所有的非叶子节点进行循环 ，且从最一个非叶子节点开始
         for  ( int  i = lastBranchIndex; i >=  1 ; i--) {
             adjustNote(arr, i, end - from + 1 , c);
         }
     }

     /**
      * 调整节点顺序，从父、左右子节点三个节点中选择一个最大节点与父节点转换
      * @param arr 待排序数组
      * @param parentNodeIndex 要调整的节点，与它的子节点一起进行调整
      * @param len 树的节点数
      * @param c 比较器
      */
     private   void  adjustNote(E[] arr,  int  parentNodeIndex,  int  len, Comparator<E> c) {
         int  minNodeIndex = parentNodeIndex;
         //如果有左子树，i * 2为左子节点索引
         if  (parentNodeIndex *  2  <= len) {
             //如果父节点小于左子树时
             if  (c.compare(arr[parentNodeIndex -  1 ], arr[parentNodeIndex *  2  -  1 ]) <  0 ) {
                 minNodeIndex = parentNodeIndex * 2 ; //记录最大索引为左子节点索引
             }

             // 只有在有或子树的前提下才可能有右子树，再进一步断判是否有右子树
             if  (parentNodeIndex *  2  +  1  <= len) {
                 //如果右子树比最大节点更大
                 if  (c.compare(arr[minNodeIndex -  1 ], arr[(parentNodeIndex *  2  +  1 ) -  1 ]) <  0 ) {
                     minNodeIndex = parentNodeIndex * 2  +  1 ; //记录最大索引为右子节点索引
                 }
             }
         }

         //如果在父节点、左、右子节点三都中，最大节点不是父节点时需交换，把最大的与父节点交换，创建大顶堆
         if  (minNodeIndex != parentNodeIndex) {
             swap(arr, parentNodeIndex - 1 , minNodeIndex -  1 );
             //交换后可能需要重建堆，原父节点可能需要继续下沉
             if  (minNodeIndex *  2  <= len) { //是否有子节点，注，只需判断是否有左子树即可知道
                 adjustNote(arr, minNodeIndex, len, c);
             }
         }
     }

     /**
     * 测试
     * @param args
     */
     public   static   void  main(String[] args) {
         Integer[] intgArr = { 7 ,  2 ,  4 ,  3 ,  12 ,  1 ,  9 ,  6 ,  8 ,  5 ,  10 ,  11  };
         HeapSort<Integer> sort = new  HeapSort<Integer>();
         HeapSort.testSort(sort, intgArr);
         HeapSort.testSort(sort, null );
     }

 }