深入源码看数据结构(再探集合框架)
从源码的高度来看看集合中各个实现类的是如何组织我们存进去的数据的,主要包括Java类库中提供的几个具体的类:
LinkedList
ArrayList
HashMap
HashSet
TreeMap
TreeSet
PriorityQueue(顺序按下面的讲解顺序)
-----------------------------------------------------------------------------------------------------
1、java.util.LinkedList<E>
当我们创建一个LinkedList类的对象,并且试图增加一个新的元素的时候,到底是如何组织我们传进去的数据的呢?
//创建一个LinkedList类型的对象 java.util.LinkedList<String> l=new java.util.LinkedList<String>(); l.add(e);//e为E类的对象
打开add方法的源码看看:
public boolean add(E e) {
//调用LinkedList的私有方法
//header是LinkedList中的一个属性,这样定义的private transient Entry<E> //header = new Entry<E>(null, null, null);
addBefore(e, header);
return true;
}
//被调用的私有方法
private Entry<E> addBefore(E e, Entry<E> entry) {
Entry<E> newEntry = new Entry<E>(e, entry, entry.previous);
newEntry.previous.next = newEntry;
newEntry.next.previous = newEntry;
size++;
modCount++;
return newEntry;
}
//Entry<E>是LinkedList的内部类,包装每一个E类型的对象e,形成一个链表
private static class Entry<E> {
E element;
Entry<E> next;
Entry<E> previous;
Entry(E element, Entry<E> next, Entry<E> previous) {
this.element = element;
this.next = next;
this.previous = previous;
}
}
我们惊喜的发现,原来就是把我们传去的e对象包装成了Entry<E>,然后通过Entry<E>的next和previous两个
属性形成了一个以包装后的e对象(即Entry<E>)为节点的双向链表。
于是我们彻底 明白了LinkedList果然名副其实,就是一个链表嘛!
-----------------------------------------------------------------------------------------------------
2、java.util.ArrayList<E>
我们看看在ArrayList对象调用add();方法时,底层到底是如何执行的
public boolean add(E e) {
ensureCapacity(size + 1); // size是ArrayList中元素的个数
elementData[size++] = e; //在调整后的elementData末尾加入新的元素
return true;
}
public void ensureCapacity(int minCapacity) {
modCount++;
//elementData就是ArrayList中一个数组类型的属性,用来放进去的元素: //Object[] elementData
int oldCapacity = elementData.length;
if (minCapacity > oldCapacity) {//原来的elementData空间不够用了!
Object oldData[] = elementData;
int newCapacity = (oldCapacity * 3)/2 + 1;
//如果通过oldCapacity 计算出的新空间依然不够用
if (newCapacity < minCapacity)
newCapacity = minCapacity;
// minCapacity is usually close to size, so this is a win:
//这一步最后会调用System.arraycopy(original, 0, copy, 0,
Math.min(original.length, newLength));
//来实现将所有的元素copy到长度更大的数组中,这一步将很费时间
elementData = Arrays.copyOf(elementData, newCapacity);
}
}
于是我们发现:原 来ArrayList也是如名字说的,用Array组织数据。不过它内部定义的那个调整elementData数组的方法copy太多,
显然当数据量大的时候,性能不会很好。
-----------------------------------------------------------------------------------------------------
3、java.util.HashMap<K,V>
//向HashMap中插入键值对
public V put(K key, V value) {
if (key == null) //如果没有输入的key是null值
return putForNullKey(value);//插在Entry[0]的第一个,返回null
//获得哈希码
//1、首先用key类定义的hashcode()方法计算得到一个int
//2、进行一些>>>和^的操作
int hash = hash(key.hashCode());
//通过&运算将hash按二进制位取反(1变为0,0变为1)
//得到要插入的元素在table中的index
int i = indexFor(hash, table.length);
//遍历table[i]数据元下拖带的一个链表的所有元素
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
//如果有一个已经存在的元素的哈希码"=="为true,
//并且key值"=="或者"equals"为true
//也就是所谓的key经过hashcode()的一系列运算和
//equals()的一系列运算相同的元素,就替换原来的value
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
//把原来在table[i]位置的元素挤到Entry<K,V>的next位置
addEntry(hash, key, value, i);
return null;
}
}
想必大家看这段代码都看到晕了吧,为了让大家能够更加形象的人知道HashMap对数据的的组织形式,上了一个HaspMap数据结构图:
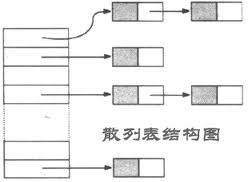
这里解释一下,这个图的最左边的一些就是上面源码中的table也就是HashMap的一个属性Entry[] table。
将一个新的键值对插入需要经过这几步:
---给key值计算哈码(计算在这一步int hash = hash(key.hashCode());),
---得出在table数组的中index:int i = indexFor(hash, table.
length);
---将键值对插入index确定的上图所示的一个横向的链表中。如果在这个链表中有要插入的pair的key经过hashcode()的
一系列运算和equals()的一系列运算相同的元素,就替换原来的value。(这也就是我们自己定义的类要用到HashMap
存储的时候,必须重写hashcode()和equals()方法,并且要保证对同一对象两个方法计算结果要相同的原因。
因为如果不相同,在一个同一对象为key插入值的时候就不会像你期望的那样后插入的value覆盖前面的value了,
而是会重新开辟一个空间存储)
于是,到这里我们明白了, 原来HashMap就是通过散列表这种数据结构组织数据的!
-----------------------------------------------------------------------------------------------------
4、java.util.HashSet<E>
public boolean add(E e) {
//map是该类的一个属性,这样定义的:HashMap<E,Object> map
//这里e作为key了
//value用本类的属性代替private static final Object PRESENT = new Object();每个键值对都相同
return map.put(e, PRESENT)==null;
}
小样直接自己不解决,抛给HashMap类的put()方法,也就是 用一个散列表存数据。详解见第三条对HashMap的讲解
-----------------------------------------------------------------------------------------------------
5、java.util.TreeMap<E>
public V put(K key, V value) {
Entry<K,V> t = root;//root是整棵树的根节点
if (t == null) {
//插入的第一个元素会成为根节点
root = new Entry<K,V>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// 调用Comparator的compare()方法确定新加的元素出现的位置。
//我们可以再自己定义的类中实现Comparator接口,然后传给树集的构造器。从而按照自己定义的不同的比较规则来给
整个树的数据进行排序。
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//这里我们将传进来的数据包装成Entry<K,V> ,通过Entry<K,V> 内部类的//属性 Entry<K,V> parent来组织一棵树
Entry<K,V> e = new Entry<K,V>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
我们又可以开心的大笑了,原来就是如此简单,就是 按照一定的规律形成一棵二叉树来存数据。
大笑过后,我们再次静下心来观察,源码中出现了这样一句:k.compareTo(t.key);是说用key对应的类中实现
的compareTo()方法来判断两个key的先后顺序。有若干标准的java平台类都实现了Compatable接口(Compatator可
以自己定义不同的比较规则,不过这个接口的比较规则只有一个,是定义key的类的时候定义的,没有可变性),如String类:
//用字典式排序。不展开分析了。
public int compareTo(String anotherString) {
int len1 = count;
int len2 = anotherString.count;
int n = Math.min(len1, len2);
char v1[] = value;
char v2[] = anotherString.value;
int i = offset;
int j = anotherString.offset;
if (i == j) {
int k = i;
int lim = n + i;
while (k < lim) {
char c1 = v1[k];
char c2 = v2[k];
if (c1 != c2) {
return c1 - c2;
}
k++;
}
} else {
while (n-- != 0) {
char c1 = v1[i++];
char c2 = v2[j++];
if (c1 != c2) {
return c1 - c2;
}
}
}
return len1 - len2;
}
所以,我们自己定义key的类的时候,要特别注意compareTo()方法中算法的选择,以便有一个最好的插入、查找、
遍历的性能。一般而言将元素添加到树集的速度快于数组和链表,慢于散列表(素服比较:数组、链表<树集<散列表)。
-----------------------------------------------------------------------------------------------------
6、java.util.TreeSet<E>
public boolean add(E e) {
return m.put(e, PRESENT)==null;
}
相信大家看到源码立马就能明白了吧,向HashSet一样TreeSet也偷懒了(至于为什么要偷懒,感兴趣的朋友可以去研究,
这里不展开了), 也是用二叉树的结构存数据,不多说!
-----------------------------------------------------------------------------------------------------
7、java.util.PriorityQueue<E>
我们看看调用add()方法在底层到底发生了什么事情!
public boolean add(E e) {
return offer(e);
}
public boolean offer(E e) {
//前面这的几行无非就是判断非空,判断本类的属性queue的长度是否够用然后做相应调整
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);
size = i + 1;
//最后终于要将元素插进去了
//如果queue空就插在index为0的位置,很好理解
//否则调用siftUp()方法(第一个参数是the position to fill,第二个参数是the element to insert)
if (i == 0)
queue[0] = e;
else
siftUp(i, e);
return true;
}
//再来看看siftUp()方法是如何实现的
//api文档的注释的意思是:将x插入合适的位置保持heap的有序性不变
//排序标准有两种途径获取:
//1、在构造PriorityQueue的时候传入的Comparator ,这个优先选用
//2、 要插入的x自己实现的compareTo方法
private void siftDown(int k, E x) {
if (comparator != null)
siftDownUsingComparator(k, x);
else
siftDownComparable(k, x);
}
//这里我只需分析comparator的情况就可以了
private void siftUpUsingComparator(int k, E x) {
//最坏的情况是:我找了一圈发现x才是整棵树种最小的。这时k为0,也就是到达整个堆的最小的元素
(或者整棵树的根节点),停止循环。
while (k > 0) {
//第一句的意思是获得要插入的这个k位置在queue中对应的父元素的索引
//我可以告诉大家这个式子的计算结果是:queue[n]节点的子节点是queue[2*n+1]和queue[2*(n+1)]
int parent = (k - 1) >>> 1;
Object e = queue[parent];
//如果比较规则确定x"大于"父节点,就插在k位置了,跳出循环
if (comparator.compare(x, (E) e) >= 0)
break;
//如果发现x较小,就将父节点的元素移到这个k位置
queue[k] = e;
k = parent;//现在要插入的位置变为原来父节点的位置
}
queue[k] = x;//
}
嗯,这个类用了一种“堆”(逻辑上是二叉树,存储上用数组,树中的元素有大小关系,越小在数组中的index也越小)
的数据结构。
典型应用是存储有优先级的任务,因为每次调用remove移除最小的元素(优先级最高的元素),都会自动排序,
保证每次移除的都是优先级最高的任务。 同样,TreeMap逻辑上也是通过有序二叉树来组织数据的,不过,TreeMap通过节点的链接来组织存储结构, 而PriorityQueue是通过数组的一些列计算确定逻辑上的树的节点的存放位置。