1. why data compression
-- To save space when storing it.
-- To save time when transmitting it.
-- Most files have lots of redundancy.
2. Lossless compression and expansion
-- Message: Binary data B we want to compress.
-- Compress: Generates a "compressed" representation C (B).
-- Expand: Reconstructs original bitstream B.
-- Compression ratio. Bits in C (B) / bits in B.
3. Fixed-length code: k-bit code supports alphabet of size 2^k
4. Reading and writing binary data
public class BinaryStdIn {
boolean readBoolean() {} //read 1 bit of data and return as a boolean value
char readChar() {} //read 8 bits of data and return as a char value
char readChar(int r) {} //read r bits of data and return as a char value
[similar methods for byte (8 bits); short (16 bits); int (32 bits); long and double (64 bits)]
boolean isEmpty() {} //is the bitstream empty?
void close() {} //close the bitstream
}
public class BinaryStdOut {
void write(boolean b) {} //write the specified bit
void write(char c) {} //write the specified 8-bit char
void write(char c, int r) {} //write the r least significant bits of the specified char
[similar methods for byte (8 bits); short (16 bits); int (32 bits); long and double (64 bits)]
void close() {} //close the bitstream
}
5. examine the contents of a bitstream:
6. Proposition. No algorithm can compress every bitstream.
Pf 1. [by contradiction]
-- Suppose you have a universal data compression algorithm U that can compress every bitstream.
-- Given bitstream B0, compress it to get smaller bitstream B1.
-- Compress B1 to get a smaller bitstream B2.
-- Continue until reaching bitstream of size 0.
-- Implication: all bitstreams can be compressed to 0 bits!
Pf 2. [by counting]
-- Suppose your algorithm that can compress all 1,000-bit streams.
-- 2^1000 possible bitstreams with 1,000 bits.
-- Only 1 + 2 + 4 + … + 2^998 + 2^999 < 2^1000 can be encoded with ≤ 999 bits. Similarly, only 1 in 2^499 bitstreams can be encoded with ≤ 500 bits!
7. Run-length encoding:
-- Simple type of redundancy in a bitstream: Long runs of repeated bits.
-- Representation: k-bit counts to represent alternating runs of 0s and 1s. If repeats longer than 2^k-1, intersperse runs of length 0.
-- Java implementation
public class RunLength
{
private final static int R = 256; //maximum run-length count
private final static int lgR = 8; //number of bits per count
public static void compress()
{
char repeats = 0;
boolean bit = false
while (!BinaryStdIn.isEmpty())
{
if ( BinaryStdIn.readBoolean() == bit ) {
repeats ++;
if ( repeats == R-1) {
repeats = 0;
bit = !bit;
BinaryStdout.write(repeats);
}
}
else {
repeats = 1;
bit = !bit;
BinaryStdout.write(repeats);
}
}
if ( repeats > 0 ) {
BinaryStdout.write(repeats);
}
}
public static void expand()
{
boolean bit = false;
while (!BinaryStdIn.isEmpty())
{
int run = BinaryStdIn.readInt(lgR); //read 8-bit count from standard input
for (int i = 0; i < run; i++)
BinaryStdOut.write(bit); //write 1 bit to standard output
bit = !bit;
}
BinaryStdOut.close(); //pad 0s for byte alignment
}
}
8. Avoid ambiguity: Ensure that no codeword is a prefix of another.
-- Fixed-length code.
-- Append special stop char to each codeword.
-- General prefix-free code.
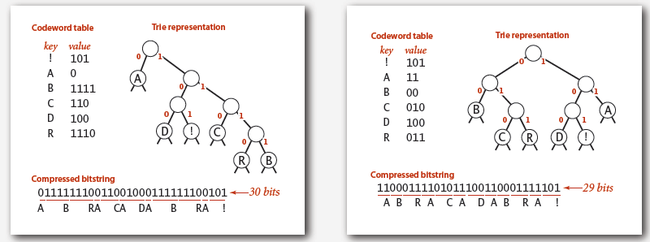
9. Prefix-free code:
-- Representation:
-- A binary trie.
-- Chars in leaves.
-- Codeword is path from root to leaf.
-- Compression:
-- Method 1: start at leaf; follow path up to the root; print bits in reverse.
-- Method 2: create ST of key-value pairs.
-- Expansion.
-- Start at root.
-- Go left if bit is 0; go right if 1.
-- If leaf node, print char and return to root.
private static class Node implements Comparable<Node>
{
private final char ch; // used only for leaf nodes
private final int freq; // used only for compress
private final Node left, right;
public Node(char ch, int freq, Node left, Node right)
{
this.ch = ch;
this.freq = freq;
this.left = left;
this.right = right;
}
public boolean isLeaf()
{ return left == null && right == null; }
public int compareTo(Node that)
{ return this.freq - that.freq; }
}
-- expansion implementation: performance linear in input size
public void expand()
{
Node root = readTrie(); //read in encoding trie
int N = BinaryStdIn.readInt(); //read in number of chars
for (int i = 0; i < N; i++)
{
Node x = root;
while (!x.isLeaf())
{
if (!BinaryStdIn.readBoolean())
x = x.left;
else
x = x.right;
}
BinaryStdOut.write(x.ch, 8);
}
BinaryStdOut.close();
}
-- transmit the trie
-- write: write preorder traversal of trie; mark leaf and internal nodes with a bit.
private static void writeTrie(Node x)
{
if (x.isLeaf())
{
BinaryStdOut.write(true);
BinaryStdOut.write(x.ch, 8);
return;
}
BinaryStdOut.write(false);
writeTrie(x.left);
writeTrie(x.right);
}
-- read: reconstruct from preorder traversal of trie.
private static Node readTrie()
{
if (BinaryStdIn.readBoolean())
{
char c = BinaryStdIn.readChar(8);
return new Node(c, 0, null, null);
}
Node x = readTrie();
Node y = readTrie();
return new Node('\0', 0, x, y);
}
10. Shannon-Fano algorithm ( top down ):
-- Partition symbols S into two subsets S0 and S1 of (roughly) equal freq.
-- Codewords for symbols in S0 start with 0; for symbols in S1 start with 1.
-- Recur in S0 and S1.
-- not optimal
11. Huffman algorithm ( bottom up ):
-- Count frequency freq[i] for each char i in input.
-- Start with one node corresponding to each char i (with weight freq[i]).
-- Repeat until single trie formed:
-- select two tries with min weight freq[i] and freq[j]
-- merge into single trie with weight freq[i] + freq[j]
-- Java Implementaton:
private static Node buildTrie(int[] freq)
{
MinPQ<Node> pq = new MinPQ<Node>();
for (char i = 0; i < R; i++)
if (freq[i] > 0)
pq.insert(new Node(i, freq[i], null, null));
while (pq.size() > 1)
{
Node x = pq.delMin();
Node y = pq.delMin();
Node parent = new Node('\0', x.freq + y.freq, x, y);
pq.insert(parent);
}
return pq.delMin();
}
-- Encoding:
-- Pass 1: tabulate char frequencies and build trie.
-- Pass 2: encode file by traversing trie or lookup table.
-- Running time: N + R log R .
12. Different compression modules:
-- Static model. Same model for all texts.
- Fast.( no pre-scan, no model transmit )
- Not optimal: different texts have different statistical properties.
- Ex: ASCII, Morse code.
-- Dynamic model. Generate model based on text.
- Preliminary pass needed to generate model.
- Must transmit the model.
- Ex: Huffman code.
-- Adaptive model. Progressively learn and update model as you read text.
- More accurate modeling produces better compression.
- Decoding must start from beginning.
- Ex: LZW.
13. Lempel-Ziv-Welch compression:
-- Create ST associating W-bit codewords with string keys.
-- Initialize ST with codewords for single-char keys.
-- Find longest string s in ST that is a prefix of unscanned part of input.
-- Write the W-bit codeword associated with s.
-- Add s + c to ST, where c is next char in the input.
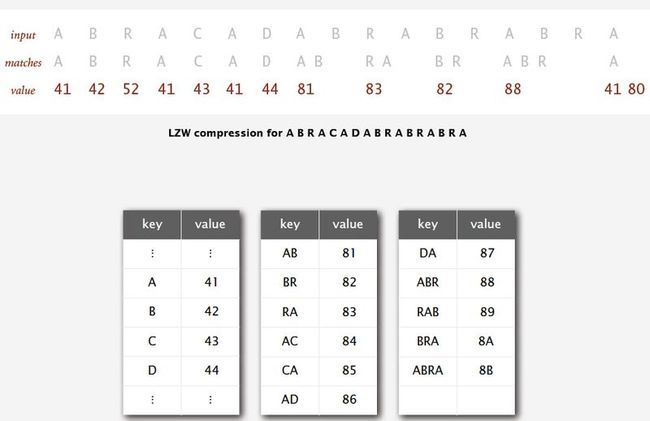
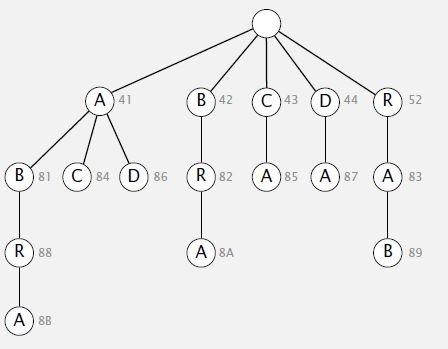
-- Representation of LZW compression code table: A trie to support longest prefix match.
-- Java Implementatin of compression:
public static void compress()
{
String input = BinaryStdIn.readString();
TST<Integer> st = new TST<Integer>();
//codewords for singlechar, radix R keys
for (int i = 0; i < R; i++)
st.put("" + (char) i, i);
int code = R+1;
while (input.length() > 0)
{
//find longest prefix match s
String s = st.longestPrefixOf(input);
//write W-bit codeword for s
BinaryStdOut.write(st.get(s), W);
int t = s.length();
//L = 2^W - 1, the max codes
if (t < input.length() && code < L)
st.put(input.substring(0, t+1), code++);
input = input.substring(t);
}
//write "stop" codeword and close output stream
BinaryStdOut.write(R, W);
BinaryStdOut.close();
}
-- LZW expansion
-- Create ST associating string values with W-bit keys.
-- Initialize ST to contain single-char values.
-- Read a W-bit key.
-- Find associated string value in ST and write it out.
-- Update ST.
-- Representation of expansion code table : An array of size 2^W.
-- tricky case:
14. Data compression summary
-- Lossless compression.
- Represent fixed-length symbols with variable-length codes. [Huffman]
- Represent variable-length symbols with fixed-length codes. [LZW]
-- Theoretical limits on compression. Shannon entropy: H(X) = - Sum ( i ) { p(xi) lg p(xi) }