1. Quicksort is honored as one of top 10 algorithms of 20th century in science and engineering. It's prevalent in practice, takes O(nlogn) time "on average" and works in place.
2. Partition around a pivot :
a) pick an element of the array
b) rearrage the array so that:
- those elements left to pivot are less than pivot
- those elements right to pivot are greater than pivot
result : the pivot is put in its "rightful position"
cool facts: linear (O(n)) time, no extra memory & it reduces problem size
3. Quick Sort High-Level Description: QuickSort(array A, length n)
a) if n=1, return
b) p = choosePivot(A, n)
c) partition A around p
d) recursively sort 1st part
e) recursively sort 2nd part
4. Algorithm of partition:
1) The easy way out is to scan the array put all those elements greater than pivot to the right most available position of a new array and all those elements less than pivot to the left most available position of the new array.
2) In-Place Implementation :
a) pivot = the 1st element of the array ( if not, just swap the pivot with the 1st element)
b) maintain the following invariant :
5. In-Place Partition Algorithm: Partition( A, l, r) ( input = A[l...r] )
a) p = A[l];
b) i = l + 1;
c) for j = l + 1 to r :
if ( A[j] < p )
-- swap A[i] and A[j]
-- i ++
d) swap A[l] and A[i -1]
e) return i-1
Running Time is O(n) , where n = r-l + 1 is the length of the subarray.
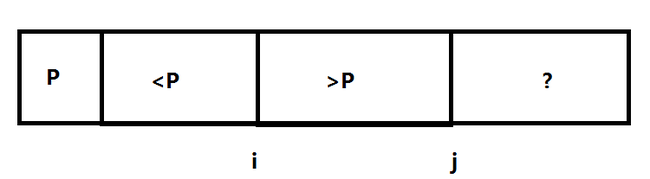
Correctness : the loop maintain the invariant :
a) A[l+1], ... , A[i-1] are all less than pivot
b) A[i] , ... , A[j-1] are all greater than pivot
c) A[j] is not checked
6. Induction Review :
Let P(n) = Assertion parameterized by positive integer n.
To prove P(n) for all n>= 1 by induction:
a) base case : directly prove that P(1) holds
b) inductive step: for every n >=2, prove that : if P(k) holds for all k<n , then P(n) holds as well.
7. Correctness of Quick Sort:
P(n) = "Quick Sort correctly sorts every input array of length n for every n >=1".
Proof by induction:
a) base case : every input array of length 1 is already sorted. Quick Sort returns the input array, which is correct. (P(1) holds)
b) inductive step : Fix n >= 2, Fix some input array A of length n , if P(k) holds for any k < n:
because pivot winds up in correct position, the pivot is greater than left subarray and less than right subarray. while the sizes of left subarray and right subarray are less than n, by induction afer recursive calls , they are sorted. So the entire array of length n is sorted.