深度学习-数据操作

数据操作

首先，我们来介绍n维数组，也称为张量（tensor）。GPU很好地支持加速计算，而NumPy仅支持CPU计算；并且张量类支持自动微分。 这些功能使得张量类更适合深度学习。

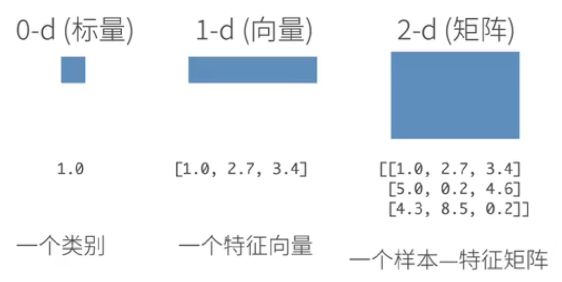
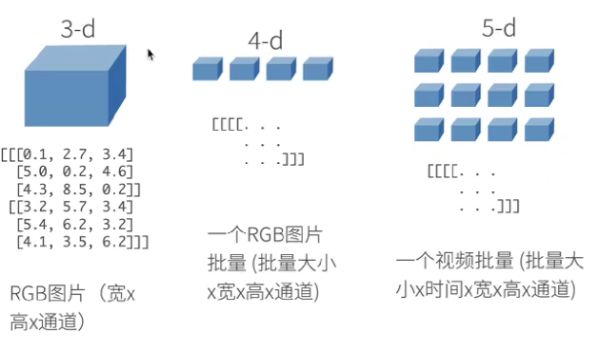
张量表示一个由数值组成的数组，这个数组可能有多个维度。 具有一个轴的张量对应数学上的向量（vector）； 具有两个轴的张量对应数学上的矩阵（matrix）； 具有两个轴以上的张量没有特殊的数学名称。

上图分别是1维到5维的张量的表示情况

1. 基础张量方法

可以使用arange 创建一个行向量 x。这个行向量包含以0开始的前12个整数，它们默认创建为整数：

输入：x = torch.arange(12)
输出：tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

可以通过张量的shape属性来访问张量（沿每个轴的长度）的形状：

输入：x.shape
输出：torch.Size([12])

要想改变一个张量的形状而不改变元素数量和元素值，可以调用reshape函数：

输入：X = x.reshape(3, 4)，并且输出X
输出：tensor([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]])

我们可以通过-1来调用此自动计算出维度的功能。 即对于原来12个元素的张量，我们可以用：

x.reshape(-1,4) 或 x.reshape(3,-1) 来取代 x.reshape(3,4)。

此外还有：

# 全零张量
torch.zeros((2, 3, 4))
tensor([[[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]],
        [[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]]])

# 全1张量
torch.ones((2, 3, 4))
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],
        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])

# 随机张量，其中的每个元素都从均值为0、标准差为1的标准高斯分布（正态分布）中随机采样
torch.randn(3, 4)
tensor([[-0.0135,  0.0665,  0.0912,  0.3212],
        [ 1.4653,  0.1843, -1.6995, -0.3036],
        [ 1.7646,  1.0450,  0.2457, -0.7732]])

# 手动输入张量
torch.tensor([[2, 1, 4, 3], 
              [1, 2, 3, 4], 
              [4, 3, 2, 1]])
tensor([[2, 1, 4, 3],
        [1, 2, 3, 4],
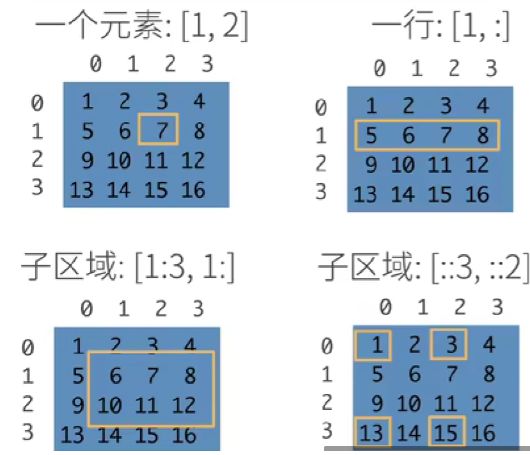
        [4, 3, 2, 1]])

如上图所示，可以用冒号代表全部取出的意思。

其中的"：：3"表示隔着3行，"：：2"隔着2列取出。

2. 运算符

x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y  # **运算符是求幂运算

tensor([ 3.,  4.,  6., 10.]),
tensor([-1.,  0.,  2.,  6.]),
tensor([ 2.,  4.,  8., 16.]),
tensor([0.5000, 1.0000, 2.0000, 4.0000]),tensor([ 1.,  4., 16., 64.])

也可以把多个张量连结（concatenate）在一起， 把它们端对端地叠起来形成一个更大的张量。

下面的例子分别演示了当我们沿行（轴-0，形状的第一个元素） 和按列（轴-1，形状的第二个元素）连结两个矩阵时，会发生什么情况。

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0) # 按行连接，可以理解为堆起来
torch.cat((X, Y), dim=1) # 按列连接，可以理解为靠一起

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.],
        [ 2.,  1.,  4.,  3.],
        [ 1.,  2.,  3.,  4.],
        [ 4.,  3.,  2.,  1.]]),
 
tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],
        [ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],
        [ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]])

3. 广播机制

在某些情况下，即使形状不同【但是要求维度相同】，我们仍然可以通过调用 广播机制（broadcasting mechanism）来执行按元素操作。

当两个张量形状不一致时，能否进行广播，有以下规则：

  从尾部维度向前逐一比较维度数：

1. 如果维度相等，✅ 可以广播

2. 如果其中一个是 1，✅ 可以广播（扩展成另一个维度大小）

3. 否则 ❌ 无法广播

  这种机制的工作方式如下：

1. 通过适当复制元素来扩展一个或两个数组，以便在转换之后，两个张量具有相同的形状；

2. 对生成的数组执行按元素操作。

a = torch.tensor([[0],
                  [1],
                  [2]])
b = torch.tensor([[0, 1]])
# 其中：a维度为（3,1），b维度为（1,2），比较尾数中a含1，可以进行广播机制输出
a + b = torch.tensor([[0, 1],[1, 2],[2, 3]])

4. 索引与切片

张量中的元素可以通过索引访问：第一个元素的索引是0，最后一个元素索引是-1；可以指定范围以包含第一个元素和最后一个之前的元素。

例如：

• 我们可以用 [-1] 选择最后一个元素；

• 可以用 [1:3] 选择第二个和第三个元素；

• 可以用 [0:2, :] 访问第1行和第2行，其中 “:” 代表沿轴1（列）的所有元素。

[a:b]表示选择了第a行到第b-1行的元素，即：左闭右开[a,b)。

5. 节省内存（原地操作）

运行一些操作可能会导致为新结果分配内存。

例如，如果我们用Y = X + Y，我们将取消引用Y指向的张量，而是指向新分配的内存处的张量。通过Python的id()函数（查找地址），我们可以看到：

before = id(Y)
Y = Y + X
id(Y) == before

结果为：False，说明Y执行操作后被重新分配了地址。

这可能是不可取的，原因有两个：

1. 我们不想总是不必要地分配内存。在机器学习中，我们可能有数百兆的参数，并且会多次更新所有参数。通常情况下，我们希望原地执行这些更新；

2. 如果我们不原地更新，其他引用仍然会指向旧的内存位置，这样某些代码可能会无意中引用旧的参数。

幸运的是，执行原地操作非常简单。

我们可以使用切片表示法将操作的结果分配给先前分配的数组：

Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))

结果为：
id(Z): 140327634811696
id(Z): 140327634811696

注意：如果在后续计算中没有重复使用X， 我们也可以使用 X[:] = X + Y 或 X += Y 来减少操作的内存开销。

6. 转为其他对象

torch张量和numpy数组转换：

A = X.numpy()
B = torch.tensor(A)
type(A), type(B)

结果为：
numpy.ndarray,torch.Tensor

大小为1的张量转换为Python标量： 

a = torch.tensor([3.5])
a, a.item(), float(a), int(a)


结果为：
tensor([3.5000]), 3.5, 3.5, 3

数据预处理

1. 读取数据集

import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')  # 列名
    # 每行表示一个数据样本
    f.write('NA,Pave,127500\n')      
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

import pandas as pd
data = pd.read_csv(data_file)
print(data)

结果为：
    NumRooms Alley   Price
0     NaN    Pave    127500
1     2.0    NaN     106000
2     4.0    NaN     178100
3     NaN    NaN     140000

2. 处理缺失项

通过位置索引iloc，我们将data分成inputs和outputs， 其中前者为data的前两列，而后者为data的最后一列。

对于inputs中缺少的数值，我们用同一列的均值替换“NaN”项。【插值法】

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs = inputs.fillna(inputs.mean())
# inputs.mean()为3，fillna操作把缺失值填补为3
print(inputs)

结果为：
    NumRooms Alley 
0     3.0    Pave 
1     2.0    NaN 
2     4.0    NaN  
3     3.0    NaN  

对于inputs中的类别值或离散值，我们将“NaN”视为一个类别。 由于“巷子类型”（“Alley”）列只接受两种类型的类别值“Pave”和“NaN”， pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。

巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1，“Alley_nan”的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。

inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)

结果为：
    NumRooms Alley_pave   Alley_nan
0     3.0        1            0
1     2.0        0            1
2     4.0        0            1
3     3.0        0            1

3. 转为张量

import torch
X = torch.tensor(inputs.to_numpy(dtype=float))
y = torch.tensor(outputs.to_numpy(dtype=float))
X, y

结果为：
tensor([[3., 1., 0.],
        [2., 0., 1.],
        [4., 0., 1.],
        [3., 0., 1.]], dtype=torch.float64),
tensor([127500., 106000., 178100., 140000.], dtype=torch.float64)