学习笔记(33):matplotlib绘制简单图表-绘制混淆矩阵热图
学习笔记(33):matplotlib绘制简单图表-绘制混淆矩阵热图
一、绘制混淆矩阵热图代码解析
1.1、导入必要的库
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
import seaborn as sns
matplotlib.pyplot:Python 中最常用的绘图库,用于创建各种图表confusion_matrix:来自 scikit-learn 库,专门用于计算分类模型的混淆矩阵seaborn:基于 matplotlib 的高级可视化库,提供更美观的默认图表样式
2.2、准备示例数据
y_true = [0, 1, 0, 1, 1] # 真实标签
y_pred = [0, 1, 1, 1, 0] # 模型预测标签
这是两组简单的分类标签数据,用于演示混淆矩阵的计算。其中:
- 真实标签包含 3 个正例 (1) 和 2 个负例 (0)
- 预测标签包含 2 个正例和 3 个负例
1.3、计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)
confusion_matrix 函数计算出的混淆矩阵是一个二维数组,其结构为:
[[TN, FP],
[FN, TP]]
对于示例数据,计算得到的混淆矩阵为:
[[1, 1],
[1, 2]]
- 左上角 (1):真负例 (TN) - 真实为负且预测为负
- 右上角 (1):假正例 (FP) - 真实为负但预测为正
- 左下角 (1):假负例 (FN) - 真实为正但预测为负
- 右下角 (2):真正例 (TP) - 真实为正且预测为正
1.4、使用 seaborn 绘制热图
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
heatmap():seaborn 中用于绘制热力图的函数
annot=True:在每个单元格中显示数值
fmt='d':指定数值格式为整数
cmap='Blues':使用蓝色系的配色方案
1.5、设置图表标签和标题,展示图
plt.xlabel('Predicted') # x轴标签:预测类别
plt.ylabel('True') # y轴标签:真实类别
plt.title('Confusion Matrix') # 图表标题plt.show()
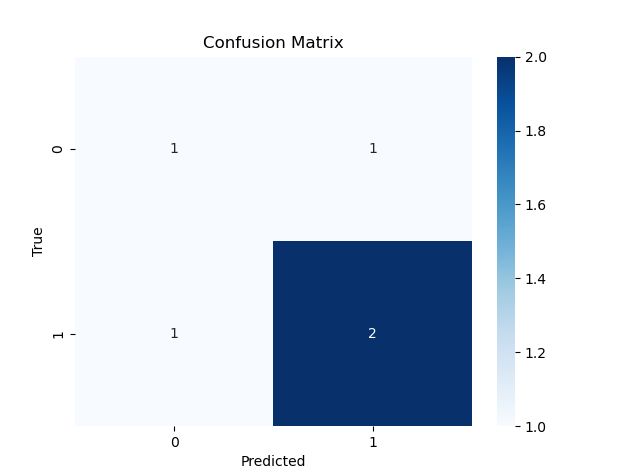
最终生成的混淆矩阵热图直观展示了模型在分类任务中的表现:
- 对角线单元格 (TN 和 TP) 表示预测正确的样本数
- 非对角线单元格 (FP 和 FN) 表示预测错误的样本数
这个可视化工具常用于评估分类模型的性能,特别是在处理不平衡数据集时非常有用。
二、代码和执行结果
2.1、代码
import matplotlib.pyplot as plt
# 示例:绘制混淆矩阵热图
from sklearn.metrics import confusion_matrix
import seaborn as sns
y_true = [0, 1, 0, 1, 1]
y_pred = [0, 1, 1, 1, 0]
cm = confusion_matrix(y_true, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('Predicted')
plt.ylabel('True')
plt.title('Confusion Matrix')
plt.show()2.2、执行结果
三、如何计算混淆矩阵
混淆矩阵的计算核心是统计 “真实标签” 与 “预测标签” 的所有组合情况
3.1、数据
y_true = [0, 1, 0, 1, 1] # 真实标签:[0,1,0,1,1]
y_pred = [0, 1, 1, 1, 0] # 预测标签:[0,1,1,1,0]
- 真实标签
y_true = [0, 1, 0, 1, 1](共 5 个样本,0 和 1 为两类) - 预测标签
y_pred = [0, 1, 1, 1, 0](模型对每个样本的预测结果)
3.2、计算步骤
步骤 1:明确混淆矩阵的维度和指标
二分类问题的混淆矩阵是2×2 矩阵,行代表 “真实标签”,列代表 “预测标签”,包含 4 个核心指标:
| 真实标签 \ 预测标签 | 预测为 0(负类) | 预测为 1(正类) |
|---|---|---|
| 真实为 0(负类) | TN(真负例) | FP(假正例) |
| 真实为 1(正类) | FN(假负例) | TP(真正例) |
- TN:真实是 0,预测也是 0(正确预测负类)
- FP:真实是 0,预测是 1(错误预测为正类)
- FN:真实是 1,预测是 0(错误预测为负类)
- TP:真实是 1,预测也是 1(正确预测正类)
步骤 2:逐样本匹配,统计四类指标
将每个样本的 “真实标签” 和 “预测标签” 一一对应,判断属于哪类指标:
| 样本序号 | 真实标签 | 预测标签 | 对应指标 |
|---|---|---|---|
| 1 | 0 | 0 | TN |
| 2 | 1 | 1 | TP |
| 3 | 0 | 1 | FP |
| 4 | 1 | 1 | TP |
| 5 | 1 | 0 | FN |
统计每个指标的数量:
- TN:1 个(样本 1)
- FP:1 个(样本 3)
- FN:1 个(样本 5)
- TP:2 个(样本 2、样本 4)
步骤 3:构建混淆矩阵
按 “真实标签行 × 预测标签列” 的顺序,将统计结果填入矩阵:
# 第一行(真实为0):TN=1,FP=1
# 第二行(真实为1):FN=1,TP=2混淆矩阵 = [[1, 1], # 真实0对应的预测结果
[1, 2]] # 真实1对应的预测结果
结果验证:代码验证
运行sklearn的confusion_matrix函数,结果完全一致:
from sklearn.metrics import confusion_matrix
y_true = [0, 1, 0, 1, 1]
y_pred = [0, 1, 1, 1, 0]
print(confusion_matrix(y_true, y_pred))
输出结果:
[[1 1]
[1 2]]
总结
计算混淆矩阵的关键是:
- 明确 “真实标签” 和 “预测标签” 的类别(如 0 和 1);
- 逐样本判断属于 TN/FP/FN/TP 中的哪一类;
- 统计每类的数量,按 “真实行 × 预测列” 填入矩阵。
通过混淆矩阵可以直观看到模型的错误类型(如 FP 多说明容易误判负类为正类),是评估分类模型的基础工具。