算法训练day22|二叉树part08(LeetCode235. 二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点)

235. 二叉搜索树的最近公共祖先

题目链接
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

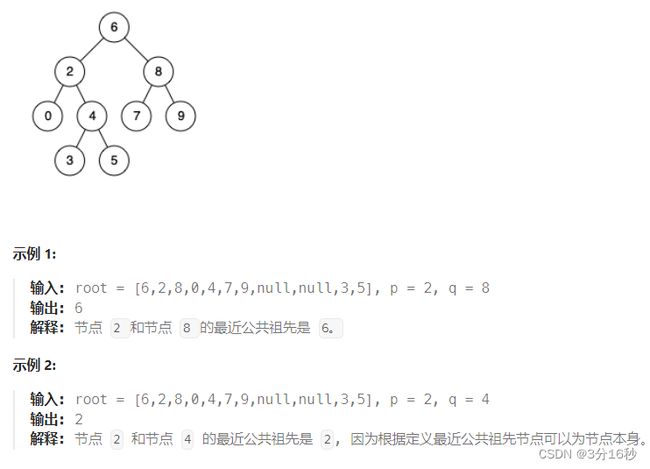
说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

思路分析

那么本题是二叉搜索树，二叉搜索树是有序的，那得好好利用一下这个特点。

在有序树里，如何判断一个节点的左子树里有p，右子树里有q呢？

因为是有序树，所有 如果 中间节点是 q 和 p 的公共祖先，那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。

那么只要从上到下去遍历，遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是q 和 p的公共祖先。 那问题来了，一定是最近公共祖先吗？

如图，我们从根节点搜索，第一次遇到 cur节点是数值在[p, q]区间中，即 节点5，此时可以说明 p 和 q 一定分别存在于 节点 5的左子树，和右子树中。

此时节点5是不是最近公共祖先？ 如果 从节点5继续向左遍历，那么将错过成为q的祖先， 如果从节点5继续向右遍历则错过成为p的祖先。

所以当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[p, q]区间中，那么cur就是 p和q的最近公共祖先。

理解这一点，本题就很好解了。

而递归遍历顺序，本题就不涉及到 前中后序了（这里没有中节点的处理逻辑，遍历顺序无所谓了）。

如图所示：p为节点6，q为节点9

可以看出直接按照指定的方向，就可以找到节点8，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！

递归法

递归三部曲如下：

1.确定递归函数返回值以及参数

参数就是当前节点，以及两个结点 p、q。
返回值是要返回最近公共祖先，所以是TreeNode * 。

TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q)

2.确定终止条件

遇到空返回就可以了，代码如下：

if (cur == NULL) return cur;

其实都不需要这个终止条件，因为题目中说了p、q 为不同节点且均存在于给定的二叉搜索树中。也就是说一定会找到公共祖先的，所以并不存在遇到空的情况。
3. 确定单层递归的逻辑

在遍历二叉搜索树的时候就是寻找区间[p->val, q->val]（注意这里是左闭又闭）
那么如果 cur->val 大于 p->val，同时 cur->val 大于q->val，那么就应该向左遍历（说明目标区间在左子树上）。
需要注意的是此时不知道p和q谁大，所以两个都要判断

if (cur->val > p->val && cur->val > q->val) {
   
    TreeNode* left = traversal(cur->left, p, q);
    if (left != NULL) {
   
        return left;
    }
}

在这里调用递归函数的地方，把递归函数的返回值left，直接return。
如果 cur->val 小于 p->val，同时 cur->val 小于 q->val，那么就应该向右遍历（目标区间在右子树）。

if (cur->val < p->val && cur->val < q->val) {
   
    TreeNode* right = traversal(cur->right, p, q);
    if (right != NULL) {
   
        return right;
    }
}

剩下的情况，就是cur节点在区间（p->val <= cur->val && cur->val <= q->val）或者 （q->val <= cur->val && cur->val <= p->val）中，那么cur就是最近公共祖先了，直接返回cur。

return cur;

要搜索一条边，还是搜索整个树呢？

在路径总和中说了 递归函数有返回值就是要遍历某一条边，但有返回值也要看如何处理返回值！
如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？
搜索一条边的写法：

if (递归函数(root->left)) return ;

if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);  // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理;         // 中 

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

本题就是标准的搜索一条边的写法，遇到递归函数的返回值，如果不为空，立刻返回。

完整代码：

class Solution {
   
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
   
        TreeNode* cur=root;
        if(cur==NULL) return NULL;
        if(cur->val>p->val&&cur->val>q->val){
   
            TreeNode* left=lowestCommonAncestor(cur->left,p,q);
            return left;
        }
        else if(cur->val<p->val&&cur->val<q->val){
   
            TreeNode*