葡萄学习——C语言必备(一)
各种进制转换
一、进制的基本概念(到底什么是进制)
1.进制(基数):表示数时所用的数字符号的个数。
比如:
-
十进制:基数10,用
0~9表示(就是我们常用的数字) -
二进制:基数2,用
0~1表示 -
八进制:基数8,用
0~7表示 -
十六进制:基数16,用
0~9, A(10), B(11), C(12), D(13), E(14), F(15)表示
小技巧:可以简单理解为基数不同(基数是几,就是几进制)
2.权值:每一位数字代表的实际值。例如十进制数 253:
-
2 的权值是
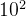 =100 → 2×100=200 →2×
=100 → 2×100=200 →2×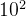
-
5 的权值是
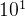 =10 → 5×10=50 → 5×
=10 → 5×10=50 → 5×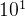
-
3 的权值是
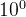 =1 → 3×1=3 → 3×
=1 → 3×1=3 → 3×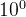
-
总和:200+50+3=253(2×
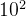 + 5×
+ 5×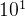 + 3×
+ 3×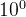 =253)
=253)
小技巧:可以简单理解为这个位数上是几(数字是几,权值就是几)
公式:
二、十进制 → 其他进制
1. 十进制 → 二进制(重点!)
方法:除2取余法(倒序排列余数)
例子:将十进制数 25 转换为二进制(注意:第一个余数是最低位)
步骤:
25 ÷ 2 = 12 余 1 → 最低位
12 ÷ 2 = 6 余 0
6 ÷ 2 = 3 余 0
3 ÷ 2 = 1 余 1
1 ÷ 2 = 0 余 1 → 最高位结果:余数倒序排列 → 11001,即 25(十进制)=11001(二进制)
2. 十进制 → 八进制/十六进制
方法:除基取余法(基数为8或16)
例子:将十进制数 100 转换为八进制和十六进制
八进制:
100 ÷ 8 = 12 余 4 → 最低位
12 ÷ 8 = 1 余 4
1 ÷ 8 = 0 余 1 → 最高位
十六进制:
100 ÷ 16 = 6 余 4 → 最低位
6 ÷ 16 = 0 余 6 → 最高位
结果:余数倒序 → 64 → \(100_{10} = 64_{16}\)结果:余数倒序排列 → 144 ,即100(十进制)=144(八进制)
结果:余数倒序排列 → 64 ,即100(十进制)=64(十六进制)
其实十进制转换其他进制都是除基取余法
三、其他进制 → 十进制
方法:按权展开求和
公式:每一位数字×基数^位置(从右往左,位置从0开始)
1. 二进制 → 十进制
例子:将 11001(二进制)转换为十进制
权值展开:
1×2^0+ 0×2^1+ 0×2^2 + 1×2^3 + 1×2^4
= 16 + 8 + 0 + 0 + 1 = 25
结果:25,即 11001(二进制)= 25(十进制)
2. 八进制 → 十进制
例子:将 144(八进制)转换为十进制
权值展开:
4×8^0+1×8^2+4×8^1
= 4 + 32 + 64= 100
结果:100,即 144(八进制)= 100(十进制)
3. 十六进制 → 十进制
例子:将 2A(十六进制) 转换为十进制
权值展开:
10×16^0 + 2×16^1(A代表10)
= 10 + 32 = 42结果:42,即 2A(十六进制)= 42(十进制)
四、二进制 ↔ 八进制/十六进制
(其实不好理解不看第四部分也行,记住其他进制转十进制和十进制转其他进制即可,可以转换两次就行,但是记得看最后的总结呦)例如,要将二进制转换为八进制,可以先将二进制转为十进制,然后再将十进制转为八进制。这种方法虽然可行,但可能效率较低,尤其是在处理较大的数字时。
1. 二进制 ↔ 八进制
(1)二进制 → 八进制
每3位二进制为一组,转换为1位八进制(不足补0)
例子:11001(二进制) → 补0即为 011 001
011 → 1×2^0 + 1×2^1 + 1×2^2 = 1×1 + 1×2 + 0×4 = 3
001 → 1×2^0 + 0×2^1 + 0×2^2 = 1×1 + 0×2 + 0×4 = 1结果:31,即 11001(二进制)= 31(八进制)
(2)八进制 → 二进制
每位八进制展开为3位二进制
例子:将31(八进制) 转换为二进制
3 → 查表得 011(因为 3=1×1+1×2+0×4)
1 → 查表得 001(因为 1=1×1+0×2+0×4)结果:拼接后的二进制:011(来自3) + 001(来自1) = 011001,去掉前导零(开头的零)011001 → 去掉前面的0 → 11001
八二进制对照表:
| 八进制 | 二进制(3位) |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
ps.
i.为什么每个八进制数字要转成3位二进制?
核心原因:八进制基数是8,而![]() ,所以每个八进制数字对应 3位二进制。(其它进制转换同理)
,所以每个八进制数字对应 3位二进制。(其它进制转换同理)
ii.为什么中间要补零?
补零到3位是为了保证每个八进制数字对应的二进制位数足够。
-
例子:八进制的
5→ 直接转二进制是101(已经是3位,不用补零)。 八进制的2→ 转二进制是10,但需要补零到3位 →010
iii.错误示范(如果不补零会怎样?)
假设不补零:
3 → 二进制 11(只有2位)
1 → 二进制 1(只有1位)
拼接后:111 → 这是 7(八进制),和原数 31(八进制) 完全不同!
结论:必须补零到3位,否则会丢失数值信息!
2. 二进制 ↔ 十六进制
(1)二进制 → 十六进制
每4位二进制为一组,转换为1位十六进制(不足补0)
例子:将11001(二进制)转十六进制
0001 → 1
1001 → 8 + 0 + 0 + 1 = 9结果: 补0为 0001 1001 → 19(十六进制)
(2) 十六进制 → 二进制
每位十六进制展开为4位二进制
例子:将19(十六进制) 转换为二进制
1 → 查表得 0001(因为 1=0×8+0×4+0×2+1×1)
9 → 查表得 1001(因为 9=1×8+0×4+0×2+1×1)结果:将所有二进制片段拼接0001(来自1) + 1001(来自9) = 00011001,去掉前导零(开头的零)00011001 → 去掉前面的0 → 11001
十六二进制对照表:
| 十六进制 | 二进制(4位) |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A (10) | 1010 |
| B (11) | 1011 |
| C (12) | 1100 |
| D (13) | 1101 |
| E (14) | 1110 |
| F (15) | 1111 |
ps.
i.为什么每个八进制数字要转成4位二进制?
核心原因:十六进制基数是16,而![]() ,所以每个十六进制数字对应43位二进制。(其它进制转换同理)
,所以每个十六进制数字对应43位二进制。(其它进制转换同理)
ii.为什么中间要补零?
补零到4位是为了保证每个八进制数字对应的二进制位数足够。
-
例子:十六进制的
5→ 直接转二进制是0101(已经是4位)。 十六进制的2→ 转二进制是0010(不足4位需补零)
iii.错误示范(如果不补零会怎样?)
假设不补零:
1 → 二进制 1(只有1位)
9 → 二进制 1001(4位)
拼接后:11001 → 这是 19(十六进制)吗?
看似正确,但这是巧合!如果换成其他数字,比如 A(十六进制) → 1010(二进制),若省略前导零,直接写 1010 是正确的,但若中间有拼接时可能会出错。
结论:必须统一补零到4位,否则拼接时会错位!
五、八进制 ↔ 十六进制
先转二进制,再转目标进制。
例子:将 31(八进制)转换为十六进制
八进制 → 二进制:3 → 011, 1 → 001 → 011001(二进制)
二进制 → 十六进制:补0为 0001 1001 → 19(十六进制)为什么八进制转十六进制需要二进制中转?
-
根本原因:八进制和十六进制没有直接的数学关系,但都和二进制有天然联系:
-
1位八进制 = 3位二进制(因为 8=238=23)
-
1位十六进制 = 4位二进制(因为 16=2416=24)
-
-
中转优势:通过二进制可以避免直接转换的复杂计算。
八进制 → 二进制 → 补零到4位倍数 → 分组转十六进制
六、总结表(快速记忆)
| 转换类型 | 方法 | 例子 |
|---|---|---|
| 十进制 → 其他进制 | 除基取余,倒序排列 | 25 → 11001(二进制) |
| 其他进制 → 十进制 | 按权展开求和 | 11001 → 25 |
| 二进制 ↔ 八进制 | 3位一组,补0分组 | 11001 → 31(八进制) |
| 二进制 ↔ 十六进制 | 4位一组,补0分组 | 11001 → 19(十六进制) |
| 八进制 ↔ 十六进制 | 二进制中转 | 31(八进制)→ 19(十六进制) |
七、常见误区
-
忘记补零:如二进制转八进制时,左侧不足3位要补0(如
11001补为011001)。 -
权值位置错误:权值从右往左,位置从0开始计算(最右边是第0位)。
-
进制符号混淆:十六进制的
A-F对应十进制的10-15,不要用字母以外的符号。
八、练习题(答案可自己验证)
-
将十进制数
47转换为二进制和八进制。 -
将二进制数
101101(二进制)转换为十进制和十六进制。 -
将十六进制数
3F(十六进制)转换为二进制和八进制。