C++中数学相关知识与例题（初级）

一、大小

关于几个数的大小，我们怎么比较它们的大小呢？

int a ,b;
cin>>a>>b;
if(a>=b) cout<<a;
else cout<<b;

最简单的，使用条件语句。
当然还可以这样

#include
using namespace std;
int main(){
	int a,b;
	cin>>a>>b;
    int z= a >= b ? a : b;
    cout<<z;
	return 0;
}

三目运算符

基本形式 ： <表达式1> ? <表达式2> : <表达式3>

很容易理解：看表达式1是否为真，如果为真，执行表达式2，否则执行表达式3.
或者这样

int a,b;
cin>>a>>b;
int maxx=max(a,b);
int minn=min(a,b);

在此基础上，你可以玩出花来了

二、最小公倍数&最大公约数

最小公倍数的定义:

几个数公有的倍数叫做这几个数的公倍数，其中最小的一个叫做这几个数的最小公倍数。

例如，4 的倍数有 4、8、12、16、20、24…，6 的倍数有 6、12、18、24、30…，12、24 等是 4 和 6 的公倍数，其中 12 是 4 和 6 的最小公倍数。

最大公约数的定义：

最大公约数，也称最大公因数，指两个或多个整数共有约数中最大的一个。例如，12 和 18，12 的约数有 1、2、3、4、6、12，18 的约数有 1、2、3、6、9、18，它们的公约数有 1、2、3、6，其中最大的是 6，所以 12 和 18 的最大公约数是 6。

关于求最大公约数我们一般使用辗转相除法即可，即用较大数除以较小数，再用出现的余数（第一余数）去除除数，再用出现的余数（第二余数）去除第一余数，如此反复，直到最后余数是 0 为止。此时的除数就是最大公约数。例如求 102 和 68 的最大公约数，102÷68 = 1……34，68÷34 = 2……0，所以 34 就是 102 和 68 的最大公约数。

至于最小公倍数，两数相乘再除以最大公约数即可。

定义很容易理解，直接上代码

#include
using namespace std;
const int N=1e6+10;
typedef long long ll;
int main(){
	int m,n;
	cin>>m>>n;
	int a=m,b=n;
	int r=m%n;
	while(r){//非0即为真，可以写为r！=0
		m=n;
		n=r;
		r=m%n;
	}
	cout<<"最大公约数"<<n<<endl;
	cout<<"最小公倍数"<<a*b/n<<endl;
    return 0;
}

除外我们还可以这样

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
ll gcd(ll m,ll n)
{
	if(n==m) return m;
	if(n>m) return gcd(n,m);
	if(m&1==0){
		if(n&1==0){
			return 2*gcd(m/2,n/2);
		}else return gcd(m/2,n);
	}else{
		if(n&1==0){
			return gcd(m,n/2);
		}else{
			return gcd(n,m-n);
		}
	}
}
int main(){
	ll n,m;
	cin>>n>>m;
	ll c=gcd(m,n);
	cout<<c<<" "<<n*m/c;//注意n*m可能超出int类型的范围
	return 0;
}

加减乘除

这个很基础：

#include
using namespace std;
int main(){
	int a,b;
	cin>>a>>b;
	cout<<a+b<<"\n";
    cout<<a-b<<"\n";
    cout<<a*b<<"\n";
    cout<<a/b<<"\n";
	return 0;
} 

但是我们要知道，数据类型是有长度的，如果一个数据有10000位，我们就算使用unsighed long long也无济于事，这时候就轮到**高精度**登场了

使用之前我们要先知道代替数据类型，即如何存储数据——答案就是使用数组存储

接下来是读入高精度

void read(int a[]){
	intlen,i;
	string s;
	cin>>s;
	len=s.length();
	memset(a,0,sizeof(a));
	for(int i=1;i<=len;i++) a[i]=s[len-i]-'0';
	a[0]=len;
}

接下来就是正菜了：

高精加

高精减

高精乘

高精减

进制

进制定义：

指进位制，是人们规定的一种进位方式表示某一位置上的数，运算时是逢X进一位。 比如十进制是逢十进一，二进制是逢二进一，八进制是逢八进一

取十进制转化为二进制为例：将某个十进制数除2得到的整数部分保留，作为第二次除2时的被除数，得到的余数依次记下，重复上述步骤，直到整数部分为0就结束，将所有得到的余数最终**逆序输出**，则为该十进制对应的二进制数。其他进制转化类似

#include
using namespace std;
const string R="0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";
//存储进制所对应的符号
int x;
void tox(int n){
	if(n/x==0){//边界
	cout<<R[n];
	return;
	}
	tox(n/x);//先递归 125/2=62
	cout<<R[n%x];//后输出 ,即倒序输出。 
}
int main(){
    int n;
    cin>>n>>x;
    tox(n);
    return 0;

}

中位数

定义：

中位数（Median）又称中值，对于有限的数集，可以通过把所有观察值

高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，
通常取最中间的两个数值的平均数作为中位数。

中位数可以代表样本与分布的性质，以及补充平均数的不足

例题：[洛谷-中位数](https://www.luogu.com.cn/problem/P1168)

题目描述：给定一个长度为 NN 的非负整数序列 AA，对于前奇数项求中位数。

我们可以使用STL来进行计算

vector q;  //定义一个int类型的一维数组，数组名称q；
常用函数:
 - q.size() //返回vector的实际长度
 - q.empty()  //判断是否为空，是则返回true，没有空返回false
 - q.front()  //返回vector的第一个元素
 - q.back()  //返回vector的最后一个元素
 - q.push_back(x); //将元素x插入到vector的最后面
 - q.pop_back()  //删除vector的最后一个元素，没有返回值
 - q.insert(pos，x)    //在vector中pos位置插入一个元素x
 - lower_bound(q.begin(),q.end(),x) //查找第一个大于或者等于x的位置
 - upper_bound(q.begin(),q.end(),x) //查找第一个大于x的位置

代码演示

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
vector<int> p;
int n;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		int x;
		scanf("%d",&x);//速度比cin要快
		p.insert(upper_bound(p.begin(),p.end(),x),x);//保证数组单调性
		if(i&1){    //  &1相当于%2，如果是奇数就输出
			printf("%d\n",p[(i-1)/2]);  //vector是从第0项开始存储的
		}
	}
	return 0;
}

质数

定义：

又称“素数”，该数只有1和该数本身两个正因数

质数常见性质与内容：

1.质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数的数称为质数。

2.互质指的是除了1，没有其他的公因子。

3.素数p的欧拉函数为p-1，且两个素数之间的非素数的欧拉函数的值小于第一个素数的欧拉函数的值。

4.唯一分解定理：任一大于1的自然数，要么本身是质数，要么可以分解为几个质数之积，且这种分解是唯一的。

5.若n为正整数，在 n*n到 （n+1）*（n+1） 之间至少有一个质数。

6.若n为大于或等于2的正整数，在n到 n！之间至少有一个质数。

7.若质数p为不超过n( n>=4)的最大质数，则 p>(n/2) 。

8.所有大于10的质数中，个位数只有1,3,7,9。

9.对于任意的整型N，分解质因数得到N= P1^x1 * P2^x2* …… * Pn^xn，则N的因子个数M为 M=（x1+1） * （x2+1） * …… *（xn+1）。

10.n的欧拉函数为ans,那么1~n/2内与n互质的数为ans/2,因为gcd(n,m)=gcd(n,(n-m))。

11.素数定理：不超过 x 的素数的个数近似为x / In(x)

首先，我们要知道如何判断一个数是不是质数

#include
using namespace std;
int is_zhishu(int n){
	if(n==1) return 0;
	for(int i=2;i<=n/i;i++){
	//当一个数n不是质数时，必定存在两个约数，一个大于或等于sqrt(n),另一个小于sqrt(n)
	    if(n&1==0&&n!=2) return 0; //除了2以外，所以质数都是奇数；
		if(n%i==0) return 0;
	}
	return 1;
}
int main(){
	int a;
	cin>>a;
	int p=is_zhishu(a);
	if(p) cout<<"YES";
	else cout<<"NO";
	return 0;
}

此外还有优化版的：

#include
using namespace std;
queue<int>q;//定义一个队列，先进先出
int k,x;
int main(){
	scanf("%d,%d",&k,&x);
	int f=0;
	q.push(k);
	while(q.size()){//也就是!q.empty();
		int t=q.front();
		q.pop();
		if(t==x){
		   f=1;
		   break;
		}else if(t<x){
			int x1=t*2+1;
			int x2=t*3+1;
			q.push(x1);
			q.push(x2);
		}
	}
	if(f) cout<<"YES";
	else cout<<"NO";
	return 0;
}

在平常练题中，经常需要我们构建一个素数表（打标）

我们可以根据质数的一些性质得到一些质数

//欧拉筛
#include 
using namespace std;
int cnt;
bool vis[10000001];
int p[10000001];
int b[100000];
void is_sh(int n){
   for(int i=2;i<=n;i++){
   	if(!vis[i]) p[++cnt]=i;
   	for(int j=1;j<=cnt&&p[j]*i<=n;j++){
   		vis[p[j]*i]=true;
   		if(!i%p[j]) break;
	   }
   }
}

int main(){
    is_sh(100001);//在10的5次方范围内筛素数
    for(int i=1;i<=100;i++) cout<<p[i]<<" ";
    return 0;
}

开根

谈起开根号，我们可以直接使用一个函数：

double x;
cin>>x;
cout<

此外，牛顿为我们提供了一种方法，我们称之为**“牛顿迭代方程”**

推荐链接如下

[牛顿迭代法](https://blog.csdn.net/melonyzzZ/article/details/127655972?spm=1001.2014.3001.5506)

简言之：

这是一种用迭代求方程近似根的方法，思路就是不断取切线，用线性方程的根逼近非线性方程 f(x) = 0 的根。

比如我们要求a的平方根，就是 求二次方程 f(x) = x^2 - a = 0（a >= 0）的根，其中f(x)的导数 f'(x) = 2x，利用牛顿迭代公式，则有：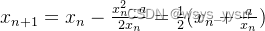

代码如下：

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
double square_root(double a){
	if (a < 0){
		return -1;
	}
	double t = a;  // t 为近似值
	while (fabs(t * t - a) > 1e-10){//fabs()函数为绝对值函数。
		t = (t + a / t) / 2.0;
	}
	return t;
}
int main(){
	double a = 0.0;
	scanf("%lf", &a);
	double ret = square_root(a);
	printf("%lf\n", ret);
	return 0;
}

数列

前缀和

求和一般有：数组前n项求和，区间求和。

一般情况下我们用一个数组加一个for循环，利用前缀和的知识即可

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
int a[N];
int sum[N];
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		sum[i]=sum[i-1]+a[i];
		//前缀和
	}
	for(int i=1;i<=n;i++){
		cout<<sum[i]<<" ";
	}
	cout<<endl;
	int m;
	cin>>m; //查询区间和次数
	while(m--){
		int x,y;
		scanf("%d%d",&x,&y);
		cout<<sum[y]-sum[x-1]<<" ";
	}
	return 0;
}

或者这样

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
int h[N];
int main(){
	int n=0;
    while(cin>>h[n++]);
	n--;
	……
	return 0;
}

然而当数据量非常大时，我们就需要采用另一种方式：线段树。

在这里我们需要了解：线段树是一种二叉树，并不是完全二叉树。对于每个父亲节点的编号 i，他的两个儿子的编号分别是 2*i 和 2*i+1。同时因为二进制位左移一位代表着数值 ×2，而如果左移完之后再或上 1，由于左移完之后最后一位二进制位上一定会是 0 ，所以 ∣1 等价于 +1 。

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
int a[N];
struct Tree{ 
	int left,right;
	int data;
}t[4*N];
void build_tree(int p,int l,int r){
	t[p].left =l;
	t[p].right =r;
	if(l==r){
		t[p].data =a[l];
	}
	else{
		int mid=l+r>>1;
		build_tree(p<<1,l,mid);
		build_tree(p<<1|1,mid+1,r);
		t[p].sum =t[p<<1].sum +t[p<<1|1].sum;
		//由于我们是要通过子节点来维护父亲节点，所以t[p].sum的位置应当是在回溯时。
	}
}
int ask(int p,int l,int r){
	if(l<=t[p].left &&t[p].right <=r) return t[p].sum ;
	int mid=(t[p].left +t[p].right)>>1;
	int ans=0;
	if(l<=mid) ans+=ask(p<<1,l,r);
	if(r>mid) ans+=ask(p<<1|1,l,r);
	return ans;
}
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build_tree(1,1,n);
	int m;
	cin>>m;
	while(m--){
		int L,R;
		scanf("%d%d",&L,&R);
		cout<<ask(1,L,R)<<"\n";
	}
	return 0;
}

最值（最大值）

## 最长上升子序列
#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
int a[N];
struct Tree{
	int left,right;
	int lmax,rmax;
	int data;
}t[4*N];
void build_tree(int p,int l,int r){
	t[p].left =l;
	t[p].right =r;
	if(l==r){
	  t[p].data=a[l];
		t[p].lmax =a[l];
		t[p].rmax =a[l];
	}
	else{
		int mid=l+r>>1;
		build_tree(p<<1,l,mid);
		build_tree(p<<1|1,mid+1,r);
		t[p].sum =t[p<<1].sum +t[p<<1|1].sum;
		t[p].lmax =max(t[p<<1].lmax ,t[p<<1].sum +t[p<<1|1].lmax );
		t[p].rmax =max(t[p<<1|1].sum +t[p<<1].rmax ,t[p<<1|1].rmax );
		t[p].data =max(t[p<<1].data ,max(t[p<<1|1].data ,t[p<<1].rmax +t[p<<1|1].lmax ));
	}
}
int ask(int p,int l,int r){
	if(l<=t[p].left &&t[p].right <=r) return t[p].data ;
	int mid=(t[p].left +t[p].right)>>1;
	int ans=-(1<<30);
	if(l<=mid) ans=max(ans,ask(p<<1,l,r));
	if(r>mid) ans=max(ans,ask(p<<1|1,l,r));
	return ans;
}
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build_tree(1,1,n);
	int m;
	cin>>m;
	while(m--){
		int L,R;
		scanf("%d%d",&L,&R);
		cout<<ask(1,L,R)<<"\n";
	}
	return 0;
}

斐波那契数列

Fibonacci 数列满足，

//矩阵快速幂+斐波那契数列 
#include
using namespace std;
#define il inline;
#define  re register
typedef long long ll;
const int N=1e9+7;
struct node{
	ll mat[3][3]; 
};
node z;
node matcf(node x,node y){
	memset(z.mat,0,sizeof(z.mat));
	for(int i=1;i<=2;i++){
		for(int j=1;j<=2;j++){
			for(re int k=1;k<=2;k++){
				z.mat[i][j]=(z.mat [i][j]+(x.mat[i][k])%N*(y.mat [k][j])%N)%N;
			}
		}
	}
	return z;
}
node matpow(int k){
	node t,a;
	t.mat[1][1]=1;			
	t.mat[1][2]=0;
	t.mat[2][1]=0;
	t.mat[2][2]=1;
	a.mat[1][1]=1;			
	a.mat[1][2]=1;
	a.mat[2][1]=1;
	a.mat[2][2]=0;
	while(k){
		if(k&1){
			t=matcf(t,a);
		}
		k>>=1;
		a=matcf(a,a);
	}
	return t;
	
}
int n,m;
int main(){
	scanf("%d",&n);
	node temp;
	temp=matpow(n-1);
	ll ans=temp.mat [1][1];
	printf("%lld\n",ans%N);
	return 0;
}

偏序集概念+Dilworth定理

Dilworth 定理

对于任意有限偏序集，其最大反链中元素的数目必等于最小链划分中链的数目。此定理的对偶形式亦真。

补充一下对链和反链的定义：
设 C 是偏序集的一个子集，如果 C 中元素互相可比，那么称 C 是链；如果 C 中元素互相不可比，则称 C 是反链。
可以视为链对应到哈斯图上就是一条从下至上的 “链”（有向路径）。

未完待续