数据结构 哈希表 整数哈希表
哈希表是可以根据关键字的值,直接查询和访问的数据结构
简单整数哈希的概念
查找时
适用条件,数组内的数不能太大,适合元素数小,但数组长时的查找
例如一共有一万个数,每个最大不超过100,放在一个数组a[N]内
查找i是否在a[N]内出现,每次查找,要遍历循环100次
但是此时我们可以新建一个标记数组,f[N],f[i]=0,则代表i没有在a[N]中出现
f[i]=1,表示出现一次,f[i]=2,表示出现两次......,我们在读入时,在f[N]数组内也做上标记即可
排序时
适用条件,数组内的数不能太大,适合元素数小,但数组长时的排序
排序也同样依赖f[N]数组,和查找时的f[N]一个意义
例如一共有一万个数,每个元素范围0-99,放在一个数组a[N]内
新建一个标记数组,f[N],f[i]=x,则代表i在a[N]中出现x次,
首先,他的下标其实是a[N]中的元素的值,下标本来就是顺序排列,不用再排列顺序
然后,我们要把排序后的元素,放到数组s[N]中
那排序时,只需要顺序遍历f[N]数组即可
例如,f[0]=0,f[1]=2
代表0在a[N]中出现0次,不需要将0放入s[n]
f[1]=2代表1在f[n]中出现两次,在s[n]数组内放入两个1,即可
以此类推,f[n]数组循环完,s[n]即排序完成的数组
超大,多类型哈希
前面一直在说适用于数组中数据范围小,且是整数的情况下,使用简单哈希
如果遇到更多更大数据范围呢
此时我们可以使用哈希函数
哈希函数
思想,创造一个函数,将待存储的数据,转换为数组长度范围内整数,
例如简单说,就是把范围是10的九次方,个数是10的五次方的数据,存储到10的五次方的映射数组里
例如数组长度是100
例如待存储数据是字符串
我们可以将每个字符的asc码相加得到一个整数,将整数模除100,把对应的值存储到数组
但是这样会导致,数组里存储的值,并不精确对应,例如ab,ba两个字符串,都对应一个整数
为了解决这个问题,有两种方法:拉链法,开放寻址法
数组的长度选择
因为数据要整除数组长度,所以数组长度选择也是有技巧的,选择质数,往往可以让重复元素最少
拉链法
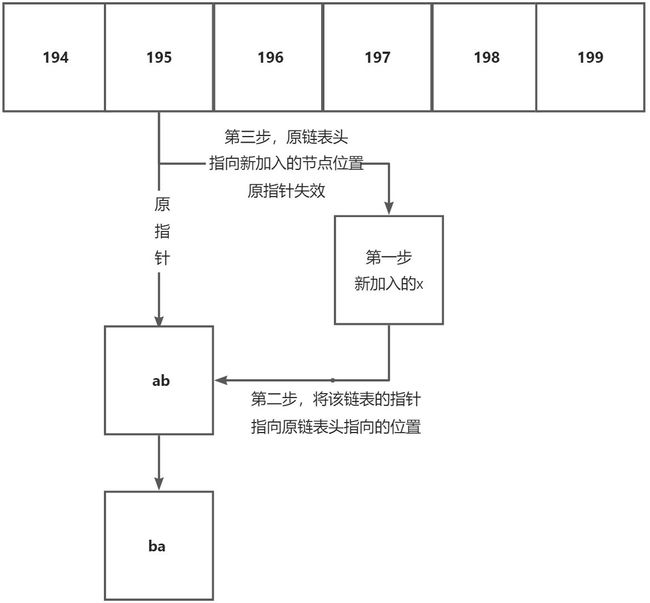
先是一个普通数组h[N],当数组内有元素添加时,我们在该数组位置上,向下拉一个链子
例如ab,ba字符串,都对应一个整数值195,那在数组h[195]下,向下拉两个节点,分别存储ab,ba
下拉节点相当于一个链表,所以我们还需要两个数组,e[N]用来存储值,ne[N]用来存储下一个值在什么地方
插入
void insert(int x){
//k是上图中,194,195,也就是经过哈希函数后,在数组中存储的下标位置
//%N+N%N能保证K不为负数,因为数组下标不能为负,c++直接负数模正整数其实还是负数,例如-10%3=-1
int k= (x%N+N)%N;
//经典链表头插入,h[k]其实就是列表头
//第一步,在存储值的链表数组e[]内添加上x
e[idx]=x;
//第二步,将该链表的指针,指向原链表头指向的位置
ne[idx]=h[k];
//第三步,原链表头,指向新加入的节点位置
h[k]=idx;
//此idx节点值已经用过,idx++,方便下次循环直接用
idx++;
}查询
int find(int x){
//同样找到映射位置
int k=(x%N+N)%N;
//遍历h[k]下的链表,查看是否有x,有则返回1,直接结束函数
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x)return 1;
}
//没查到,返回0
return 0;
}拉链法例题和完整代码
AcWing - 算法基础课
#include
using namespace std;
const int N = 100003;
int h[N],e[N],ne[N],idx;
void insert(int x){
int k= (x%N+N)%N;
e[idx]=x;
ne[idx]=h[k];
h[k]=idx;
idx++;
}
int find(int x){
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i]){
if(e[i]==x)return 1;
}
return 0;
}
int main(){
for(int i=0;i>n;
while(n--){
char c;int x;
cin>>c>>x;
if(c=='I'){
insert(x);
}
else{
cout<<(find(x)?"Yes":"No")< 开放寻址法
memset--清零数组函数
开放寻址法,需要先把数组初元素,始化为一个不在题目范围内的超大数
代表意义为空,可以使用memset函数,大量节省时间
题目
AcWing - 算法基础课
开放寻址的概念
在把x(原元素)映射为k后,检查h[k]上是否有元素,如果有,k++,直到k位置上为为空
映射关系是int k= (x%N+N)%N; N=200003(建议数组长度为题目数量N的两倍到三倍,不容易映射重复)
示例:当要数组中已经存储了11,还要存储2000014时(他们俩的映射出的k相同),如下图
这样做,可以把大数存入小数组内
在查找数组中是否有元素x时,只需要查询和x映射k相连的非空数组内,那几个数,是否有x即可
完整代码
#include
#include
using namespace std;
const int N = 300003;
const int nulls = 0x3f3f3f3f;//定义一个不在范围内的数,代表意义为空
int h[N],e[N],ne[N],idx;
//find函数,返回一个已经有x,或者可以放入x的位置k
int find(int x){
int k=(x%N+N)%N;
//已经有x,或者可以放入x则结束循环
while(h[k]!=nulls&&h[k]!=x){
k++;
//k=n数组长度用完了,要从头开始重置
if(k==N)k=0;
}
return k;
}
int main(){
memset(h,0x3f,sizeof h);
int n;
cin>>n;
while(n--){
char c;int x;
cin>>c>>x;
int k=find(x);//查询到已经有x,或者可以放入x的空位置k
if(c=='I'){
h[k]=x;//插入,将该位置放入x
}
else{
//查询,判断该位置是否为空,不为空则是有x的位置
cout<<(h[k]!=nulls?"Yes":"No")<