【机器学习】详解 Optimizers
目录
一、简介
二、原理
2.1 BGD (Batch Gradient Descent)
2.2 SGD (Stochastic Gradient Descent)
2.3 MBGD (Mini-Batch Gradient Descent)
2.4 BGD、SGD、MBGD 小结
2.5 SGDM (Stochastic Gradient Descent with Momentum)
2.6 AdaGrad (Adaptive Gradient)
2.7 RMSProp (Root Mean Square Propagation)
2.8 Adam (Adaptive Moment Estimation)
2.9 AdamW (Adaptive Moment Estimation with Weight-decay)
三、延伸
3.1 经典优化器效果图示
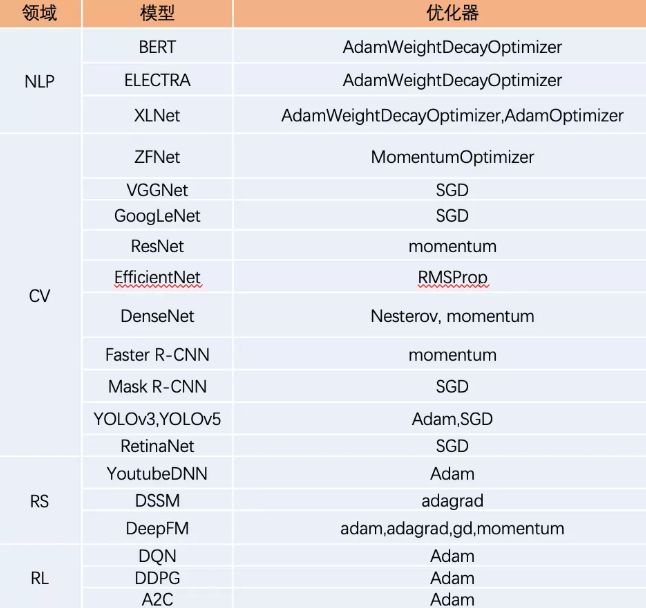
3.2 经典深度学习模型的优化器
3.3 经典优化器的相关论文
3.4 优化器的相关经验
3.5 SGD 有多种改进,但为什么还是用 SGD 较多?
一、简介
假如定义了一个机器学习模型,就希望该模型能够尽可能拟合所有训练数据。如何评价模型对数据的拟合程度呢?使用的评估指标称为 损失函数 (Loss Function),当损失函数值下降,就可以认为模型对数据的拟合程度又一步提升了。损失函数的平均值最小之时,即可认为模型对指定训练数据的拟合程度最佳之际。为降低损失函数数值,需使用各种优化算法进行优化。优化器 / 优化算法 在深度学习反向传播过程中,指引损失函数的各个参数往正确的方向更新合适的值,使得更新后的各个参数让损失函数的值不断逼近 全局极小值。
更具体地,在机器学习中,优化问题的 目标函数 / 损失函数 / 代价函数 通常可表示为:
![]()
其中, 表示待优化的模型参数, 表示模型的输入数据/样本, 表示模型的输出结果/预测, 表示输入数据/样本的标签/目标 (Ground Truth),函数 刻画了模型在样本对 上的损失, 表示数据分布, 表示期望。因此, 刻画了当参数为 时,模型在所有数据上的平均损失。训练模型即希望能够找到平均损失最小的模型参数,也就是求解优化问题:
![]()
当然,在深度学习这种通常非凸优化背景下,找到的通常是 局部极小值。
二、原理
2.1 BGD (Batch Gradient Descent)
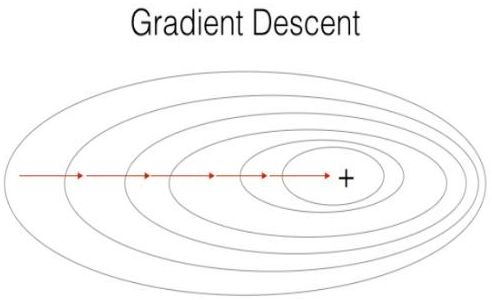
GD (梯度下降),又称 BGD (批量梯度下降) 作为经典梯度下降法,其 在更新每一个模型参数时,都令所有样本 (样本全集) 参与更新计算,即在整个训练集上计算损失函数关于模型参数的梯度。其思想可以比喻为在下山之前掌握了附近的地势情况,选择总体平均梯度最小的方向下山。
BGD 采用所有训练数据的平均损失来近似目标函数,即:
![]()
![]()
其中, 表示训练样本数, 为梯度算子, 为目标函数 的梯度。此时,模型参数 的更新公式为:
BGD 的优点:
迭代次数相对较少,在凸函数上能保证收敛到全局最优点。
BGD 的缺点:
每一次对模型参数 进行更新时,需在整个训练集上计算梯度。当样本总数 很大时,过高的计算量将耗费很长的计算时间与大量的计算资源 (训练集太大不能全部载入内存),且无法投入新数据实时更新模型 (在线学习),因此在实际应用中 BGD 基本不可行。
2.2 SGD (Stochastic Gradient Descent)
SGD (随机梯度下降) 用 单个训练样本的损失来近似平均损失,即
![]()
![]()
此时,模型参数 的更新公式为:
SGD 的优点:
SGD 用单个样本即可对模型参数进行一次更新,解决了 BGD 进行的大量冗余计算,大大加快了收敛速率。SGD 也非常适用于数据不断加入的在线更新场景 (在线学习)。
SGD 的缺点:
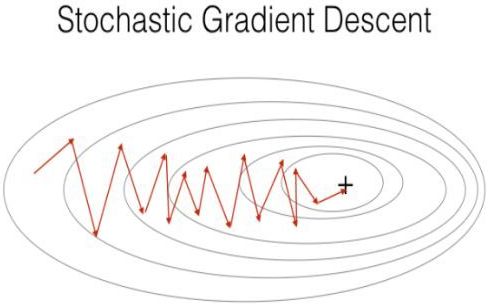
SGD 以高方差的特点进行频繁的连续参数更新,使得损失函数值严重震荡,无法保证每次都向着整体最优化方向迭代,甚至可能在全局最优值处来回震荡乃至跳出全局最优值。
SGD 的 PyTorch 例子:
# https://pytorch.org/docs/stable/generated/torch.optim.SGD.html#torch.optim.SGD
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()2.3 MBGD (Mini-Batch Gradient Descent)
不同于每次使用所有样本的 GD 和 每次仅用单个样本的 SGD,MBGD (小批量梯度下降) 介于二者之间,每次使用训练数据的一个子集 (mini-batch) 进行模型参数的更新。
假设每次模型参数更新时,同时处理 个 () 训练数据 ,则目标函数及其梯度为:
![]()
![]()
此时,模型参数 的更新公式为:
MBGD 的优点:
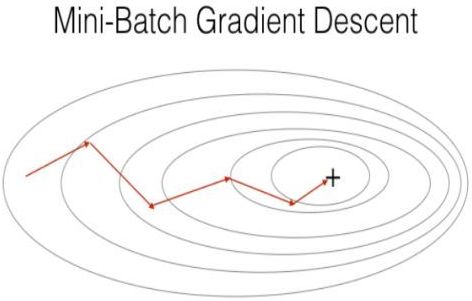
降低了 SGD 的高方差,从而使得迭代算法更加稳定 (如同 BGD 的优点),也为了充分利用高度优化的矩阵运算操作,使运算速度远优于 BGD (如同 SGD 的优点)。虽然 MBGD 在更新过程中看起来波动也不小、也会走弯路,但大量的理论和实践工作证明,只要噪声不是特别大,都能很好收敛。
MBGD 的缺点:
1. MBGD 无法保证较好的收敛性。MBGD 每次仅用数据集中的一部分进行梯度下降,所以每次下降并不严格按照朝损失函数的最小方向下降,而只是总体下降趋势朝着最小方向,因此极易陷入局部最小值。
2. MBGD 受到学习率设置的影响较大。若学习率太小,则收敛速度会很慢 (如同 BGD 的缺点);若学习率太大,则损失函数就会在极小值处不停震荡甚至偏离 (如同 SGD 的缺点)。
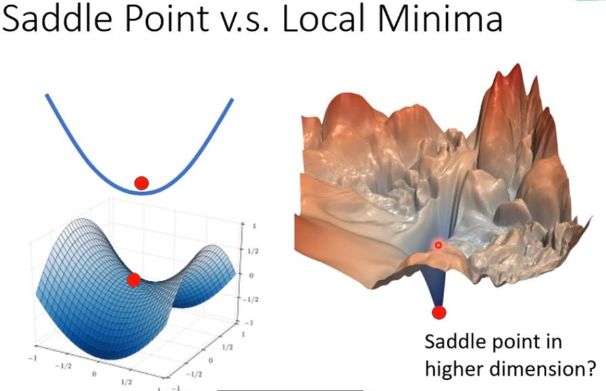
3. 对于非凸函数,MBGD 还要避免陷于梯度为 0 的驻点 (Stationary Point) —— 局部极大/小值点和鞍点。特别是鞍点周围的梯度都接近于 0,很容易困于其中。鞍点 (Saddle Point) 得名于其形状类似于马鞍,鞍点通常被一个具有相同误差的平面所包围。一个光滑函数的鞍点,其邻域的曲线、曲面或超曲面都位于鞍点的切线的不同边。对于神经网络而言,一个关键挑战便是避免陷入鞍点,即损失函数在该点的一个维度上是上坡,而在另一个维度上是下坡。尽管它在一个方向上是一个最小值点,但是它在另一个方向上却是局部最大值点,这使得梯度下降法非常难于逃脱,因为在各个维度上梯度都趋近于 0。若它沿着 x 方向变得更平坦的话,梯度下降便会在 x 轴振荡并且不能继续根据 y 轴下降,这就会给我们一种已经收敛到最小值点的错觉。
MBGD 使用注意事项:
1. 如何选取参数 mini-batch size ? 在不同应用中,最优的 通常不同,需通过调参确定。mini-batch size 越大,每个 epoch 的迭代次数越少,训练时间就更快;而 mini-batch size 越小,每个 epoch 的迭代次数更多,训练更耗时。一般 取 2 的幂次时能充分利用矩阵运算操作,所以可优先在 2 的幂次中挑选,例如 16、32、64、128、256 等等。
2. 如何挑选 个训练数据? 为避免样本的特定顺序给算法收敛带来影响,通常在每次遍历训练样本前,先对所有样本进行打乱/混洗 (shuffle),然后在每次迭代 (iter) 时按顺序挑选 个样本,直至遍历完所有的数据 (一个 epoch)。
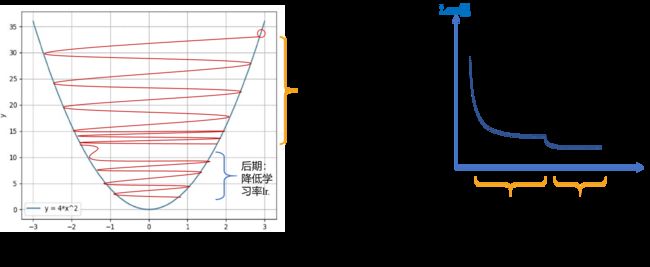
3. 如何选取步长/学习率 ? 为加快收敛速率,同时提高求解精度,通常会采用 学习率衰减方案 (learning rate decay scheduler):一开始算法采用较大的学习率, 当误差曲线进入平台期后,再减小学习率进行更精细的调整和学习。当然,最优的学习率衰减方案也通常需要调参才能得到。
2.4 BGD、SGD、MBGD 小结
做个比喻。假设有一人正在下山,其视力很好乃至能看清自己所处位置的坡度,那么沿坡向下最终可达山底。若被蒙上双眼,只能凭脚底踩石头的感觉判断当前位置的坡度,精确性就会大大下降。有时他认为的坡,实际上可能并不是坡,走上一段时间发现还没有下山,或曲曲折折绕了好多弯路才下山。类似地,BGD 就好比正常下山,而 SGD 就好比蒙着眼睛下山。
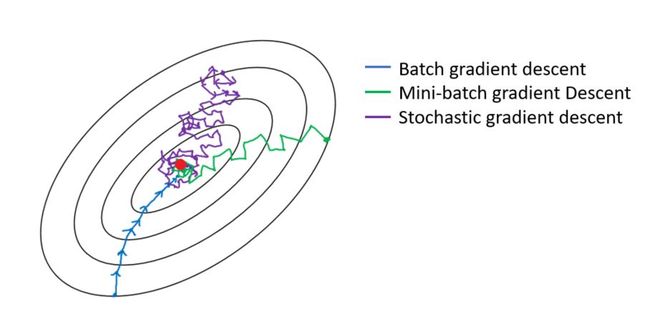
更具体地,BGD 在全部训练集上计算准确的梯度,SGD 则采样单个样本来估计的当前梯度。为获取准确的梯度,BGD 的每一步都把整个训练集载入进来进行计算,时间花费和内存开销都非常大,无法应用于大数据 / 大模型的场景。相反,SGD 则放弃了对梯度准确性的追求,每步仅仅随机采样一个样本来估计当前梯度,计算速度快,内存开销小。但由于每步接受的信息量有限,SGD 对梯度的估计常常出现偏差,造成目标函数曲线收敛得很不稳定,伴有剧烈波动,有时甚至出现不收敛的情况。而 MBGD 则作为 BGD 和 SGD 的折中方法,兼具二者的优点 (和缺点)。下图展示了三种方法在优化过程中的参数轨迹,可见 BGD 稳定地逼近最低点, 而 SGD 的参数轨迹曲曲折折堪比 “黄河十八弯”,MBGD 的轨迹抖动程度则居中。
进一步地,深度学习中的优化问题本身就很难,有太多局部最优点的陷阱,它们对而言梯度下降法都是普遍存在的。但对 SGD 来说,最可怕的不是局部最优点,而是 山谷和鞍点。山谷即狭长的山间小道,左右两边是峭壁;鞍点形如马鞍,一个方向上两头翘,另一方向上两头垂,而中心区域是一片近乎水平的平地。为什么 SGD 最害怕遇上这两类地形呢?在山谷中,准确的梯度方向是沿山道向下,稍有偏离就会撞向山壁,而 SGD 粗糙的梯度估计使得它在两山壁间来回反弹震荡,不能正确地沿山道方向迅速下降,导致收敛不稳定和收敛速度慢。在鞍点处, SGD 会走入一片平坦之地 (此时离最低点还很远,故也称 Plateau)。想象一下蒙着双眼只凭借脚底感觉坡度,如果坡度很明显,那么基本能估计出下山的大致方向;如果坡度不明显,则很可能走错方向。同样,在梯度近乎为零的区域,随机梯度下降法无法准确察觉出梯度的微小变化,结果就停滞下来,举步维艰。
2.5 SGDM (Stochastic Gradient Descent with Momentum)
SGDM (带动量的随机梯度下降) 在 SGD 的基础上加入了一阶动量,其模拟物理里动量的概念,积累之前的动量来替代真正的梯度。直观地,SGDM 相当于加入了一个 惯性,使得在坡度较陡的地方惯性较大,从而下降就比较快;坡度平缓的地方惯性较小,从而下降得比较慢。SGDM 的梯度更新公式为:
![]()
![]()
SGDM 通过加入动量 及其衰减系数 (常取 0.9),在梯度下降过程中可 在梯度方向不变的方向上加快下降速度、在梯度方向有所改变的方向上减慢下降速度。举个例子:为解决 SGD 在山谷震荡和鞍点停滞 的问题,想象一个 纸团 在山谷和鞍点处的运动轨迹,在山谷中纸团受重力作用沿山道滚下,两边是不规则的山壁,纸团不可避免地撞在山壁,由于质量小受山壁弹力的干扰大,从山壁一侧反弹回来撞向另一侧,结果来回震荡地滚下;若当纸团来到鞍点的一片平坦之地时,还是由于质量小,速度很快减为零。纸团的运动情况好比 SGD 在山谷和鞍点遇到的问题。直观地,若将纸团换成 铁球,当其沿山谷滚下时,不易受到中途旁力的干扰,轨迹会更稳更直;当铁球到达鞍点中心处时,将在惯性作用下继续前行,从而有机会冲出平坦的陷阱。铁球的运动情况好比 SGDM 在山谷和鞍点应对的方法,因此,SGDM 相比 SGD 具有更强的鲁棒性。
更具体地,前进步伐 由两部分构成:一是学习率 乘以当前估计的梯度,这部分与 SGD 完全一致;二是带衰减的前一次步伐。此处,惯性就体现在对前一次步伐信息的重利用上。类比中学物理知识,当前梯度 就好比 当前时刻受力产生的加速度,而 前一次步伐 好比 前一时刻的速度,当前步伐 好比 当前时刻的速度。为计算当前时刻的速度,应当考虑前一时刻速度和当前加速度共同作用的结果,因此 直接依赖于和,而不仅仅是。另外,衰减系数 扮演了 阻力 的作用。因为刻画惯性的物理量是 动量,所以该算法名为 SGDM (带动量的随机梯度下降)。沿山谷滚下的铁球,会受到沿坡道向下的力和与左右山壁碰撞的弹力。向下的力稳定不变,产生的动量不断累积,速度越来越快;左右的弹力总是在不停切换,左右侧动量累积的结果是相互抵消,从而减弱了球在左右侧的来回震荡。因此,与 SGD 相比,SGDM 收敛速度更快,收敛曲线也更稳定 (解决 SGD Hessian 矩阵病态问题),如下图所示:
SGDM 的 PyTorch 例子:
# https://pytorch.org/docs/stable/generated/torch.optim.SGD.html#torch.optim.SGD
>>> optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()SGDM 的朴素实现:
# http://t.zoukankan.com/xiximayou-p-12713594.html
class StochasticGradientDescent():
def __init__(self, learning_rate=0.01, momentum=0):
self.learning_rate = learning_rate
self.momentum = momentum
self.w_updt = None
def update(self, w, grad_wrt_w):
# If not initialized
if self.w_updt is None:
self.w_updt = np.zeros(np.shape(w))
# Use momentum if set
self.w_updt = self.momentum * self.w_updt + (1 - self.momentum) * grad_wrt_w
# Move against the gradient to minimize loss
return w - self.learning_rate * self.w_updt2.6 AdaGrad (Adaptive Gradient)
除了 基于历史信息获得的惯性,我们还期待 获得对周围环境的感知。即使蒙上双眼,依靠前几次迈步的感觉,也应该能判断出一些信息,比如这个方向总是坑坑洼洼的,那个方向可能很平坦。SGD 对环境的感知是指 在参数空间中,根据不同参数的一些经验性判断,自适应地确定参数的学习率,使得不同参数具有不同的更新步幅。例如,在文本处理中训练词嵌入模型的参数时,有的词或词组频繁出现,有的词或词组则极少出现。数据的稀疏性导致相应参数的梯度的稀疏性,不频繁出现的词或词组的参数的梯度在大多数情况下为零,从而这些参数被更新的频率很低。在应用中,我们希望更新频率低的参数可以拥有较大的更新步幅,而更新频率高的参数的步幅可以减小。AdaGrad 采用 二阶动量 —— “历史梯度平方和”,即 所有时刻的梯度值的平方和 来 衡量不同参数的梯度的稀疏性 (历史更新频率),取值越小则表明越稀疏 (参数更新频率越低)。AdaGrad 的参数更新公式为:
其中, 表示 时刻的参数向量 的第 个参数, 表示 时刻的梯度向量 的第 个维度 (方向),平滑参数项 用于防止学习率 的分母为 0。
此外,分母中历史梯度平方和的求和的形式实现了 退火过程,这是很多优化技术中常见的策略。这意味着 随着时间推移,分母将随之增大,从而学习率 将越来越小,从而保证了算法的最终收敛。但若分母增加得过大,学习率 将过于接近 0,从而无法有效更新参数,造成反面效果。例如可能使得训练过程提前结束,即便后续还有数据也无法学到有用的知识。事实上,虽然在 RMSProp 的优化下,不同参数有了各自的学习率,但初始的全局学习率仍需手工指定。若全局学习率过大,优化同样不稳定;而若全局学习率过小,则可能还没有到极值就停滞不前了。
可见,AdaGrad 本质上是对学习率施加了一个 约束:对于经常更新的参数,已积累了大量关于它的知识,不希望被单个样本影响太大,即学习率可低一些;对于偶尔更新的参数,了解的信息严重不足,希望能从每个偶尔出现的样本中多学一些,即学习率可高一些。此前的 SGD 及其变体的优化器主要聚焦在优化梯度前进的方向上,而 AdaGrad 首次使用二阶动量来关注学习率,开启了自适应学习率算法的里程。虽然AdaGrad 算法 不能保证找到极值点,但是它很 适合处理稀疏梯度,在 稀疏数据场景 下表现非常好。
AdaGrad 的 PyTorch 例子:
# https://pytorch.org/docs/stable/generated/torch.optim.Adagrad.html#torch.optim.Adagrad
>>> optimizer = torch.optim.Adagrad(model.parameters(), lr=0.01)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()AdaGrad 的朴素实现:
# http://t.zoukankan.com/xiximayou-p-12713594.html
class Adagrad():
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
self.G = None # Sum of squares of the gradients
self.eps = 1e-8
def update(self, w, grad_wrt_w):
# If not initialized
if self.G is None:
self.G = np.zeros(np.shape(w))
# Add the square of the gradient of the loss function at w
self.G += np.power(grad_wrt_w, 2)
# Adaptive gradient with higher learning rate for sparse data
return w - self.learning_rate * grad_wrt_w / np.sqrt(self.G + self.eps)2.7 RMSProp (Root Mean Square Propagation)
为解决 AdaGrad 学习率急剧下降 问题,RMSProp 对 AdaGrad 的二阶动量进行了改进,将历史梯度平方和改为其指数加权的移动平均,使得 RMSProp 在非凸背景下效果更好。RMSProp 的参数更新公式为:
![]()
![]()
![]()
其中,表示第 时刻的二阶动量 ,即梯度平方的指数加权的移动平均, 表示 时刻的梯度向量 的第 个维度 (方向),平滑参数项 用于防止学习率的分母为 0。
事实上,RMSProp 依然 依赖于全局学习率 ![]() 。RMSProp 算是 AdaGrad 的一种发展以及 AdaDelta 的变体,效果趋于二者之间。RMSProp 适合处理非平稳目标 (包括季节性和周期性) —— 对于 RNN 效果很好。
。RMSProp 算是 AdaGrad 的一种发展以及 AdaDelta 的变体,效果趋于二者之间。RMSProp 适合处理非平稳目标 (包括季节性和周期性) —— 对于 RNN 效果很好。
RMSProp 的 PyTorch 例子:
# https://pytorch.org/docs/stable/generated/torch.optim.RMSprop.html#torch.optim.RMSprop
>>> optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01, alpha=0.99)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()RMSProp 的朴素实现:
# http://t.zoukankan.com/xiximayou-p-12713594.html
class RMSprop():
def __init__(self, learning_rate=0.01, rho=0.9):
self.learning_rate = learning_rate
self.Eg = None # Running average of the square gradients at w
self.eps = 1e-8
self.rho = rho
def update(self, w, grad_wrt_w):
# If not initialized
if self.Eg is None:
self.Eg = np.zeros(np.shape(grad_wrt_w))
self.Eg = self.rho * self.Eg + (1 - self.rho) * np.power(grad_wrt_w, 2)
# Divide the learning rate for a weight by a running average of the magnitudes of recent
# gradients for that weight
return w - self.learning_rate * grad_wrt_w / np.sqrt(self.Eg + self.eps)2.8 Adam (Adaptive Moment Estimation)
Adam 集惯性保持和环境感知两个优点于一身,本质上是带有动量项的 RMSprop。一方面,Adam 记录梯度的一阶矩 (first moment),即过往梯度与当前梯度的平均,体现了惯性保持;另一方面,Adam 记录梯度的二阶矩 (second moment),即过往梯度平方与当前梯度平方的平均,体现了环境感知,为不同参数产生自适应的学习速率。一阶矩和二阶矩采用类似于滑动窗口内求平均的思想进行融合,即当前梯度和近一段时间内梯度的平均值,时间久远的梯度对当前平均值的贡献呈指数衰减。具体来说,一阶矩和二阶矩采用指数衰减平均 (exponential decay average) 技术,计算公式为
![]()
![]()
其中, 为一阶矩估计的指数衰减率 (常取 0.9) ,用于控制一阶矩估计; 为二阶矩估计的指数衰减率 (常取 0.999),用于控制二阶矩估计; 为 一阶矩 (mean), 为 二阶矩 (variance)。一阶矩相当于估计,由于当前时刻梯度 是随机采样得到的估计结果,因此更关注它在统计意义上的期望;二阶矩相当于估计,这不同于 AdaGrad 对 的历史累积和,而是 的期望。它们的 物理意义 在于:
- 当 大且 大时,梯度大且稳定,表明遇到一个明显的大坡,前进方向明确;
- 当 趋于零且 大时,梯度不稳定,表明可能遇到一个峡谷,易引起反弹震荡;
- 当 大且 趋于零时,这种情况不可能出现;
- 当 趋于零且 趋于零时,梯度趋于零,可能到达局部最低点,也可能走到一片坡度极缓的平地,此时要避免陷入平原 (plateau)。
另外,因为 mean 和 variance 的初始值为 0,所以它们会向 0 偏置。为减少这种偏置影响,Adam 还考虑了 和 在初始值为 0 时的 偏置矫正 和 。更具体地,Adam 的更新公式为:
![]()
![]()
![]()
Adam 的优点:
- 通过一阶、二阶动量,有效控制学习率和方向,防止梯度振荡和鞍点停滞
- 经偏置校正,每次迭代学习率都有一个固定范围 (初始学习率),使参数变化较为平稳
- 为不同的参数计算不同的自适应学习率,能自然地实现步长退火
- 参数的更新不受梯度的伸缩变换影响
- 超参数具有较好的解释性,且通常无需或仅需很少的微调
- 适用于大多数非凸优化问题、大数据集和高维空间
- 结合了 Adagrad 善于处理稀疏梯度和 RMSprop 善于处理非平稳目标的优点
- 实现简单,计算高效,对内存需求少
总之,Adam 成为了大部分情况下的默认优化器。
Adam 的缺点:
- 可能不收敛。二阶动量是固定时间窗口内的累积,随着时间窗口的变化,遇到的数据可能发生巨变,使得 可能时大时小,而不单调变化。这就可能在训练后期引起学习率的震荡,导致模型无法收敛。
- 可能错过全局最优解。自适应学习率算法可能会对前期出现的特征过拟合,后期才出现的特征很难纠正前期的拟合效果。Adam 后期 的学习率太低,影响了有效的收敛。
Adam 的 PyTorch 举例:
# https://pytorch.org/docs/stable/generated/torch.optim.Adam.html#torch.optim.Adam
>>> optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999))
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()Adam 的朴素实现:
# http://t.zoukankan.com/xiximayou-p-12713594.html
class Adam():
def __init__(self, learning_rate=0.001, b1=0.9, b2=0.999):
self.learning_rate = learning_rate
self.eps = 1e-8
self.m = None
self.v = None
# Decay rates
self.b1 = b1
self.b2 = b2
def update(self, w, grad_wrt_w):
# If not initialized
if self.m is None:
self.m = np.zeros(np.shape(grad_wrt_w))
self.v = np.zeros(np.shape(grad_wrt_w))
self.m = self.b1 * self.m + (1 - self.b1) * grad_wrt_w
self.v = self.b2 * self.v + (1 - self.b2) * np.power(grad_wrt_w, 2)
m_hat = self.m / (1 - self.b1)
v_hat = self.v / (1 - self.b2)
self.w_updt = self.learning_rate * m_hat / (np.sqrt(v_hat) + self.eps)
return w - self.w_updt2.9 AdamW (Adaptive Moment Estimation with Weight-decay)
L2 正则化 是减少过拟合的经典方法,它会向损失函数添加由模型所有权重的平方和组成的惩罚项,并乘上特定的超参数以控制惩罚力度。加入 L2 正则后,损失函数就变为:
![]()
一方面,带![]() 正则的 Adam 的更新公式为:
正则的 Adam 的更新公式为:
![]()
![]()
![]()
![]()
![]()
另一方面,带权重衰减的 Adam —— AdamW 的的更新公式为:
![]()
![]()
![]()
![]()
![]()
带 L2 正则的 Adam 与 AdamW 的对比:
可见,Adam 不考虑 L2 正则项的梯度,带 L2 正则的 Adam 在计算梯度时加入 L2 正则项的梯度,而 AdamW 在参数更新时加入 L2 正则项的梯度。使用带 L2 正则的 Adam 并不有效,因为若引入 L2 正则项,则在计算梯度时会加上 L2 正则项的梯度。而较大权重对应的梯度也较大,由于 Adam 参数更新时的减去项包含除以梯度平方的累积的步骤,从而较大权重的较大梯度将使得减去项偏小,使得权重越大 L2 正则项惩罚反而越小了 (即权重越大变化竟越大),达到相反的效果/目的。 而使用带权重衰减的 Adam 则对所有权重都采用相同的系数更新,权重越大显然惩罚越大 (即权重越大变化应越小)。
AdamW 广泛应用于 Transformer 模型中,且经常搭配学习率衰减策略 (scheduler) 使用。
AdamW 的 PyTorch 举例:
# https://pytorch.org/docs/stable/generated/torch.optim.AdamW.html#torch.optim.AdamW
>>> optimizer = torch.optim.AdamW(model.parameters(), lr=0.001, betas=(0.9, 0.999), weight_decay=0.01)
>>> optimizer.zero_grad()
>>> loss_fn(model(input), target).backward()
>>> optimizer.step()三、延伸
3.1 经典优化器效果图示
上图展现了 Adam 之前的经典优化算法在鞍点和等高线处的优化轨迹。可见,自适应优化算法 (Adagrad, Adadelta, Rmsprop) 几乎很快就找到了正确的方向并前进,收敛速度也相当快;而其它非自适应优化算法 (SGD, Momentum, NAG) 要么很慢,要么走了很多弯路才找到。
3.2 经典深度学习模型的优化器
| 优化器 |
论文 |
| SGD |
Robbins, H., & Monro, S. (1951). A stochastic approximation method. The annals of mathematical statistics, 400-407. |
| NAG |
Nesterov, Y. (1983). A method for unconstrained convex minimization problem with the rate of convergence O (1/k^ 2). In Doklady an ussr (Vol. 269, pp. 543-547). |
| momentum |
Qian, N. (1999). On the momentum term in gradient descent learning algorithms. Neural networks, 12(1), 145-151. |
| AdaGrad |
Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of machine learning research, 12(7). |
| AdaDelta |
Zeiler, M. D. (2012). Adadelta: an adaptive learning rate method. arXiv preprint arXiv:1212.5701. |
| Adam& AdaMax |
Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. |
| AdamW |
Loshchilov, I., & Hutter, F. (2017). Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101. |
| Nadam |
Dozat, T. (2016). Incorporating nesterov momentum into adam. |
| Lookahead |
Zhang, M. R., Lucas, J., Hinton, G., & Ba, J. (2019). Lookahead optimizer: k steps forward, 1 step back. arXiv preprint arXiv:1907.08610. |
| RAdam |
Liu, L., Jiang, H., He, P., Chen, W., Liu, X., Gao, J., & Han, J. (2019). On the variance of the adaptive learning rate and beyond. arXiv preprint arXiv:1908.03265. |
| AMSGRAD |
Reddi, S. J., Kale, S., & Kumar, S. (2019). On the convergence of adam and beyond. arXiv preprint arXiv:1904.09237. |
3.4 优化器的相关经验
- 各优化算法孰优孰劣并无定论,有时理论上好并不能代表实际也佳。刚入门推荐优先考虑 SGDM 和 Adam。
- Adam 等自适应学习率算法对稀疏数据颇具优势,且收敛很快,故对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,且最好采用默认值;SGD 系列通常训练时间更长,但是在好的初始化和学习率调度下 (精调) 的 SGDM 往往能取得最佳结果。
- 根据你的需求来选择 —— 若要快速验证新模型效果,且需要训练较深较复杂的网络时,可先用 Adam 快速优化;在模型上线或者结果发布前,可以用精调的 SGD 系列优化算法进行模型的极致优化。
- 考虑不同算法的组合。例如先用 Adam 快速接近收敛,然后切换到 SGDM 系列充分调优。
- 添加梯度噪声 (高斯分布 ) 到参数更新中,可使网络对不良初始化更加 robust,并有助于训练特别深而复杂的网络。
3.5 SGD 有多种改进,但为什么还是用 SGD 较多?
因为 SGD (with Momentum) 依然常为实践效果更好的方法。
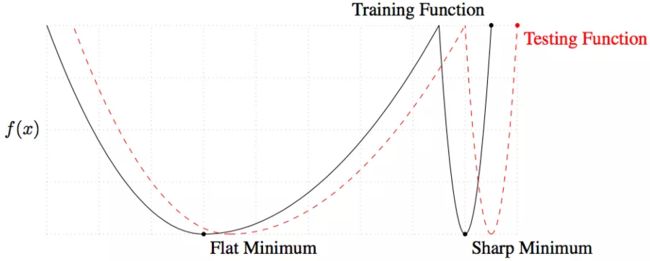
在理论上和实践中,Adam 系列的自适应学习率优化器都不善于寻找 flat minima,而 flat minima 对于 generalization 是很重要的。所以 Adam 的 training loss 可能更低,但 test performance 常常却更差。这是很多任务里避免用自适应学习率的最主要原因。同时,SGD 的理论基础较为明确、直观,而 以 Adam 为代表的自适应优化器是一种很 heuristic、理论机制不够清晰的方法。
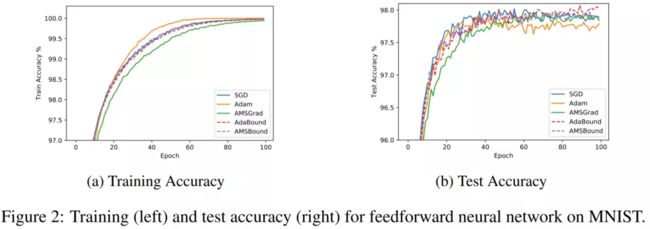
从以上两个实验对比容易看到,Adam 的 training 时确实收敛速度快,但在 testing 时造成的误差却都比 training 时差上许多。
事实上,在 CV 领域,SGD 系列时至今日仍是统治级的优化器。但是在 NLP (特别是 Transformer-based models) 领域,Adam 系列已最流行。所以为什么 SGD 和 Adam 会各有所长呢?
如果在 CV 中用 Adam 系列的自适应优化器,得到的结果很有可能会离 SGD 的 baseline 差好几个点。主要原因是,CV 任务的自适应优化器容易找到 sharp minima,泛化表现常常比 SGD 显著地差。如果训练 Transformer 模型,则 Adam 优化得更快且更好。主要原因是,NLP 任务的 loss landscape 有很多 “悬崖峭壁”,自适应学习率更能处理这种极端情况,避免梯度爆炸。基于同样的原因,CV 很少用的 gradient clipping 在 NLP 任务里几乎必不可少。(Why Gradient Clipping Accelerates Training: A Theoretical Justification for Adaptivity)。当然,也有一些例外。虽然 GAN 一般是 CV 任务,但 Adam 还是成为了最流行的优化器。主要原因是,GAN 的训练不太稳定,其 loss landscape 和正常的 CV 任务很不同。通常,能稳定训练 GAN 就足够好了,flat minima 对 GAN 的意义还不很明确。其实,对于比较极端的 loss landscape,Adam 可能会比较有优势。虽然 Adam 不擅长找到 flat minima,但 Adam 能比 SGD (有理论上保障地) 更快地逃离鞍点。
最后,很多人误以为 Adam 存在以下两个优点,但实际上并不存在。这也在一定程度上阻碍了 Adam 流行:
误解一,使用 Adam 无需调节初始学习率
尽管 Adam 默认的学习率 0.001 被广泛使用,但是在 Adam 比 SGD 表现好的领域,恰好都是重新调 Adam 的学习率的。比如训练 GAN 时大家一般用学习率 0.0002,而不是 0.001;而训练 Transformer 会需要比 0.001 更大的初始学习率,默认设置是学习率 0.2+ NOAM Scheduler。调节学习率对结果影响很大,可以说是优化器最重要的超参数。当然,Adam 在一般 CV 任务中无需调学习率,但是这些任务里无论调不调都无法匹敌 SGD。
误解二,使用 Adam 无需 learning rate decay
许多人甚至一些 PhD 和工程师对此也有很深误解。答案是,自适应优化器和 learning rate scheduler 经常需要同时 (叠加) 工作。SGD 和 Adam 的收敛性证明也都是要求 learning rate 最后会降到足够低的。但自适应优化器的学习率不会在训练中自动降到很低。实际上随便用 CIFAR 或 ImageNet 跑一跑常见模型就知道,训练的最后阶段,如果不主动把 learning rate 降下去,loss 根本就不会自己收敛到一个比较小的值,因此从理论到实践上都太需要 learning rate decay 了。
参考资料:
《百面机器学习》
https://mp.weixin.qq.com/s/-onwC8oxNHyeezEnSjHx3w
https://mp.weixin.qq.com/s/p5nYf5iWpevPpKotWpp6Og
https://mp.weixin.qq.com/s/RLzRI7DJMiVc9sZyBSAY1A
https://mp.weixin.qq.com/s/-onwC8oxNHyeezEnSjHx3w
https://mp.weixin.qq.com/s/bv65yqoaw35ZaGywxHGenw
Adam的问题与改善方案
SGD有多种改进的形式,为什么大多数论文中仍然用SGD?
SGD有多种改进的形式(RMSprop,Adadelta等),为什么大多数论文中仍然用SGD? - 知乎
https://www.cnblogs.com/peachtea/p/13532209.html
【python实现卷积神经网络】优化器的实现(SGD、Nesterov、Adagrad、Adadelta、RMSprop、Adam) - 走看看