动态规划:背包问题
文章目录
- **背包问题**
-
- 0 1 背包问题
-
- 时间复杂度 O ( n m ) O(nm) O(nm)
- 优化为一维
-
- **01背包问题空间优化的原理是:**
- 完全背包问题
-
- **朴素做法**
- **优化版本**
- **再度优化(一维)**
- 多重背包问题
-
- **朴素版**
- **优化版**
- 分组背包问题
- **python缩进**
背包问题
D P DP DP 从两个角度来考虑 : 状态表示 f ( i , j ) f ( i, j ) f(i,j) 与 状态计算
状态表示 f ( i , j ) f ( i, j ) f(i,j) 从 集合 和 属性 ( m a x , m i n , n u m ) ( max, min, num ) (max,min,num) 考虑
D P DP DP 优化一般是对动态规划的代码或者方程做一个等价变形
N N N 个物品 和一个容量是 V V V 的背包,每个物品有 2 2 2 个属性,一个是他的体积 v i v_{i} vi,还有个是他的价值 w i w_{i} wi
从集合角度考虑分为
- 所有选法
- 条件
- 只从前 i i i 个物品中选
- 总体积 < = j <= j <=j
f ( i , j ) f(i, j) f(i,j) 表示只从前 i i i 个物品中选并且总体积 ≤ j j j 的选法的集合,它存的数是里面每一个选法的总价值的最大值
–> f ( N , V ) f(N, V) f(N,V)
状态计算 对应 集合的划分

原则:
- 不重
- 不漏
不含 i i i : 1 ∼ i − 1 1 \sim i - 1 1∼i−1 即 f ( i − 1 , j ) f( i - 1 , j ) f(i−1,j)
含 i i i : 从 1 ∼ i − 1 1 \sim i - 1 1∼i−1 中选,且总体积不超过 j − v i j - v_{i} j−vi,即 f ( i − 1 , j − v i ) f ( i -1 , j - vi ) f(i−1,j−vi)
最后再加上第 i i i 个物品的价值 w i w_{i} wi,即 f ( i − 1 , j − v i ) + w i f ( i -1 , j - vi ) + wi f(i−1,j−vi)+wi
因此, f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i − 1 , j − v i ) + w i ) f ( i , j ) = max( f ( i - 1 , j ) , f ( i - 1 , j - vi ) + wi ) f(i,j)=max(f(i−1,j),f(i−1,j−vi)+wi)
0 1 背包问题
每件物品只能用一次 \textcolor{red}{每件物品只能用一次} 每件物品只能用一次,可以选择放或不放
f [ i ] [ v ] f[i][v] f[i][v] 表示前 i i i 件物品恰好放入一个容量为 v v v 的背包可以获得的最大价值
状态转移方程 f [ i ] [ v ] = m a x ( f [ i − 1 ] [ v ] , f [ i − 1 ] [ v − c [ i ] ] + w [ i ] ) f[i][v] = max(f[i-1][v], f[i - 1][v - c[i]] + w[i]) f[i][v]=max(f[i−1][v],f[i−1][v−c[i]]+w[i])
如果只考虑第 i i i 件物品放或不放,就可以转换成前关于 i − 1 i - 1 i−1 件物品的问题,如果不放第 i i i 件物品,那么就是前 i − 1 i - 1 i−1 件物品放入容量为 v v v 的背包种,价值为 f [ i − 1 ] [ v ] f[i - 1][v] f[i−1][v];如果放入第 i i i 件物品,那么就转换成前 i − 1 i - 1 i−1 件物品放入剩下的容量为 v − c [ i ] v - c[i] v−c[i] 的背包中,此时能获得的最大价值就是 f [ i − 1 ] [ v − c [ i ] ] + w [ i ] f[i- 1][v - c[i]] + w[i] f[i−1][v−c[i]]+w[i]
时间复杂度 O ( n m ) O(nm) O(nm)
#include优化为一维
因为 f [ i ] [ j ] = f [ i − 1 ] [ j ] ; f[i][j] = f[i - 1][j]; f[i][j]=f[i−1][j];
f [ i ] [ j ] = m a x ( f [ i ] [ j ] , f [ i − 1 ] [ j − v [ i ] ] + w [ i ] ) ; f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); f[i][j]=max(f[i][j],f[i−1][j−v[i]]+w[i]);
f ( i ) f(i) f(i) 只用到了 f ( i − 1 ) f( i - 1 ) f(i−1)
又因为 j − v i ≤ j j - vi ≤ j j−vi≤j
改成一维f表示
for(int i = 1; i <= n; i ++)
for(int j = v[i]; j <= m; j ++)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
f [ j ] = m a x ( f [ j ] , f [ j − v [ i ] ] + w [ i ] ) f[j] = max(f[j], f[j - v[i]] + w[i]) f[j]=max(f[j],f[j−v[i]]+w[i])
错误 \textcolor{red}{错误} 错误
如果顺序遍历的话 f [ j ] f[j] f[j] 会被前面的状态所影响。
因为 j − v [ i ] < j j - v[i] < j j−v[i]<j ,它已经在 f [ j ] f [ j ] f[j] 之前被计算过了,在第 i 层已经被计算,所以这样是等价于 f [ i ] [ j − v [ i ] ] + w [ i ] f[ i ] [ j - v[ i ]] + w[i] f[i][j−v[i]]+w[i]
但我们实际上应该是 f [ i − 1 ] [ j − v [ i ] ] + w [ i ] f[ i - 1 ] [ j - v[ i ]] + w[i] f[i−1][j−v[i]]+w[i]
应该让 j j j 倒着遍历
for(int i = 1; i <= n; i ++)
for(int j = m; j >= v[i]; j --)
{
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
让 j j j 倒着遍历,在计算 f [ j ] f[j] f[j] 时, f [ j − v [ i ] ] f[j - v[i]] f[j−v[i]] 还没有被更新过,所以存的是第 i − 1 i - 1 i−1 层的 j − v [ i ] j - v[i] j−v[i]
即这样才表示 f [ i ] [ j ] = m a x ( f [ i ] [ j ] , f [ i − 1 ] [ j − v [ i ] ] + w [ i ] ) f[i][j] = max(f[i][j], f[ i - 1 ] [ j - v[ i ]] + w[i]) f[i][j]=max(f[i][j],f[i−1][j−v[i]]+w[i])
01背包问题空间优化的原理是:
我们其实还是进行双重循环
-
外层for还是用来遍历原来二维数组的每一行(虽然现在已经没有二维数组了,但是表示的还是这个意义,只不过是用一维数组一直通过外层循环将每一行的值更新)
-
内层循环就是在更新二维数组(同上一个括号内的说法)的每一行中的每一列的值。
-
因此我们还想用上一行的值得时候,就不能从前往后了,要从后往前,更新某行最后一个值的时候,其实前面的值存储的还是上一行的所有值,所以不受影响。
完全背包问题
每件物品有无限个 \textcolor{red}{每件物品有无限个} 每件物品有无限个
状态表示 f [ i , j ] f [ i , j ] f[i,j] 集合:所有只考虑前 i i i 个物品,且总体积不大于 j j j 的所有选法
属性: M A X MAX MAX
状态计算
集合的划分
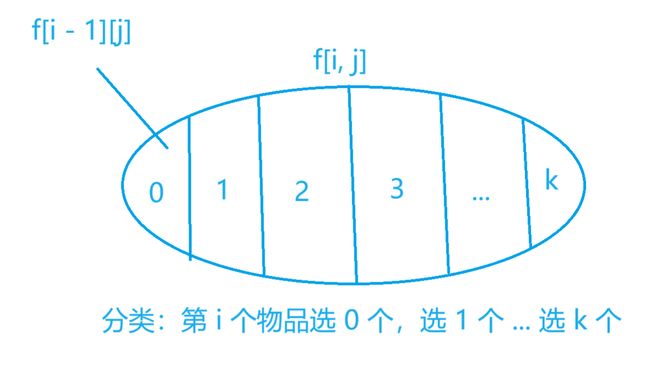
第 i i i 个物品选 0 0 0 个相当于从 i − 1 i - 1 i−1 个物品中选,相当于 f [ i − 1 ] [ j ] f[i - 1][j] f[i−1][j]
曲线救国
-
去掉 k k k 个物品 i i i
-
求 M A X MAX MAX, f [ i − 1 , j − k ∗ v [ i ] ] f [ i - 1 , j - k * v[ i ] ] f[i−1,j−k∗v[i]]
-
再加回来 k k k 个物品 i i i
--> f [ i − 1 , j − k ∗ v [ i ] ] + k ∗ w [ i ] f [ i - 1 , j - k * v[ i ] ] + k * w[ i ] f[i−1,j−k∗v[i]]+k∗w[i]
0 0 0:第 i i i 个物品选 0 0 0 个,相当于 f [ i − 1 , j ] f [ i - 1 , j ] f[i−1,j]
所以合在一起
就是 f [ i , j ] = f [ i − 1 , j − v [ i ] ∗ k ] + w [ i ] ∗ k f [ i , j ] = f [ i - 1 , j - v [ i ] * k ] + w [ i ] * k f[i,j]=f[i−1,j−v[i]∗k]+w[i]∗k
朴素做法
#include优化版本
f [ i , j ] = M a x ( f [ i − 1 , j ] , f [ i − 1 , j − v ] + w , f [ i − 1 , j − 2 v ] + 2 w , f [ i − 1 , j − 3 v ] + 3 w , . . . ) f[i,j] = Max(f[i - 1, j], f[i - 1, j - v] + w, f[i - 1, j - 2v] + 2w, f[i - 1, j - 3v] + 3w ,...) f[i,j]=Max(f[i−1,j],f[i−1,j−v]+w,f[i−1,j−2v]+2w,f[i−1,j−3v]+3w,...)
f [ i , j − v ] = M a x ( f [ i − 1 , j − v ] , f [ i − 1 , j − 2 v ] + w , f [ i − 1 , j − 3 v ] + 2 w , . . . ) f[i,j - v] = Max(~~~~~~~~~~~f[i - 1, j - v], f[i - 1, j - 2v] + w, f[i - 1, j - 3v] + 2w, ...) f[i,j−v]=Max( f[i−1,j−v],f[i−1,j−2v]+w,f[i−1,j−3v]+2w,...)
可以看出来第一条式子和第二条式子很相近

M a x ( f [ i − 1 , j − v ] + w , f [ i − 1 , j − 2 v ] + 2 w , f [ i − 1 , j − 3 v ] + 3 w , . . . ) = f [ i , j − v ] + w Max(f[i - 1, j - v] + w, f[i - 1, j - 2v] + 2w, f[i - 1, j - 3v] + 3w ,...) = f[i, j - v] + w Max(f[i−1,j−v]+w,f[i−1,j−2v]+2w,f[i−1,j−3v]+3w,...)=f[i,j−v]+w
所以
f [ i , j ] = M a x ( f [ i − 1 , j ] , f [ i , j − v ] + w ) f [ i , j ] = Max( f [ i - 1, j ], f [ i , j - v ] + w ) f[i,j]=Max(f[i−1,j],f[i,j−v]+w)
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i - 1][j];
if( j >= v[i])
f[i][j] = max( f[i][j], f[i][j - v[i]] + w[i] );
}
再度优化(一维)
f [ i , j ] = M a x ( f [ i , j ] , f [ i , j − v ] + w ) f [ i , j ] = Max( f [ i, j ], f [ i , j - v ] + w ) f[i,j]=Max(f[i,j],f[i,j−v]+w)
因为都是在第 i i i 层,所以可以直接删掉变成
f [ j ] = M a x ( f [ j ] , f [ j − v ] + w ) f [ j ] = Max( f [ j ], f [ j - v ] + w ) f[j]=Max(f[j],f[j−v]+w)
同时,因为是在第 i − 1 i - 1 i−1 层,所以 j j j 不用倒序
#include多重背包问题
每个物品最多有 s i 个 \textcolor{red}{每个物品最多有 si 个} 每个物品最多有si个

f [ i , j ] = M a x ( f [ i ] [ j ] , f [ i − 1 ] [ j − v [ i ] ∗ k ] + w [ i ] ∗ k ) f [ i , j ] = Max( f [ i ] [ j ] , f [ i - 1 ] [ j - v [ i ] * k ] + w [ i ] * k ) f[i,j]=Max(f[i][j],f[i−1][j−v[i]∗k]+w[i]∗k)
其中 k = 0 , 1 , 2 , . . . , s [ i ] k = 0, 1, 2, ... , s[ i ] k=0,1,2,...,s[i]
朴素版
#include优化版
f [ i , j ] = m a x ( f [ i − 1 , j ] , f [ i − 1 , j − v ] + w , f [ i − 1 , j − 2 v ] + 2 w , . . . , f [ i − 1 , j − s v ] + s w ) f[i,j] = max(f[i-1,j],f[i-1,j-v]+w,f[i-1,j-2v]+2w,...,f[i-1,j-sv]+sw) f[i,j]=max(f[i−1,j],f[i−1,j−v]+w,f[i−1,j−2v]+2w,...,f[i−1,j−sv]+sw)
f [ i , j − v ] = m a x ( f [ i − 1 , j − v ] , f [ i − 1 , j − 2 v ] + w , f [ i − 1 , j − 3 v ] + 2 w , . . . , f [ i − 1 , j − s v ] + s w ) f[i,j-v] = max(~~~~~~~~~~~f[i-1,j-v],f[i-1,j-2v]+w,f[i-1,j-3v]+2w,...,f[i-1,j-sv]+sw) f[i,j−v]=max( f[i−1,j−v],f[i−1,j−2v]+w,f[i−1,j−3v]+2w,...,f[i−1,j−sv]+sw)
无法直接优化
可以用 二进制优化
s = 1023 s = 1023 s=1023
0 , 1 , 2 , . . . , 1023 0, 1, 2, ... , 1023 0,1,2,...,1023
–> $1, 2, 4, 8, … , 512 $
用 1 1 1 可以凑出来 $0 ~ 1 $
加上 2 2 2 可以凑出来 0 3 0 ~ 3 0 3
加上 4 4 4 可以凑出来 0 ∼ 7 0 \sim 7 0∼7
…
加到 512 512 512 可以凑出来 0 ∼ 1023 0 \sim 1023 0∼1023
用 10 个新的物品来表示原来的第 i i i个物品
–> O ( l o g n ) O( logn ) O(logn)
s = 200 s = 200 s=200
$1, 2, 4, 8, 16, 32, 64, 73 $
对于 s s s ,可以分为 1 , 2 , 4 , 8 , . . . , 2 k 1,2,4,8,...,2^k 1,2,4,8,...,2k, c ( c < 2 k + 1 ) c ( c < 2^{k + 1}) c(c<2k+1)
$1 \sim 2^k $ 可以凑出来 $0 \sim 2 ^{k + 1} - 1 $
加上 c c c 后 就可以凑出来 $0 \sim 2 ^{k + 1} - 1 + c $ 也就是 $0 \sim s $
先将 s i s_{i} si 拆分成 l o g ( s i ) log( s_{i} ) log(si) 个
O ( n × v × s ) − − > O ( n × v × l o g ( s ) ) O( n \times v \times s ) --> O( n \times v \times log(s) ) O(n×v×s)−−>O(n×v×log(s))
#include分组背包问题
有 N 组,每一组物品里面有若干个 \textcolor{red}{有 N 组,每一组物品里面有若干个} 有N组,每一组物品里面有若干个
每一组里面最多只能选一种物品 \textcolor{red}{每一组里面最多只能选一种物品} 每一组里面最多只能选一种物品
状态表示 f [ i , j ] f [ i, j ] f[i,j]
冬重背包问题是枚举第 i i i 个物品选几个,分组背包问题是枚举第 i i i 组物品选哪个或者不选

第一种表示第 i i i 组物品一个都不选 就是相当于 f [ i − 1 , j ] f [ i - 1 , j ] f[i−1,j]
对于中间的某一个,从第 i i i 组物品中选择 k k k 个物品 f [ i − 1 , j − v [ i , k ] ] + w [ i , k ] f [ i - 1, j - v[ i , k] ] + w[ i, k ] f[i−1,j−v[i,k]]+w[i,k]
#includepython缩进
时空限制 1 s / 256 M B 1s / 256 MB 1s/256MB
动态规划:
状态表示 f ( i , j ) f(i, j) f(i,j)
集合:所有由前 i i i 条语句构成,且第 i i i 条语句缩进了 j j j 级的所有方案的集合。
属性:方案数
状态计算
上一条如果是 for 循环,不管后面是 for 还是 普通语句,都比上一条多一级,如果该条语句在第 j j j 级,则上一条在第 j − 1 j - 1 j−1 级
f ( i , j ) = f ( i − 1 , j − 1 ) f(i, j) = f(i - 1, j - 1) f(i,j)=f(i−1,j−1)
上一条如果是普通语句,
f ( i , j ) = f ( i − 1 , j ) + f ( i − 1 , j + 1 ) + . . . + f ( i − 1 , i − 2 ) f(i, j) = f(i - 1, j) + f(i - 1, j + 1) + ... + f(i - 1, i -2) f(i,j)=f(i−1,j)+f(i−1,j+1)+...+f(i−1,i−2)
因为
f ( i , j + 1 ) = f ( i − 1 , j + 1 ) + f ( i − 1 , j + 2 ) + . . . + f ( i − 1 , i − 2 ) f(i, j + 1) = f(i - 1, j + 1) + f(i - 1, j + 2) + ... + f(i - 1, i -2) f(i,j+1)=f(i−1,j+1)+f(i−1,j+2)+...+f(i−1,i−2)
所以
f ( i , j ) = f ( i − 1 , j ) + f ( i , j + 1 ) f(i, j) = f(i - 1, j) + f(i, j + 1) f(i,j)=f(i−1,j)+f(i,j+1)
#include