最小生成树--kruskal算法（并查集+贪心）

忘了定义的来复习一下吧：树是指没有环的连通无向图（这样的树也叫无向树）。生成树是指连通无向图的极小（极小是指边数目最小）连通子图。最小生成树，就是对于一个加权图来说，所有生成树中边的权值之和最小的那一个。显然，n个顶点的图，生成树有n-1条边。我们先说一个重要定理（有兴趣的自己去看证明）：
一个无向图的最小生成树。必然包含权值最小的边；必然不包含环路中权值最大的边（或者至少有一条这样的边不被包含）。
什么意思呢？

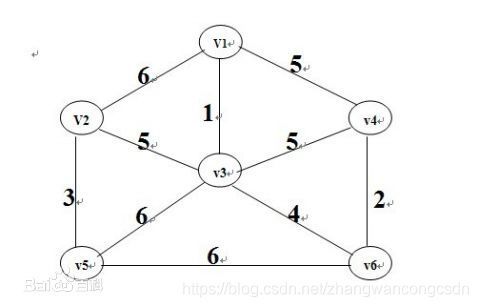
比如上图，它的最小生成树必然包含边1，不能同时包含三个6。

最小生成树有两个非常漂亮的算法：prim算法和kruskal算法。我们今天来讨论后者。
它的基本思想就是：每次选取不成环的最小边，直到选出n-1条边。这是贪心思想，每次只取当前最小。
比如上图，先选1（想一下上面的定理，第一步为什么是对的）。然后是2、3、4，都不成环。

选到5的时候，要注意了，有两条权值为5的边是成环的。所以只能选取v2和v3之间的边。
发现这时已经选了5条边，已经是最小生成树。所以，最小权值之和为15。
问题的关键就在于，在算法实现中如何选取不成环的边呢？
有些算法看起来简单，实际上想要彻底理解还需要一番功夫。

查找最小边比较简单，把边集存储下来，排序，每次找最小。但是判断成环就比较麻烦了，要检查这条边连接的两个点是否在一个连通分量中。（如果两者在同一连通分量，直接连接必然成环）。如何判断呢？

答案就是并查集（union-find set）。顾名思义，就是快速查询和合并。并查集不支持删除。

我们可以这样想，选取一条边，那么这两个顶点就是“父子”关系。这样的关系绝对不成环（乱伦哈哈哈）对吧，所以每次选取一条边，它两个顶点所在的两个不同的并查集就形成父子关系。如果它们在同一并查集中，那这条边就不予考虑。
我们可以用一个数组father[]来表示图的并查集。数组的下标就是顶点编号，内容就是这个顶点的“父亲”。如果内容为负数说明它是“祖先”。这就是一个树形结构。
合并也很简单，把某个顶点的father[i]改成它的“父亲”，O(1)时间。

回到刚才的图，我们先开始选取的1,2,3,三条边，它们形成三棵树（马上住，滑稽~）。
v1—v3
v2—v5
v6—v4（我故意4、6反过来写，待会就会发现这里有优化的地方）

然后选取4的时候，有两棵树被合并了。
v1—v3—v6—v4
v2—v5

再选取边，1-3和3-4已经在一个并查集中，不能再选。
判断两个顶点是否在一个并查集就很简单了。因为每一个并查集只有一个“祖先”，所以要有一个“寻根函数”root()。它是一个递归函数，如果father[i]是负数就返回 i 本身，否则返回 root(father[i])。如果两个顶点的root值相等，那就表明它们在同一并查集。

int root(int x)
{
    if(father[x]<0) return x;
    else return root(father[x]);
}

看起来完成了，但是真的完成了？

精益求精嘛，刚才看到，合并v1—v3 和 v6—v4两棵树的时候，树的深度达到了4。如果并查集的规模再大一点，比如100万，那就是“退化树”，相当于一个100万长度的链表。如果要查找两个顶点是否在一个并查集，平均查找长度达到了O(n)。这显然是不可接受的。

为了解决这个问题，我们再次用到寻根函数。每次合并时，把两个并查集的“祖先”形成父子（这回不能叫父子了，应该叫长幼哈哈）。反正并查集不考虑具体连接关系，只要能表示连通分量即可。这样，每次合并后，就大大缩短了树的深度。

比如刚才的v1—v3和v6—v4，祖先分别为1和6。那么我们就合并成
v1—v6—v4
|
v3

这样深度就是3了。别小看减少一层，如果多次合并，可是减小成千上万层的。

那还能不能优化呢？能！合并的时候，我们说把两个祖先形成父子，那么谁当爸爸呢？当然是牛B的一方当爸爸了！什么意思呢？谁的深度大，谁当爸爸。
骚年，你深度不够，你只配做我儿子~

如果刚才是v1—v3（深度为2）和v6—v4—v5（深度为3）的话，我们看两种情况
v1—v6—v4—v5 （深度为4）
|
v3

v6—v4—v5 （深度为3）
|
v1
|
v3

所以当然是深度大的当爸爸，这样就可以保持整个并查集的深度最小。

那如何表示深度呢？注意到刚才说的“祖先”的father[i]是负数了吧，我们可以利用它，用它的绝对值来表示以它为根的并查集的深度（负数比较大小的时候要千万注意，注意，注意！重要的事情说三遍）。假设将要合并的两个根的深度分别为d1,d2（d1换成father值，也就是d1,d2的相反数，就是father[1]>father[2]），合并的时候，d2将要“当爸爸”，成为新的并查集的根，它的深度就是max{d2 , d1+1}，father就是min{ father[2] , father[1]-1 }。

合并函数也出来了：

inline int Min(int x,int y)
{
    return x<y?x:y;
}
bool Merge(int x,int y)
{
    x=root(x);
    y=root(y);
    if(x==y) return false;//在同一并查集中，合并失败
    if(father[x]>father[y])
        father[y]=Min(father[x]-1,father[y]),father[x]=y;
        //deep(x)
        //注意两个不能写反，想想为什么
    else
        father[x]=Min(father[y]-1,father[x]),father[y]=x;
    return true;
}

一开始都是单个结点，所以都是祖先，深度都为1。把它们都赋初始值-1。
最后考虑图的存储。因为kruskal算法只考虑边，结点仅仅用于判断成环，所以邻接矩阵和邻接表都是多余的。只需要存储边集合。边要表示出权值和所连接的两顶点。

例题：一个v(2<=v<=10000)台计算机组成的阵列，编号为1~v，需要连成局域网。有e(1<=e<=600000)个可能的连接，每个连接能连通两台计算机i，j（i,j<=v），需要成本price(int范围内)。现在要保证这v台计算机都在一个局域网中，求满足这样条件的最小成本。没有自环，可能有重边。
输入：e+1行。第一行为两个正整数v，e。接下来e行，每行三个正整数 i j price，含义见题目描述。
输出：一行，为最小成本。
时间限制：1000ms 内存限制：64MB

贴上完整代码

#include
#include
#include
#include
using namespace std;
typedef struct
{
    int v1;
    int v2;
    int weight;
}edge;
edge elist[600000];
int father[10001];
int cmp(edge a,edge b)
{
    return a.weight<b.weight;
}
int root(int x)
{
    if(father[x]<0) return x;
    else return root(father[x]);
}
inline int Min(int x,int y)
{
    return x<y?x:y;
}
bool Merge(int x,int y)
{
    x=root(x);
    y=root(y);
    if(x==y) return false;
    if(father[x]>father[y])
        father[y]=Min(father[x]-1,father[y]),father[x]=y;
    else
        father[x]=Min(father[y]-1,father[x]),father[y]=x;
    return true;
}
int main(int argc,char *argv[])
{
    int v,e,i,cnt=0;
    long long totalw=0;
    scanf("%d %d",&v,&e);
    for(i=0;i<e;i++)
        scanf("%d %d %d",&elist[i].v1,&elist[i].v2,&elist[i].weight);
    sort(elist,elist+e,cmp);
    memset(father,-1,sizeof(father));
    i=0;
    while(cnt<v-1)
    {
        if(Merge(elist[i].v1,elist[i].v2))
            totalw+=(long long)elist[i].weight,cnt++;
        i++;
    }
    printf("%lld\n",totalw);
    return 0;
}

小长假最后一天，2019撸起袖子加油干，我们都是追梦人！