【机器学习】强化学习（三）蒙特卡洛算法

策略迭代算法和价值迭代算法为什么可以得到理论上的最优解，在实际问题中使用价值有限？

无模型算法

三、蒙特卡洛算法

蒙特卡洛(Monte Carlo)方法是一种基于样本的强化学习算法，它通过执行和学习代理（也就是我们编程的AI）环境交互的样本路径来学习。它不需要初始知识的模型，只依赖样本结果。蒙特卡洛算法主要用于求解策略估计和控制问题。对于复杂的问题，通过采样方法，我们可以获得近似解。这就是为什么蒙特卡洛方法在强化学习中被广泛使用。

具体来说，蒙特卡洛方法在强化学习中有两个主要应用：策略评估和控制。策略评估指的是估计一个已知策略的价值函数。然而，控制则试图找出最佳策略。

首先，对于策略评估，我们对一系列由特定策略生成的轨迹进行样本平均。然后，我们利用这些经验平均值来估计价值函数。

其次，蒙特卡洛控制使用了一种“策略迭代”的思想，通过交替进行策略评估和策略改进，直到找出最佳策略。这个方法的一个重要积极性就是它不需要环境的完全模型。

蒙特卡洛方法的一个主要优点是它能够处理连续和离散的环境，因此在实际问题中具有很高的应用价值。

3.1 算法简介

蒙特卡洛算法估计圆周率pi动画 python实现

# 导入随机数、日期时间、绘图和数值计算的模块
import random
from datetime import datetime


import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera # 用于创建动画的模块
from matplotlib.gridspec import GridSpec # 用于设置子图的布局的模块
from tqdm import tqdm # 用于显示进度条的模块


# 常量
RADIUS = 1  # 圆的半径
LENGTH = 2 * RADIUS  # 正方形的边长
AREA_SQUARE = LENGTH ** 2  # 正方形的面积
AREA_CIRCLE = np.pi * RADIUS ** 2  # 圆的面积
NUM_ITER = 10000  # 随机生成的点的个数
NUM_CHECKPOINTS = 100  # 动画的快照的个数
CHECKPOINT_ITER = NUM_ITER // NUM_CHECKPOINTS # 每个快照之间的间隔


# 子图的索引
MAIN = 0
ESTIMATE = 1
ACC_OVER_TIME = 2




def generate_point() -> np.ndarray:
    """
    在正方形内随机生成一个点，
    返回点的坐标
    """
    return np.array([random.random() * LENGTH-1, random.random() * LENGTH-1]) # 生成一个在[-1,1)之间的随机数作为x坐标和y坐标




def is_point_in_circle(point: np.ndarray) -> bool:
    """
    给定一个`point`，返回它是否在圆内
    """
    return point[0] ** 2 + point[1] ** 2 < RADIUS ** 2 # 如果点到圆心的距离小于半径，即在圆内，返回True，否则返回False




def setup_plot() -> (plt.axes, plt.axes, plt.axes, plt.figure):
    """
    设置初始的图形。返回三个子图和一个图形对象。
    """
    fig = plt.gcf() # 获取当前的图形对象
    gs = GridSpec(3, 3) # 创建一个3行3列的网格布局
    ax_main = fig.add_subplot(gs[0:2, 0:2])  # 主要的子图，显示圆和正方形
    ax_estimate = fig.add_subplot(gs[0, 2])  # 显示当前估计值的子图
    ax_acc_time = fig.add_subplot(gs[2, :])  # 显示估计值随时间变化的子图


    # 图形的属性
    fig.set_size_inches(10, 10) # 设置图形的大小为10英寸乘10英寸


    # 主要子图的属性
    ax_main.grid() # 显示网格线
    ax_main.set_xlim([-1.1, 1.1]) # 设置x轴的范围为[-1.1, 1.1]
    ax_main.set_ylim([-1.1, 1.1]) # 设置y轴的范围为[-1.1, 1.1]
    ax_main.set_title("Espimating Pi using Monte Carlo Methods") # 设置子图的标题


    # 估计值子图的属性
    ax_estimate.axis("off") # 关闭坐标轴
    ax_estimate.set_title("Current Estimate") # 设置子图的标题


    # 估计值随时间变化子图的属性
    ax_acc_time.set_xlim([0, NUM_ITER]) # 设置x轴的范围为[0, NUM_ITER]
    ax_acc_time.set_ylim([np.pi - 0.2, np.pi + 0.2]) # 设置y轴的范围为[np.pi - 0.2, np.pi + 0.2]
    ax_acc_time.hlines(y=np.pi, xmin=0, xmax=NUM_ITER, colors="b") # 用蓝色的水平线绘制真实的圆周率值
    ax_acc_time.grid() # 显示网格线
    ax_acc_time.set_title("Estimate over time") # 设置子图的标题


    return (ax_main, ax_estimate, ax_acc_time), fig # 返回三个子图和一个图形对象




def update_main_axes(axes: plt.axes, inside_circle: np.ndarray,
                     outside_circle: np.ndarray, circle: plt.Circle,
                     square: plt.Rectangle) -> None:
    """
    在拍摄快照之前，用新的信息更新主要的子图。
    """
    axes.scatter(*(outside_circle.T), c="red", marker='.') # 用红色的点绘制圆外的点的坐标
    axes.scatter(*(inside_circle.T), c="green", marker='.') # 用绿色的点绘制圆内的点的坐标
    axes.add_artist(circle) # 将圆对象添加到子图中
    axes.add_artist(square) # 将正方形对象添加到子图中




def update_estimate_axes(axes: plt.axes, num_in_circle: int,
                         current_iter: int) -> float:
    """
    在拍摄快照之前，用新的信息更新估计值的子图。
    """
    pi_est = estimate_pi(num_in_circle, current_iter) # 根据圆内的点的数量和总的点的数量，计算圆周率的估计值
    pi_formatted = f"{pi_est:.5f}" # 将圆周率的估计值格式化为保留5位小数的字符串
    current_iter_formatted = f"Current iteration: {current_iter - 1}" # 将当前的迭代次数格式化为字符串
    num_in_circle_formatted = f"Points inside circle: {num_in_circle}" # 将圆内的点的数量格式化为字符串
    num_out_circle_formatted = f"Points outside circle: {current_iter - num_in_circle}" # 将圆外的点的数量格式化为字符串
    error = np.abs(np.pi - pi_est) # 计算圆周率的估计值和真实值的绝对误差
    error_formatted = f"Error: {error:.5f}" # 将误差格式化为保留5位小数的字符串
    percent_error = error / np.pi * 100 # 计算圆周率的估计值和真实值的相对误差百分比
    percent_error_formatted = f"Relative error: {percent_error:.5f}%" # 将百分比格式化为保留5位小数的字符串


    axes.text(0, 0.7, pi_formatted, size=40, bbox={"facecolor": "b", "alpha": 0.5}) # 在子图中显示圆周率的估计值，字体大小为40，背景颜色为蓝色，透明度为0.5
    axes.text(0, 0.4, current_iter_formatted, size=15) # 在子图中显示当前的迭代次数，字体大小为15
    axes.text(0, 0.25, num_in_circle_formatted, size=15) # 在子图中显示圆内的点的数量，字体大小为15
    axes.text(0, 0.1, num_out_circle_formatted, size=15) # 在子图中显示圆外的点的数量，字体大小为15
    axes.text(0, -0.05, error_formatted, size=15) # 在子图中显示误差，字体大小为15
    axes.text(0, -0.2, percent_error_formatted, size=15) # 在子图中显示百分比，字体大小为15


    return pi_est # 返回圆周率的估计值


# 定义一个函数，用于更新估计值随时间变化的子图
def update_acc_time_axes(axes: plt.axes, estimates: [float]) -> None:
    """
    在拍摄快照之前，用新的信息更新估计值随时间变化的子图。
    """
    axes.hlines(y=np.pi, xmin=0, xmax=NUM_ITER, colors="b") # 用蓝色的水平线绘制真实的圆周率值
    axes.plot(
        range(0, CHECKPOINT_ITER * len(estimates), CHECKPOINT_ITER), # 用橙色的线绘制每个快照时的估计值
        estimates, color="orange")




# 定义一个函数，用于根据圆内的点的数量和总的点的数量，计算圆周率的估计值
def estimate_pi(num_in_circle: int, current_iter: int) -> float:
    """
    给定`num_in_circle`，返回当前的圆周率的估计值。
    """
    return num_in_circle / current_iter * AREA_SQUARE # 用圆内的点的数量除以总的点的数量，再乘以正方形的面积，得到圆周率的估计值




# 如果是主程序
if __name__ == "__main__":
    random.seed(datetime.now()) # 用当前的日期时间作为随机数的种子
    points_inside_circle = np.full((NUM_ITER, 2), np.nan) # 创建一个NUM_ITER行2列的数组，用于存储圆内的点的坐标，初始值为nan
    points_outside_circle = np.full((NUM_ITER, 2), np.nan) # 创建一个NUM_ITER行2列的数组，用于存储圆外的点的坐标，初始值为nan
    estimates = [] # 创建一个空列表，用于存储每个快照时的圆周率的估计值


    # 设置图形
    axes, fig = setup_plot() # 调用setup_plot函数，返回三个子图和一个图形对象
    camera = Camera(fig) # 创建一个相机对象，用于拍摄图形的快照


    # 添加初始的圆和正方形
    circle = plt.Circle((0, 0), radius=RADIUS, color='g', fill=False) # 创建一个圆心为(0,0)，半径为RADIUS，颜色为绿色，不填充的圆对象
    rect = plt.Rectangle((-1, -1), 2, 2, color='r', fill=False) # 创建一个左下角为(-1,-1)，宽高为2，颜色为红色，不填充的正方形对象
    axes[MAIN].add_artist(circle) # 将圆对象添加到主要的子图中
    axes[MAIN].add_artist(rect) # 将正方形对象添加到主要的子图中


    # 投掷飞镖
    num_in_circle = 0 # 初始化圆内的点的数量为0
    num_outside_circle = 0 # 初始化圆外的点的数量为0
    for i in tqdm(range(NUM_ITER)): # 循环NUM_ITER次，显示进度条
        point = generate_point() # 调用generate_point函数，随机生成一个点
        if is_point_in_circle(point): # 如果点在圆内
            points_inside_circle[num_in_circle] = point # 将点的坐标存储到圆内的点的数组中
            num_in_circle += 1 # 圆内的点的数量加1
        else: # 如果点在圆外
            points_outside_circle[num_outside_circle] = point # 将点的坐标存储到圆外的点的数组中
            num_outside_circle += 1 # 圆外的点的数量加1
        # 定期拍摄快照
        if i % CHECKPOINT_ITER == 0: # 如果是每个快照的间隔
            update_main_axes(axes[MAIN], points_inside_circle, # 调用update_main_axes函数，更新主要的子图
                             points_outside_circle, circle, rect)
            estimates.append( # 将当前的圆周率的估计值添加到列表中
                update_estimate_axes(axes[ESTIMATE], num_in_circle, i+1) # 调用update_estimate_axes函数，更新估计值的子图，返回当前的圆周率的估计值
                )
            update_acc_time_axes(axes[ACC_OVER_TIME], estimates) # 调用update_acc_time_axes函数，更新估计值随时间变化的子图
            camera.snap() # 拍摄图形的快照


    # 显示动画
    anim = camera.animate() # 用相机对象创建一个动画对象
    # 在显示动画之前保存动画，因为
    # https://github.com/matplotlib/matplotlib/issues/10287
    anim.save("animation.mp4") # 保存动画为视频文件
    plt.show() # 显示图形


    # 结果
    print("Number of points inside the circle:", num_in_circle) # 打印圆内的点的数量
    print("Number of points outside the circle:", num_outside_circle) # 打印圆外的点的数量
    print("Final PI estimate:", estimate_pi(num_in_circle, NUM_ITER)) # 打印最终的圆周率的估计值
    print("Read Value of PI:", np.pi) # 打印真实的圆周率的值
    
 输出：
DeprecationWarning: Seeding based on hashing is deprecated
since Python 3.9 and will be removed in a subsequent version. The only
supported seed types are: None, int, float, str, bytes, and bytearray.
  random.seed(datetime.now())
100%|████████████████████████████████████████████████████| 10000/10000 [00:00<00:00, 15407.67it/s]
Number of points inside the circle: 7797
Number of points outside the circle: 2203
Final PI estimate: 3.1188
Read Value of PI: 3.141592653589793

3.2 状态价值函数估计

蒙特卡洛策略评估算法是一种用于估计给定策略下的状态价值函数的算法。它的基本思想是通过采样大量的轨迹来计算每个状态的平均回报，然后用这个平均回报作为状态的价值。蒙特卡洛策略评估算法可以分为两种类型：首次访问和每次访问。

3.3 动作价值函数估计

3.4 蒙特卡洛控制

蒙特卡洛控制是一种用于寻找最优策略的算法，它结合了蒙特卡洛策略评估和策略改进的思想。蒙特卡洛控制的基本思想是通过不断地生成轨迹来更新状态-动作价值函数，并根据状态-动作价值函数来更新策略，使其趋向于贪婪策略。蒙特卡洛控制可以分为两种类型：探索启发式和探索-利用平衡。

3.5 应用

3.6 示例

示例1-用蒙特卡罗方法估计欧式看涨期权的价格，并用图形界面展示结果。

这个示例是一个用Python编写的程序，它可以用蒙特卡罗方法估计欧式看涨期权的价格，并用图形界面展示结果。期权是一种金融衍生品，它给予买方在未来以特定价格买入或卖出某种资产的权利。欧式看涨期权是一种最常见的期权，它给予买方在到期日以行权价买入一定数量的股票的权利。蒙特卡罗方法是一种用随机数模拟复杂问题的数值方法，它可以用来估计期权的价格。图形界面是一种让用户与程序交互的方式，它可以用图形元素如按钮、标签、输入框等来显示信息和接收输入。

这个示例的程序分为以下几个部分：

1. 首先，导入数值计算、图形界面、绘图的模块，这些模块提供了一些常用的函数和类，可以方便地进行数学运算、创建图形界面、绘制图表等。

2. 然后，定义一个函数，用于执行蒙特卡罗模拟计算期权价格。这个函数的输入参数有股票价格、行权价、到期时间、无风险利率、波动率、模拟次数等，它的输出是期权的价格。

3. 接着，定义一个函数，用于计算和显示期权价格的分布。

4. 最后，创建主窗口，设置主窗口的标题为“Monte Carlo Options Pricer”，为输入参数创建标签和输入框，显示输入参数的名称，接收用户的输入，创建一个按钮，用于计算期权价格并显示分布，绑定前面定义的函数，当用户点击时执行该函数，创建一个标签，用于显示计算出的期权价格，启动图形界面的主循环，让图形界面持续显示。

# 导入数值计算、图形界面、绘图的模块
import numpy as np
import tkinter as tk
from tkinter import ttk
import matplotlib.pyplot as plt
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg


# 定义一个函数，用于执行蒙特卡罗模拟计算期权价格
def monte_carlo_option_pricer(stock_price, strike_price, time_to_maturity, risk_free_rate, volatility, num_simulations):
    dt = time_to_maturity / 365 # 计算每天的时间间隔
    num_days = int(time_to_maturity) # 计算到期日的天数


    option_payoffs = [] # 创建一个空列表，用于存储期权的收益
    for _ in range(num_simulations): # 循环num_simulations次，模拟股票价格的变化
        stock_prices = [stock_price] # 创建一个列表，用于存储股票价格的路径，初始值为stock_price
        for _ in range(num_days): # 循环num_days次，模拟每天的股票价格
            z = np.random.normal()  # 用正态分布生成一个随机数
            price_movement = stock_prices[-1] * np.exp((risk_free_rate - 0.5 * volatility**2) * dt + volatility * np.sqrt(dt) * z) # 用几何布朗运动模型计算股票价格的变动
            stock_prices.append(price_movement) # 将股票价格的变动添加到股票价格的路径中


        option_payoff = max(0, stock_prices[-1] - strike_price) # 计算期权的收益，如果股票价格高于行权价，就执行期权，否则就放弃期权
        option_payoffs.append(option_payoff) # 将期权的收益添加到期权的收益的列表中


    option_price = np.exp(-risk_free_rate * time_to_maturity) * np.mean(option_payoffs) # 用期权的收益的平均值乘以贴现因子，得到期权的价格
    return option_price # 返回期权的价格




# 定义一个函数，用于计算和显示期权价格的分布
def calculate_option_price():
    try:
        # 从用户的输入中获取参数的值
        stock_price = float(stock_price_var.get()) # 获取股票价格的值，转换为浮点数
        strike_price = float(strike_price_var.get()) # 获取行权价的值，转换为浮点数
        time_to_maturity = float(time_to_maturity_var.get()) # 获取到期时间的值，转换为浮点数
        risk_free_rate = float(risk_free_rate_var.get()) # 获取无风险利率的值，转换为浮点数
        volatility = float(volatility_var.get()) # 获取波动率的值，转换为浮点数
        num_simulations = int(num_simulations_var.get()) # 获取模拟次数的值，转换为整数


        option_prices = [] # 创建一个空列表，用于存储期权价格的模拟结果
        for _ in range(1000):  # 循环1000次，模拟期权价格，用于绘制图表
            option_price = monte_carlo_option_pricer(stock_price, strike_price, time_to_maturity, risk_free_rate, volatility, num_simulations) # 调用monte_carlo_option_pricer函数，计算期权价格
            option_prices.append(option_price) # 将期权价格添加到期权价格的列表中


        average_option_price = np.mean(option_prices) # 计算期权价格的平均值
        option_price_label.config(text=f"Monte Carlo Option Price: {average_option_price:.4f}") # 在图形界面中显示期权价格的平均值，保留4位小数


        # 创建并显示一个柱状图
        plt.figure(figsize=(8, 5)) # 创建一个图形对象，大小为8英寸乘5英寸
        plt.hist(option_prices, bins=30, alpha=0.7, color='blue') # 用蓝色的柱状图绘制期权价格的分布，分成30个区间，透明度为0.7
        plt.axvline(x=average_option_price, color='red', linestyle='dashed', linewidth=2) # 用红色的虚线绘制期权价格的平均值
        plt.xlabel("Option Price") # 设置x轴的标签为“Option Price”
        plt.ylabel("Frequency") # 设置y轴的标签为“Frequency”
        plt.title("Option Price Distribution") # 设置图形的标题为“Option Price Distribution”
        plt.grid(True) # 显示网格线
        plt.tight_layout() # 调整图形的布局，避免重叠


        # 将图形嵌入到图形界面中
        canvas = FigureCanvasTkAgg(plt.gcf(), master=root) # 创建一个画布对象，将图形对象绘制在图形界面的主窗口上
        canvas_widget = canvas.get_tk_widget() # 获取画布对象的控件
        canvas_widget.grid(row=len(input_labels) + 2, columnspan=2) # 将画布对象的控件放置在图形界面的合适位置


    except ValueError: # 如果用户的输入不是有效的数值，抛出异常
        option_price_label.config(text="Invalid input. Please enter numeric values.") # 在图形界面中显示错误信息


# 创建主窗口
root = tk.Tk() # 创建一个Tkinter对象
root.title("Monte Carlo Options Pricer") # 设置主窗口的标题为“Monte Carlo Options Pricer”


# 为输入参数创建标签和输入框
input_labels = ["Stock Price:", "Strike Price:", "Time to Maturity (years):", "Risk-Free Rate:", "Volatility:", "Number of Simulations:"] # 创建一个列表，存储输入参数的标签
entry_vars = [] # 创建一个空列表，用于存储输入参数的变量


default_values = [100, 100, 1, 0.05, 0.3, 10000] # 创建一个列表，存储输入参数的默认值


for row, (label_text, default_value) in enumerate(zip(input_labels, default_values)): # 循环遍历输入参数的标签和默认值
    ttk.Label(root, text=label_text).grid(row=row, column=0) # 在图形界面中创建一个标签，显示输入参数的名称，放置在合适的位置
    entry_var = tk.StringVar(value=default_value) # 创建一个字符串变量，存储输入参数的值，初始值为默认值
    entry = ttk.Entry(root, textvariable=entry_var) # 在图形界面中创建一个输入框，绑定输入参数的变量，接收用户的输入
    entry.grid(row=row, column=1) # 将输入框放置在合适的位置
    entry_vars.append(entry_var) # 将输入参数的变量添加到列表中


stock_price_var, strike_price_var, time_to_maturity_var, risk_free_rate_var, volatility_var, num_simulations_var = entry_vars # 将输入参数的变量分别赋值给对应的变量名


# 创建一个按钮，用于计算期权价格并显示分布
calculate_button = ttk.Button(root, text="Calculate", command=calculate_option_price) # 在图形界面中创建一个按钮，显示“Calculate”，绑定calculate_option_price函数，当用户点击时执行该函数
calculate_button.grid(row=len(input_labels), columnspan=2) # 将按钮放置在合适的位置


# 创建一个标签，用于显示计算出的期权价格
option_price_label = ttk.Label(root, text="") # 在图形界面中创建一个标签，初始为空
option_price_label.grid(row=len(input_labels) + 1, columnspan=2) # 将标签放置在合适的位置


# 启动图形界面的主循环
root.mainloop() # 调用mainloop方法，让图形界面持续显示

输出结果：

截图是一个蒙特卡罗期权定价器的图形界面，它显示了基于给定参数的期权价格分布

• 期权价格的平均值是0.6024，这是用蒙特卡罗方法模拟了10000次股票价格的变化后，计算出的期权的价格的期望值。

• 期权价格的分布呈现一个近似正态分布的形状，这说明期权价格的变化受到随机因素的影响，但是也有一定的规律性。

• 期权价格的分布的标准差大约是0.01，这表示期权价格的波动程度不是很大，大部分的期权价格都集中在平均值附近。

• 期权价格的分布的最大值和最小值分别是0.63和0.58，这表示期权价格的范围是有限的，不会出现极端的情况。

示例2-用蒙特卡罗方法估计一个函数的积分的值，并用图形展示误差的分布

示例所使用的原理是蒙特卡罗方法，它是一种通过随机抽样来估计积分的数值方法。蒙特卡罗方法的基本思想是，将积分转换为期望的形式，然后用样本均值来近似总体期望，从而得到积分的近似值。

# 用蒙特卡罗方法估计一个函数的积分的值，并用图形展示误差的分布
# 导入随机数、数值计算、绘图、数学、统计的模块
import random
from matplotlib.pyplot import sci 
import numpy as np 
import matplotlib.pyplot as plt 
import math 
from scipy import stats as stats
import statistics 


# 定义积分的上下限
a = -np.pi/2
b =  np.pi/2
exactValue = 0 # 精确的积分值，这里为0
NumAttempts = 5000  # 模拟的次数
# 定义被积函数，这里是余弦函数
goldenValue = 2.0 # 函数在积分区间的平均值，这里为2
def f(x): 
    return np.cos(x) 


# 创建几个空列表，用于存储模拟的结果和绘图的数据
plt_vals = [] 
plt_num_of_eval=[]
plt_std_devs = list()
plt_std_devs_accurate = list()
max_point = 1000000 # 每次模拟的最大点数


antithetic_0       = True # 是否使用对偶变量的方法，这里为True
antithetic_classic = False # 是否使用经典的对偶变量的方法，这里为False
target_error = float(5) #% # 目标的误差百分比，这里为5%
rng = np.random.default_rng(12345) # 创建一个随机数生成器，指定种子为12345
for i in range(1, NumAttempts): # 循环NumAttempts次，进行模拟         
    if (i % 1000==0) : # 每隔1000次，打印当前的轨迹数
        print ("Trajectory: ", i)     
    mean   = 0.0 # 初始化平均值为0
    sum_sq = 0 # 初始化平方和为0
    sumOfFunc = 0 # 初始化函数值之和为0
    sum_sq_anthi = 0 # 初始化对偶变量的平方和为0
    
    fvals = list() # 创建一个空列表，用于存储函数值
    I = (b-a) # 计算积分区间的长度
    xprev = 0 # 初始化上一个随机点的横坐标为0
    for pointIdx in range(1,max_point): # 循环max_point次，生成随机点
        #x = random.uniform(a,b)  # 用均匀分布生成一个随机数，作为横坐标
        x = rng.uniform(a,b) # 用随机数生成器生成一个随机数，作为横坐标
        if antithetic_0 and pointIdx%2 == 0: # 如果使用对偶变量的方法，并且是偶数个点
            x = b - xprev + a # 用对称的方法生成另一个横坐标
            
        fx = I*f(x) # 计算函数值，乘以积分区间的长度，得到积分的估计值
                
        if (i % 10000 == 0) : # 每隔10000次，打印当前的点数
            print ("\tPoint: ", i) 
            
        if antithetic_classic: # 如果使用经典的对偶变量的方法
            x1 = b - xprev + a # 用对称的方法生成另一个横坐标
            fx = fx + I*f(x1) # 计算另一个函数值，乘以积分区间的长度，加到之前的估计值上
            fx = fx/2 # 取平均值，得到积分的估计值
            
        sumOfFunc += fx # 将积分的估计值累加到函数值之和中
        
        sum_sq   += fx*fx # 将积分的估计值的平方累加到平方和中    
        
        fxprev = fx # 记录当前的积分的估计值
        xprev = x # 记录当前的横坐标


        #fvals.append(fx) # 将积分的估计值添加到函数值的列表中
        if (pointIdx > 10 and pointIdx % 1==0): # 如果点数大于10，并且是整数倍
            mean =  sumOfFunc/pointIdx # 计算函数值之和除以点数，得到平均值   
            variance_2 = (sum_sq /float(pointIdx) - mean*mean) /float(pointIdx-1) # 计算方差的无偏估计，等于平方和除以点数减去平均值的平方，再除以点数减一        
            
            eps = 1e-8; # 定义一个很小的数，用于避免负数的出现
            if (variance_2 < -eps) : # 如果方差的估计值小于负的eps
                variance_2 = 0 # 将方差的估计值设为0
            
            std_dev = math.sqrt(variance_2) # 计算标准差，等于方差的平方根
            error = 100 * std_dev / abs(mean) # 计算误差的百分比，等于标准差除以平均值的绝对值，再乘以100
            if(error < target_error): # 如果误差的百分比小于目标的误差百分比
                break # 跳出循环，结束模拟


    std_dev_accurate = 0 # 初始化精确的标准差为0
    for ff in fvals: # 循环遍历函数值的列表
        std_dev_accurate += (ff-mean)*(ff-mean) # 计算函数值减去平均值的平方，累加到精确的标准差中
    std_dev_accurate = 100 * std_dev_accurate/float(pointIdx-1) # 将精确的标准差除以点数减一，再乘以100，得到精确的误差的百分比
    std_dev_accurate = std_dev_accurate  / abs(mean) #relative # 将精确的误差的百分比除以平均值的绝对值，得到相对的误差的百分比
    
    plt_std_devs_accurate.append(std_dev_accurate) # 将精确的误差的百分比添加到列表中
    
    ans = sumOfFunc/float(pointIdx) # 计算函数值之和除以点数，得到积分的估计值  
    plt_vals.append(ans) # 将积分的估计值添加到列表中
    plt_num_of_eval.append(pointIdx) # 将点数添加到列表中
    plt_std_devs.append(error) # 将误差的百分比添加到列表中




std_dev = math.sqrt(np.var(plt_vals)) # 计算积分的估计值的列表的标准差
post_sigma = std_dev/goldenValue*100 # 计算后验的误差的百分比，等于标准差除以函数的平均值，再乘以100
print (" Golden function value: ", goldenValue, " average ", np.average(plt_vals), " std dev ", std_dev, " sigma ", post_sigma, "%", " vs target ", post_sigma/target_error) # 打印函数的平均值，积分的估计值的平均值，标准差，后验的误差的百分比，和目标的误差的百分比的比值
print ("Average number of point to converge: ", np.average(plt_num_of_eval)) # 打印达到目标误差所需的平均点数
#print 
print (stats.normaltest(plt_vals)) # 打印积分的估计值的列表的正态性检验的结果


# 计算实际的误差的百分比，等于积分的估计值减去函数的平均值，再除以函数的平均值，再乘以100，得到一个列表
real_error          = [100*(x - goldenValue)/goldenValue for x in plt_vals]


# 设置图形的标题，显示后验的误差的百分比和目标的误差的百分比
plt.title("Postfactum errors of integral in %, target is " + str(target_error)) 
# 用黑色的边框绘制实际的误差的百分比的直方图，设置为密度图
plt.hist (real_error, bins=100, ec="black", density=True)  
# 生成一个从-5倍目标误差到5倍目标误差的等差数列，作为x轴的数据
x = np.arange(-5*target_error, 5 *target_error, 0.1)
# 用绿色的线绘制一个以0为均值，目标误差为标准差的正态分布的概率密度函数
plt.plot(x, stats.norm.pdf(x, 0, target_error), color='green')
# 用红色的线绘制一个以0为均值，后验误差为标准差的正态分布的概率密度函数
plt.plot(x, stats.norm.pdf(x, 0, post_sigma), color='red')
# 显示图形
plt.show() # shows the plot


# 暂停50秒
plt.pause(50)
# 终端输出：
Trajectory:  1000
Trajectory:  2000
Trajectory:  3000
Trajectory:  4000
 Golden function value:  2.0  average  2.0761046795629037  std dev  0.23237394311726303  sigma  11.61869715586315 %  vs target  2.3237394311726303
Average number of point to converge:  84.23104620924185
NormaltestResult(statistic=1193.3890480427926, pvalue=7.225382379205633e-260)

输出结果：

• 蒙特卡罗算法是一种通过随机抽样来估计积分的数值方法，它的误差是由样本的数量和分布决定的，通常随着样本数量的增加而减小。

• 后验误差是指在进行模拟后，根据样本的方差和均值来估计误差的大小，它是一个不确定的量，只能给出一个置信区间。

• 目标误差是指在进行模拟前，设定的期望达到的误差的百分比，它是一个确定的量，可以作为模拟的终止条件。

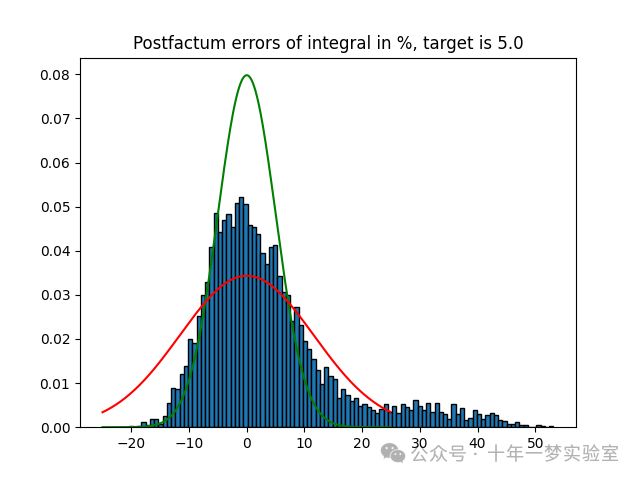
• 图像的标题显示，目标误差是5%，也就是说，希望积分的估计值与函数的平均值的差距不超过5%。

• 图像的x轴显示，实际的误差的百分比的范围是从-20%到50%，也就是说，有些积分的估计值比函数的平均值偏大，有些比函数的平均值偏小，有些接近函数的平均值。

• 图像的y轴显示，实际的误差的百分比的频率是从0到0.08，也就是说，有些误差的百分比出现的次数多，有些出现的次数少。

• 图像的蓝色条形图显示，实际的误差的百分比呈现一个近似正态分布的形状，也就是说，大部分的误差的百分比都集中在0附近，少部分的误差的百分比偏离0较远。

• 图像的绿色曲线显示，一个以0为均值，目标误差为标准差的正态分布的概率密度函数，也就是说，如果模拟的结果完全符合目标误差，那么误差的分布应该是这个曲线的形状。

• 图像的红色曲线显示，一个以0为均值，后验误差为标准差的正态分布的概率密度函数，也就是说，根据模拟的结果，可以拟合出一个最接近实际误差分布的曲线，它的标准差反映了后验误差的大小。

• 从图像中可以看出，实际的误差的分布与理论的误差的分布有一定的差异，主要是因为模拟的次数和点数不够多，导致样本的方差和均值不稳定，从而影响了误差的估计。如果增加模拟的次数和点数，那么实际的误差的分布会更接近理论的误差的分布，后验误差也会更接近目标误差。

The End