浅析Treap——平衡树
Treap,一种数据结构,支持插入节点、删除节点、求第x大的节点、求权值为x的节点的排名、求权值比x小的最大节点、求权值比x大的最小节点
提示:以下图片均由Powerpoint出品,请原谅丑陋无比的图
【引子:二叉排序树和堆】
首先,我们要知道,Treap=Tree+Heap,Tree指的是二叉排序树,Heap则是指堆
1.Tree——二叉排序树
二叉排序树,是指根的左儿子比根小,右儿子比根大,且左右子树均为二叉排序树的树
通俗来说,就是左子树全部比根小,右子树全部比根大,如图:

这时候,我们要插入一个节点,就不断地判断与根的大小关系(假设没有节点相同):
1.比根小,去左子树
2.比根大,去右子树
直到来到一个空树,插入:

删除节点:
如果一个节点是叶子节点,直接销毁
否则,如果这个节点有一个子节点,直接将其连接到该节点的父亲
否则,沿着右子树的根一路向左到底,然后用那个值替换掉要删除的节点,例如我们要删7:

因为这个点必定小于右子树的其他值,且大于左子树的全部数,所以他是作为根的最好人选
接下来,交换8和7,然后销毁7:

查询x的排名:
这个很简单,查看x与根的大小关系,如果相等,排名为左子树元素个数+1
比根小,递归查询他在左子树的排名,排名为他在左子树的排名,空树排名为0
比根大,递归查询他在右子树的排名,排名为右子树的排名+左子树元素个数+1
查询排名为x的数:
这个也很好理解,判断左子树元素个数是否大于等于之
如果是就在左子树找
否则,如果刚好为左子树元素个数+1,就是根
如果大于左子树元素个数+1,则必定在右子树,这个和查询x排名对照起来就很好理解
查询x的前驱(求权值比x小的最大节点):
空节点返回-inf
如果根的权值小于等于x,就在左子树找
否则,取根和右子树查询结果的最大值(我们要求最大节点)
查询x的后继(求权值比x大的最小节点):
空节点返回inf
如果根的权值大于等于x,就去右子树
否则,取根和左子树查询结果的最小值(我们要求最小节点)
我才不会告诉你这两段我是Ctrl C+V的
其实上面的前驱后继对照看就很好记
这时候细心的人会发现,这六个操作不就是刚刚上面讲的Treap支持的操作吗?
好吧,那如果是这样我们还写个Treap干什么?
原因看下图
恐怕是药丸了,虽然一般情况下二叉排序树复杂度不错,是 O ( l o g n ) O(logn) O(logn)
但是,不排除有丧心病狂的出题人故意卡你的情况,这时候复杂度为 O ( n ) O(n) O(n)
要怎么办呢?
堆!你值得拥有
2.Heap——堆
堆,一种完全二叉树(看看看,刚好防止了退化),保证根节点比左右子树都要大或小,大的称为大根堆,反之称小根堆。
注意,完全二叉树用数组存,i的儿子为2i和2i+1,父亲为i/2
这次先把模板呈上:
struct max_heap
{
int size;
int d[maxn];
void clear()
{
size=0;
memset(d,0,sizeof(d));
}
void push(int x)
{
d[++size]=x;
int flag=1,p=size;
while (flag && (p>1))
{
if (d[p/2]<d[p])
swap(d[p/2],d[p]);
else flag=0;
p/=2;
}
}
void pop()
{
swap(d[1],d[size]);
size--;
int p=1,t,flag=1;
while (flag && (p*2<=size))
{
if (d[p*2]>d[p]) t=p*2;
else t=p;
if (p*2<size)
if ((d[p*2+1]>d[p]) && (d[p*2+1]>d[p*2]))
t=p*2+1;
if (t!=p)
{
swap(d[p],d[t]);
p=t;
}
else flag=0;
}
}
int top()
{
return d[1];
}
}
此处以大根堆为例讲述
堆支持三种操作:插入,取极值,弹出极值(极值是最大或最小)
首先讲插入操作
如图所示,将新节点插入到二叉树底端:

然后不断让新节点向上跳,直到它小于它的父亲或成为根
如图:

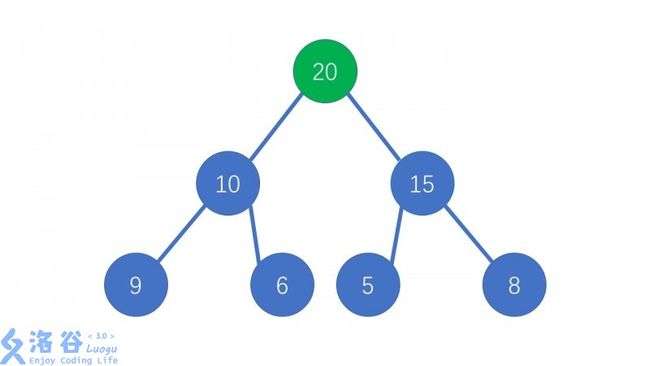
删除操作:
弹出的是极值(也就是最小或最大值)
先交换堆顶和二叉树中的最后一个元素(最后一层最右边)
然后,设p=1,判断当前p的两个儿子是否均小于p,如果是,停止循环,否则p与其中较大的那个交换,然后p赋值为较大的那个儿子的编号(说白了就是让比较牛的儿子当爹,爹去做儿子),不断循环
看图:
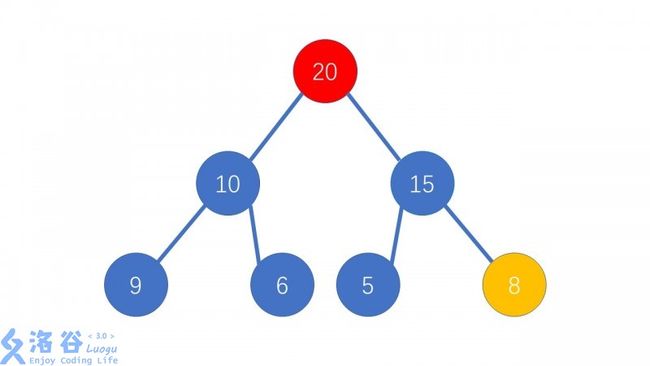


取最小或最大就是取堆顶不讲
所以呢,讲堆有什么用呢?
就是啊,有什么用呢?
和排名、前驱有什么关系啊?
别急,慢慢往下看。
【Part1:Treap的基本内容】
首先,我们需要用到以下的数组(不知道没关系,下面慢慢讲)
size[i]——以i为根的子树的节点数
v[i]——i节点的权值
num[i]——由于可能有重复(上文讲的是没有重复的),所以,我们将权值一样的存在一个节点里面,num数组存储的是i节点存的个数
son[i][2]——存储i节点的儿子,注意,这里不是完全二叉树所以需要存储儿子,son[i][0]表示左儿子,son[i][1]表示右儿子。
rd[i]——i节点的一个随机值,它有什么用呢?
堆!没错,堆正是在这里派上了用场
我们要让全部节点按照这个随机值排成一个堆
so……我们究竟要怎么解决树退化为链的问题呢?
这就引出了平衡树最重要的概念——旋转
【Part2:rotate操作——旋转】
旋转分两种,左旋和右旋,他们的共同特点是不改变Treap的二叉查找树性质,且能够使得Treap更加平衡
首先看右旋:(别问我为什么先讲右旋)
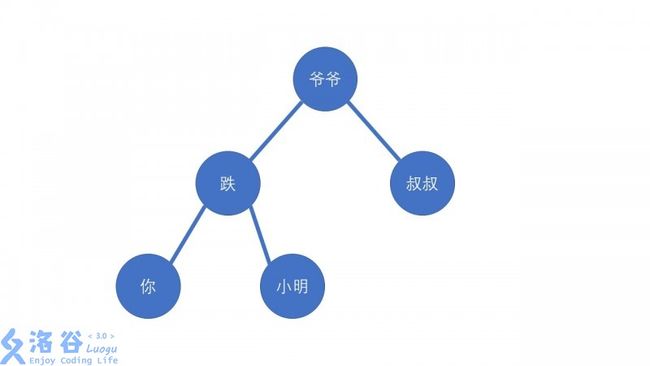
这时候,我们来进行右旋操作!

彻底乱伦了
我们来看一下大小关系:
右旋前的大小关系:你<跌<小明<爷爷<叔叔
右旋后:你<跌<小明<爷爷<叔叔
神奇吧!没有变!
然后是左旋(图偷懒了):
A
/ \
B C
/ \
D E
然后让我们来进行一次左旋
C
/ \
A E
/ \
B D
左旋之前的大小关系:B
那么,左右旋究竟是来做什么的呢?
旋转可以维护Treap堆的性质,然后巧妙地防止退化,使得操作的时间复杂度趋于 O ( l o g n ) O(logn) O(logn),从而完成任务
同时,在某些操作中需要移动节点的操作,可以直接旋转
【Part3:Treap的代码实地讲解】
模板题P3369
为了方便讲解,先挂上我巨丑无比的代码
#includepushup(p)——顾名思义,拿儿子更新父亲p的节点数
void pushup(int p)
{
size[p]=size[son[p][0]]+size[son[p][1]]+num[p];
}
p的节点数=左右儿子节点数之和+p本身存有数量
rotate(&p,d)——以p为根(可能有变)旋转,d=0左旋,d=1右旋
void rotate(int &p,int d)
{
int k=son[p][d^1];
son[p][d^1]=son[k][d];
son[k][d]=p;
pushup(p);
pushup(k);
p=k;
}
让我们以d=0时左旋为例:
A(p)
/ \
B C(k)
/ \
D E
k=p的右儿子(暂时保存)
p的右儿子变成k的左儿子
A(p)
/ \
B D C(k)
\
E
k的左儿子变成p
C(k)
/ \
(p)A E
/ \
B D
然后先pushup子代p的,再pushup父代k的
最后换根即可
C(p)
/ \
A E
/ \
B D
ins(&p,x)——根为p,插入节点x(因为需要rotate所以要传引用)
void ins(int &p,int x)
{
if (!p)
{
p=++sum;
size[p]=num[p]=1;
v[p]=x;
rd[p]=rand();
return;
}
if (v[p]==x)
{
num[p]++;
size[p]++;
return;
}
int d=(x>v[p]);
ins(son[p][d],x);
if (rd[p]<rd[son[p][d]]) rotate(p,d^1);
pushup(p);
}
首先是第一种情况——!p,也就是说当前是一个空节点
那么节点总数++,然后开辟一个新节点
size[p]=1,共有1个节点在树中
v[p]=x,值为x
num[p]=1,当前节点有一个重复数字
rd[p]=rand(),生成随机值,拿来维护堆
情况2,有一个数和要插入的x重复,那么直接个数加加即可
否则,我们需要找一个子树,使得Treap的二叉排序树性质成立 一个一个情况来看: 1.空节点,直接返回掉 1.空节点不解释 1.空节点,没有前驱 与前驱超级类似 1.线段树套平衡树,求区间前驱后继排名(就是线段树的每个节点都是一个平衡树) 我也不知道这是哪个神仙想出来的,Treap十分的优美,实现简单(上面的代码,每个函数四五行),而且功能强大,思想巧妙。
以x>v[p]的情况为例
d=1,此时去p的右子树。
如果加完以后p的随机值小于它的右儿子,直接左旋调整(重点,想一想,为什么这样转不破坏堆的性质)
xdel(&p,x)——根为p,删掉节点xvoid del(int &p,int x)
{
if (!p) return;
if (x<v[p]) del(son[p][0],x);
else if (x>v[p]) del(son[p][1],x);
else
{
if (!son[p][0] && !son[p][1])
{
num[p]--; size[p]--;
if (num[p]==0) p=0;
}
else if (son[p][0] && !son[p][1])
{
rotate(p,1);
del(son[p][1],x);
}
else if (!son[p][0] && son[p][1])
{
rotate(p,0);
del(son[p][0],x);
}
else if (son[p][0] && son[p][1])
{
int d=(rd[son[p][0]]>rd[son[p][1]]);
rotate(p,d);
del(son[p][d],x);
}
}
pushup(p);
}
1.空节点,根本就没这个数,直接返回
2.如果x和v[p]不相等,直接去相应子树解决问题
3.如果x=v[p]
3a.x是叶子节点,直接扣掉个数,如果个数为零删掉节点
3b.有一个子节点,直接把子节点旋转上来,然后去相应子树解决
3c.两个子节点,把大的那个转上来,然后去另一个子树解决rank(p,x)——根为p,查x在根为p的树中的排名int rank(int p,int x)
{
if (!p) return 0;
if (v[p]==x) return size[son[p][0]]+1;
if (v[p]<x) return size[son[p][0]]+num[p]+rank(son[p][1],x);
if (v[p]>x) return rank(son[p][0],x);
}
2.x==v[p],那么左子树的全部数必定小于x,直接返回左子树节点数+1
3.x>v[p],意味着x位于右子树,那么根和左子树一定比x小,先加上,然后再加上x在右子树里面的排名即可
4.xfind(p,x)——根为p,查在根为p的子树中排名为x的数int find(int p,int x)
{
if (!p) return 0;
if (size[son[p][0]]>=x) return find(son[p][0],x);
else if (size[son[p][0]]+num[p]<x)
return find(son[p][1],x-num[p]-size[son[p][0]]);
else return v[p];
}
2.左子树节点数大于x,解在左子树中
3.左子树加根的节点数比x小,解在右子树中,查右子树的第x-<左子树节点个数>-<根储存个数>名即可
4.左子树加根的节点大于等于x,意味着要找的就是当前的根节点v[p]pre(p,x)——根为p,查在根为p的子树中x的前驱int pre(int p,int x)
{
if (!p) return -inf;
if (v[p]>=x) return pre(son[p][0],x);
else return max(v[p],pre(son[p][1],x));
}
2.如果x是根或在右子树,去左子树找
3.否则要么是根要么右子树,取一个max就可以了(前驱定义为小于x,且最大的数)suc(p,x)——根为p,查在根为p的子树中x的后继int suc(int p,int x)
{
if (!p) return inf;
if (v[p]<=x) return suc(son[p][1],x);
else return min(v[p],suc(son[p][0],x));
}
1.空节点无后继
2.如果在根或者左子树,去右子树找
3.否则要么根要么左子树,取min就可以了(后继定义为大于x,且最小的数)【Part4:Treap的拓展应用】
2.伸展树,翻转区间分割等(我才不会告诉你我也不会)【Part5:结语】
这给我们很大的启发,Treap正是成功地结合了二叉排序树与堆的优点,秒杀众多数据结构,如果一个人能够结合两者或更多的优点加以运用,那么这个人的人生无疑是优美而且成功的
