代码随想录 算法训练营第十五天 | 层序遍历 10道题,226.翻转二叉树, 101.对称二叉树 2
层序遍历 10道题目
题目1:102.二叉树的层序遍历(opens new window)【自上而下】
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
代码:
import collections
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root]) # 创建一个双端队列,把根节点加入其中
result = [] # 储存结果的数组
while queue: # 当队列不为空
level = [] # 创建一个空列表,存储每一层的遍历结果
for _ in range(len(queue)): # 遍历每一层,遍历次数为每一层队列的长度
cur = queue.popleft() # 取出队列左侧的结点cur,
level.append(cur.val) # 添加到当前层的结果中
# 到这里,一层的遍历结束,下面是为下一层遍历做准备
if cur.left: # 如果当前结点的左子节点存在,添加到队列中
queue.append(cur.left)
if cur.right: # 右子节点存在的话,添加到队列中
queue.append(cur.right)
result.append(level)
return result
题目2:107二叉树的层次遍历II【自下而上】
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
代码:
和自上而下一样的,只是最后打印结果的时候倒序打印即可。
return result[::-1]
题3:199.二叉树的右视图
题目
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
代码 :
import collections
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root:
return []
queue = collections.deque([root])
right_view = [] # 创建一个数组存储右边的视图
while queue: # 只要队列不为空
level_size = len(queue)
for i in range(level_size):
node = queue.popleft() # 移除并返回队列的第一个数
if i == level_size - 1: # 当i是队列中的最后一个元素
right_view.append(node.val) # 把最后这个元素结点的值添加道右视图的数组中
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return right_view题4:637.二叉树的层平均值
题目:
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
输入:root = [3,9,20,null,null,15,7]
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
代码:
import collections
class Solution:
def averageOfLevels(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root]) # 创建一个双端队列,把根节点加入其中
result = [] # 储存结果的数组
while queue: # 当队列不为空
level = [] # 创建一个空列表,存储每一层的遍历结果
for _ in range(len(queue)): # 遍历每一层,遍历次数为每一层队列的长度
cur = queue.popleft() # 取出队列左侧的结点cur,
level.append(cur.val) # 添加到当前层的结果中
# 到这里,一层的遍历结束,下面是为下一层遍历做准备
if cur.left: # 如果当前结点的左子节点存在,添加到队列中
queue.append(cur.left)
if cur.right: # 右子节点存在的话,添加到队列中
queue.append(cur.right)
# 在题目1的基础上做下面3行操作即可
n=len(level)
m=sum(level)
average=m/n
result.append(average)
return result题5:429.N叉树的层序遍历
题目:
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
代码:
import collections
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root]) # 创建一个双端队列,把根节点加入其中
result = [] # 储存结果的数组
while queue: # 当队列不为空
level = [] # 创建一个空列表,存储每一层的遍历结果
for _ in range(len(queue)): # 遍历每一层,遍历次数为每一层队列的长度
cur = queue.popleft() # 取出队列左侧的结点cur,
level.append(cur.val) # 添加到当前层的结果中
# 这一步是本题和其他题目不同之处,主要是处理结点的子孩子
for child in cur.children:
queue.append(child)
result.append(level)
return result题6:515.在每个树行中找最大值
题目:
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
代码:
import collections
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root]) # 创建一个双端队列,把根节点加入其中
result = [] # 储存结果的数组
while queue: # 当队列不为空
# 这是本题的不同之处
max_val = float('-inf') # 定义一个最大值,数值为负无穷大,这样可以使得每一层的每一个数都能进行比较
for _ in range(len(queue)): # 遍历每一层,遍历次数为每一层队列的长度
cur = queue.popleft() # 取出队列左侧的结点cur,
max_val = max(max_val, cur.val) # 让一层中的每个结点都和最大值比较
# 让每一个结点的左右结点进入队列
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(max_val)
return result
题7.116填充每个节点的下一个右侧节点指针
题目:
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
代码:
"""
# Definition for a Node.
class Node:
def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
self.val = val
self.left = left
self.right = right
self.next = next
"""
import collections
# 题目的意思是:每个结点的右边如果有相邻的结点,则把指针指向这个结点
class Solution:
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:
return root # 这里很重要,不是返回空列表[],因为上面声明了得是结点的类型
queue = collections.deque([root]) # 创建一个双端队列,把根节点加入其中
while queue: # 当队列不为空
# 这是本题的不同之处
prev = None # 定义前一个结点,指向空
for _ in range(len(queue)): # 遍历每一层,遍历次数为每一层队列的长度
cur = queue.popleft() # 取出队列左侧的结点cur,
if prev: # 如果前一个结点存在
prev.next = cur
prev = cur # 更新前一个结点
# 让每一个结点的左右结点进入队列
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
return root # 返回根节点
题8:117 填充每个节点的下一个右侧节点指针II
题目:
和上一道题目相比,不同在于:给定一个二叉树:
代码:和上一题一样。
因为完美二叉树属于二叉树。
题9:104 二叉树的最大深度
题目:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0 # 返回0很重要,因为题目要求返回是一个整数
depth = 0 # 初始的深度为0
queue = collections.deque([root])
while queue:
depth += 1
for _ in range(len(queue)):
node = queue.popleft()
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return depth
题10.二叉树的最小深度
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import collections
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
depth = 0
queue = collections.deque([root])
while queue:
depth += 1
for _ in range(len(queue)):
node = queue.popleft()
if not node.left and not node.right: # 判断当前结点是不是叶子节点,如果没有左孩子或者右孩子,说明是叶子节点
return depth
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return depth
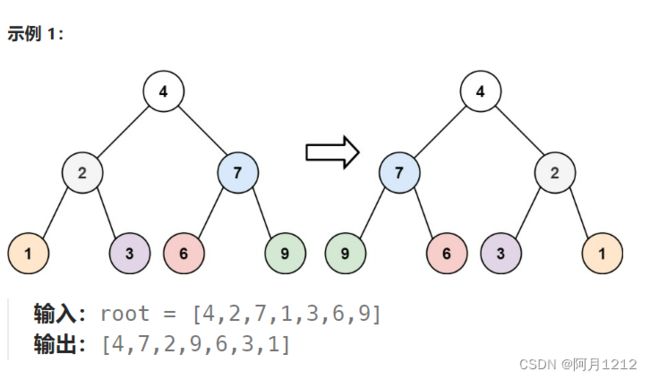
226.翻转二叉树
题目:
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
代码:
递归:前序+后序 中序不写。
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
# 1 递归——前序:
# 这里是对于根节点的处理,这一句在使用递归的前面说明是前序,在后面就是后序
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
# root.left, root.right = root.right, root.left
""" 2 递归——后序遍历
self.invertTree(root.left)
self.invertTree(root.right)
root.left, root.right = root.right, root.left
"""
return root迭代法:
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 3 迭代法——前序遍历
if not root:
return None
stack = [root] # 借助栈实现迭代
while stack:
node = stack.pop()
node.left, node.right = node.right, node.left
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return root
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 4 迭代法——后序遍历
if not root:
return None
stack = [root] # 借助栈实现迭代
while stack:
node = stack.pop()
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
node.left, node.right = node.right, node.left
return root
层序遍历:
import collections
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
queue = collections.deque([root])
while queue:
for i in range(len(queue)):
node = queue.popleft()
node.left, node.right = node.right, node.left
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return root101.对称二叉树 2
题目:
给你一个二叉树的根节点 root , 检查它是否轴对称。
代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True # 空结点是对称的
return self.compare(root.left, root.right)
def compare(self, left, right):
# 排除几种常见的情况
if left == None and right != None:
return False
elif left != None and right == None:
return False
elif left == None and right == None:
return True
elif left.val != right.val:
return False
outside = self.compare(left.left, right.right) # 外侧:左节点的左孩子,右节点的右孩子
inside = self.compare(left.right, right.left) # 内侧:左节点的有孩子,右节点的左孩子
isSame = outside and inside # 逻辑运算得到isSame,所以它是一个布尔型的值
return isSame
总结:
一共12道题目,花了2天时间看完。
昨晚整个人已经有些混乱了,一刷属于看得懂,但是写完之后不知道自己留下些什么,生怕下次再见完全不懂。写博客也是为了方便自己回顾。
以前比较害怕递归,但是这两天看了递归、迭代、层序遍历,感觉都还行,属于一个难度。我对于这三者的记忆主要是如下特点:
递归:记住三部曲,定义的函数会在后面调用
迭代:借助栈
层序遍历:借助队列