Hash的应用
学习资料:论文一,论文二
Rabin-Karp string search algorithm
1.pku-1200
描述:求在文本中出现的不同子串(给定长度)的个数。
分析:最初"You may assume that the maximum number of substrings formed by the possible set of characters does not exceed 16 Millions."
这句理解有误,正确的理解是:nc^n <= 16,000,000,根据这个条件可以确定用nc进制hash(R-K algorithm),并且不需要处理冲突。
 代码
代码
#include
<
stdio.h
>
#include
<
string
.h
>
#define
NL 20000000
char
s[NL];
int
n, nc;
int
b[
30
];
int
v[
255
];
bool
hash[NL];
int
main() {
while
(scanf(
"
%d%d
"
,
&
n,
&
nc)
!=
EOF) {
scanf(
"
%s
"
, s);
b[
0
]
=
1
;
for
(
int
i
=
1
; i
<
n; i
++
) {
b[i]
=
b[i
-
1
]
*
nc;
}
int
len
=
strlen(s);
if
(len
<
n) {
printf(
"
0\n
"
);
continue
;
}
memset(v,
-
1
,
sizeof
(v));
//
提取出字符集,对应到0~nc-1
for
(
int
i
=
0
, j
=
0
; i
<
len; i
++
) {
if
(v[s[i]]
<
0
) {
v[s[i]]
=
j
++
;
}
}
//
R-K algorithm
memset(hash,
0
,
sizeof
(hash));
int
key
=
0
;
for
(
int
i
=
0
; i
<
n; i
++
) {
key
+=
b[i]
*
v[s[i]];
}
int
sum
=
1
;
hash[key]
=
1
;
for
(
int
i
=
1
; i
<=
len
-
n; i
++
) {
key
=
(key
-
v[s[i
-
1
]])
/
nc
+
v[s[i
+
n
-
1
]]
*
b[n
-
1
];
if
(
!
hash[key]) {
hash[key]
=
1
;
sum
++
;
}
}
printf(
"
%d\n
"
, sum);
}
return
0
;
}
//
79ms
2.pku-1635[zju-1990]
描述:判定树的同构(根结点固定),树的最小表示法。
反思:用C实现很麻烦,换成string,但效率就不是很高了,TLE一次。
 代码
代码
#include
<
stdio.h
>
#include
<
iostream
>
#include
<
string
>
#include
<
vector
>
#include
<
algorithm
>
using
namespace
std;
#define
NL 3010
void
srt(
string
s,
int
n,
string
&
cs) {
vector
<
string
>
sub;
string
ss;
int
z, o, t
=
0
, i
=
0
, k
=
0
;
z
=
o
=
0
;
while
(i
<
n) {
if
(s[i]
==
'
0
'
) z
++
;
else
o
++
;
k
++
;
/*
* 0和1的个数相同时说明已经遍历了结点的一个分支,去掉开头的0和结尾的1就是相应的子树;
* 然后递归,将所有的子树按字典序排列,得到最小表示法,最后比较是否相同。
*/
if
(z
==
o) {
if
(k
>
2
) {
srt(s.substr(t
+
1
, k
-
2
), k
-
2
, ss);
ss.insert(
0
,
"
0
"
);
ss.insert(k
-
1
,
"
1
"
);
sub.push_back(ss);
}
else
{
sub.push_back(
"
01
"
);
}
t
=
i
+
1
;
k
=
0
;
z
=
0
;
o
=
0
;
}
i
++
;
}
sort(sub.begin(), sub.end());
cs
=
""
;
vector
<
string
>
::iterator it
=
sub.begin();
while
(it
!=
sub.end()) {
cs
+=
*
it;
it
++
;
}
}
int
main() {
//
freopen("datain", "r", stdin);
int
n;
string
s1, s2, cs1, cs2;
cin
>>
n;
while
(n
--
) {
cin
>>
s1
>>
s2;
srt(s1, s1.length(), cs1);
srt(s2, s2.length(), cs2);
if
(cs1
==
cs2) {
cout
<<
"
same\n
"
;
}
else
{
cout
<<
"
different\n
"
;
}
}
return
0
;
}
//
469ms
3.poj-1971
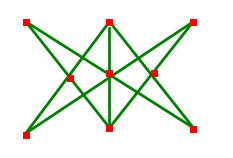
描述:平面上n个点,能构成多少个平行四边形。
思路:根据定理“平行四边形的对角线相互平分”,求出C(n,2)条线段的中点,中点重合的线段可以组合构成平行四边形。(见下图)
 代码
代码
#include
<
stdio.h
>
#include
<
stdlib.h
>
#include
<
math.h
>
#include
<
algorithm
>
#define
EP 1e-10
#define
NL 1001
using
namespace
std;
struct
Node {
int
x, y;
} p[NL];
int
dcmp(
double
x,
double
y) {
if
(fabs(x
-
y)
<
EP)
return
0
;
return
x
<
y
?
-
1
:
1
;
}
struct
L {
double
mdx, mdy;
bool
operator
<
(
const
L
&
a)
const
{
if
(dcmp(mdx, a.mdx)
==
0
) {
return
dcmp(mdy, a.mdy)
<
0
?
1
:
0
;
}
return
dcmp(mdx, a.mdx)
<
0
?
1
:
0
;
}
} l[NL
*
NL];
int
cmp(
const
void
*
a,
const
void
*
b) {
struct
L
*
x
=
(
struct
L
*
) a;
struct
L
*
y
=
(
struct
L
*
) b;
if
(dcmp(x
->
mdx, y
->
mdx)
==
0
) {
return
dcmp(x
->
mdy, y
->
mdy);
}
return
dcmp(x
->
mdx, y
->
mdx);
}
int
main() {
//
freopen("data.in", "r", stdin);
int
t, n;
scanf(
"
%d
"
,
&
t);
while
(t
--
) {
scanf(
"
%d
"
,
&
n);
for
(
int
i
=
0
; i
<
n; i
++
) {
scanf(
"
%d%d
"
,
&
p[i].x,
&
p[i].y);
}
int
m
=
0
;
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
i
+
1
; j
<
n; j
++
, m
++
) {
l[m].mdx
=
(p[i].x
+
p[j].x)
*
1.0
/
2
;
l[m].mdy
=
(p[i].y
+
p[j].y)
*
1.0
/
2
;
}
}
sort(l, l
+
m);
double
px, py;
px
=
l[
0
].mdx;
py
=
l[
0
].mdy;
int
oz
=
0
, sum
=
0
;
for
(
int
i
=
1
; i
<
m; i
++
) {
if
(fabs(px
-
l[i].mdx)
<
EP
&&
fabs(py
-
l[i].mdy)
<
EP) {
oz
++
;
}
else
{
sum
+=
(oz
+
1
)
*
oz
/
2
;
oz
=
0
;
px
=
l[i].mdx;
py
=
l[i].mdy;
}
}
sum
+=
(oz
+
1
)
*
oz
/
2
;
printf(
"
%d\n
"
, sum);
}
return
0
;
}
//
1641ms
4.poj-2002
描述:平面上n个点,能构成多少个正方形。
思路:对点hash;枚举边,计算出对应的能与其构成正方形的点,用hash判断是否存在。
知识:已知两点(x1,y1) , (x2,y2) 对应的有向线段是(x2-x1,y2-y1), 与其垂直的有向线段可以表示为,(y2-y1,x1-x2) 或 (y1-y2, x2-x1)
ps: hash函数不同时间效率会有很大不同,需要优化
 代码
代码
#include
<
stdio.h
>
#include
<
string
.h
>
#define
NL 1001
#define
MD 199997
#define
ADD 20010
int
hash[MD];
struct
POINT {
int
x, y;
}p[NL];
void
dh(
int
k) {
int
key
=
((p[k].x
+
ADD)
*
1000
+
(p[k].y
+
ADD))
%
MD;
//
int key = (p[k].x+p[k].y+MD+MD)%MD;
while
(hash[key]
>=
0
) {
key
=
(key
+
1
)
%
MD;
}
hash[key]
=
k;
}
int
dh1(POINT po) {
int
key
=
((po.x
+
ADD)
*
1000
+
(po.y
+
ADD))
%
MD;
//
int key = (po.x+po.y+MD+MD)%MD;
while
(hash[key]
>=
0
) {
int
t
=
hash[key];
if
(p[t].x
==
po.x
&&
p[t].y
==
po.y) {
return
1
;
}
key
=
(key
+
1
)
%
MD;
}
return
0
;
}
int
main()
{
//
freopen("data.in", "r", stdin);
int
n;
while
(scanf(
"
%d
"
,
&
n)
!=
EOF) {
if
(
!
n)
break
;
memset(hash,
-
1
,
sizeof
(hash));
for
(
int
i
=
0
; i
<
n; i
++
) {
scanf(
"
%d%d
"
,
&
p[i].x,
&
p[i].y);
dh(i);
}
int
sum
=
0
;
POINT p1, p2, dr1, dr2;
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
i
+
1
; j
<
n; j
++
) {
dr1.x
=
p[i].y
-
p[j].y;
dr1.y
=
p[j].x
-
p[i].x;
dr2.x
=
p[j].y
-
p[i].y;
dr2.y
=
p[i].x
-
p[j].x;
p1.x
=
p[i].x
+
dr1.x;
p1.y
=
p[i].y
+
dr1.y;
p2.x
=
p[j].x
+
dr1.x;
p2.y
=
p[j].y
+
dr1.y;
int
ok1, ok2;
ok1
=
dh1(p1);
ok2
=
dh1(p2);
if
(ok1
&
ok2) {
sum
++
;
}
p1.x
=
p[i].x
+
dr2.x;
p1.y
=
p[i].y
+
dr2.y;
p2.x
=
p[j].x
+
dr2.x;
p2.y
=
p[j].y
+
dr2.y;
ok1
=
dh1(p1);
ok2
=
dh1(p2);
if
(ok1
&
ok2) {
sum
++
;
}
}
}
printf(
"
%d\n
"
, sum
/
4
);
}
return
0
;
}
//
1600+ms
