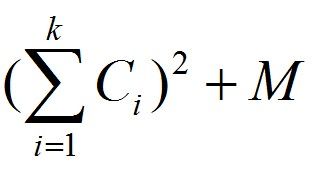- day15|前端框架学习和算法
universe_01
前端算法笔记
T22括号生成先把所有情况都画出来,然后(在满足什么情况下)把不符合条件的删除。T78子集要画树状图,把思路清晰。可以用暴力法、回溯法和DFS做这个题DFS深度搜索:每个边都走完,再回溯应用:二叉树搜索,图搜索回溯算法=DFS+剪枝T200岛屿数量(非常经典BFS宽度把树状转化成队列形式,lambda匿名函数“一次性的小函数,没有名字”setup语法糖:让代码更简洁好写的语法ref创建:基本类型的
- C++ 计数排序、归并排序、快速排序
每天搬一点点砖
c++数据结构算法
计数排序:是一种基于哈希的排序算法。他的基本思想是通过统计每个元素的出现次数,然后根据统计结果将元素依次放入排序后的序列中。这种排序算法适用于范围较小的情况,例如整数范围在0到k之间计数排序步骤:1初始化一个长度为最大元素值加1的计数数组,所有元素初始化为02遍历原始数组,将每个元素值作为索引,在计数数组中对应位置加13将数组清空4遍历计数器数组,按照数组中的元素个数放回到元数组中计数排序的优点和
- 【C++算法】76.优先级队列_前 K 个高频单词
流星白龙
优选算法C++c++算法开发语言
文章目录题目链接:题目描述:解法C++算法代码:题目链接:692.前K个高频单词题目描述:解法利用堆来解决TopK问题预处理一下原始的字符串数组,用一个哈希表统计一下每一个单词出现的频次。创建一个大小为k的堆频次:小根堆字典序(频次相同的时候):大根堆循环让元素依次进堆判断提取结果C++算法代码:classSolution{//定义类型别名,PSI表示对typedefpairPSI;//自定义比较
- 关于流媒体播放器EasyPlayer和EasyPlayerPro的介绍以及其区别
EasyDarwin
EasyDarwin音视频ffmpeg人工智能大数据ar
EasyPlayer是一款流媒体播放器系列项目,它支持多种流媒体协议的播放,包括但不限于RTSP、RTMP、HTTP、HLS、UDP、RTP、File等。除此之外,EasyPlayer还支持本地文件播放和多种功能特性,包括本地抓拍、本地录像、播放旋转、多屏播放、倍数播放等。EasyPlayer核心基于ffmpeg,稳定、高效、可靠、可控。随着多年的不断发展和迭代,EasyPlayer基于成功的实践
- 力扣面试题07 - 旋转矩阵
茶猫_
leetcode矩阵算法c语言
题目:给你一幅由N×N矩阵表示的图像,其中每个像素的大小为4字节。请你设计一种算法,将图像旋转90度。不占用额外内存空间能否做到?示例1:给定matrix=[[1,2,3],[4,5,6],[7,8,9]],原地旋转输入矩阵,使其变为:[[7,4,1],[8,5,2],[9,6,3]]示例2:给定matrix=[[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,
- 模拟退火(SA):如何“故意走错路”,才能找到最优解?
小瑞瑞acd
小瑞瑞学数模模拟退火算法python启发式算法算法
模拟退火(SA):如何“故意走错路”,才能找到最优解?图示模拟退火算法如何通过接受较差解(橙色虚线标注)从局部最优(绿色点)逃逸,最终找到全局最优解(紫色点),展示其跳出局部极小值的能力。大家好,我是小瑞瑞!欢迎回到我的专栏!想象一下,你站在一座连绵不绝的山脉中,目标是找到海拔最低的那个山谷。你手上只有一个高度计,视野被浓雾笼罩,只能看清脚下的一小片区域。如果你是一个“贪心”的登山者,你的策略会非
- 编程算法:技术创新的引擎与业务增长的核心驱动力
在数字经济时代,算法已成为推动技术创新与业务增长的隐形引擎。从存内计算突破冯·诺依曼瓶颈,到动态规划优化万亿级金融交易,编程算法正在重塑产业竞争格局。一、存内计算:突破冯·诺依曼瓶颈的算法革命1.1存内计算的基本原理传统计算架构中90%的能耗消耗在数据搬运上。存内计算(Processing-in-Memory)通过直接在存储单元执行计算,实现能效10-100倍提升:#传统计算vs存内计算能耗模型i
- 图论算法经典题目解析:DFS、BFS与拓扑排序实战
周童學
数据结构与算法深度优先算法图论
图论算法经典题目解析:DFS、BFS与拓扑排序实战图论问题是算法面试中的高频考点,本博客将通过四道LeetCode经典题目(均来自"Top100Liked"题库),深入讲解图论的核心算法思想和实现技巧。涵盖DFS、BFS、拓扑排序和前缀树等知识点,每道题配有Java实现和易错点分析。1.岛屿数量(DFS遍历)问题描述给定一个由'1'(陆地)和'0'(水)组成的二维网格,计算岛屿的数量。岛屿由水平或
- 5G-RAN与语义通信RAN
一去不复返的通信er
智简网络&语义通信5G人工智能语义通信
1️⃣RAN协议栈与TCP/IP五层协议栈的对应关系a.物理层(TCP/IP)↔PHY(RAN)对应关系:5GNRRAN的物理层直接对应TCP/IP的物理层。功能对比:TCP/IP物理层:负责比特流的物理传输,如通过电缆、光纤或无线介质传输信号。RAN物理层:处理无线信号的调制、编码、信道估计和传输(如OFDM、LDPC编码)。在5GNR中,物理层负责将数据映射到无线信道(如PDSCH、PUSCH
- 代码随想录算法训练营第三十五天
01背包问题二维题目链接01背包问题二维题解importjava.util.Scanner;publicclassMain{publicstaticvoidmain(String[]args){Scannersc=newScanner(System.in);intM=sc.nextInt();intN=sc.nextInt();int[]space=newint[M];int[]value=new
- DPDK 技术详解:榨干网络性能的“瑞士军刀”
你是否曾感觉,即使拥有顶级的服务器和万兆网卡,你的网络应用也总是“喂不饱”硬件,性能总差那么一口气?传统的网络处理方式,就像在高速公路上设置了太多的收费站和检查点,限制了数据包的“奔跑”速度。今天,我们要深入探讨一个能够打破这些瓶颈,让你的网络应用快到飞起的“黑科技”——DPDK(DataPlaneDevelopmentKit,数据平面开发套件)。这不仅仅是一个工具包,更是一种全新的网络处理哲学。
- Pktgen-DPDK:开源网络测试工具的深度解析与应用
艾古力斯
本文还有配套的精品资源,点击获取简介:Pktgen-DPDK是基于DPDK的高性能流量生成工具,适用于网络性能测试、硬件验证及协议栈开发。它支持多种网络协议,能够模拟高吞吐量的数据包发送。本项目通过利用DPDK的高速数据包处理能力,允许用户自定义数据包内容,并实现高效的数据包管理与传输。文章将指导如何安装DPDK、编译Pktgen、配置工具以及使用方法,最终帮助开发者和网络管理员深入理解并优化网络
- 机器学习必备数学与编程指南:从入门到精通
a小胡哦
机器学习基础机器学习人工智能
一、机器学习核心数学基础1.线性代数(神经网络的基础)必须掌握:矩阵运算(乘法、转置、逆)向量空间与线性变换特征值分解与奇异值分解(SVD)为什么重要:神经网络本质就是矩阵运算学习技巧:用NumPy实际操作矩阵运算2.概率与统计(模型评估的关键)核心概念:条件概率与贝叶斯定理概率分布(正态、泊松、伯努利)假设检验与p值应用场景:朴素贝叶斯、A/B测试3.微积分(优化算法的基础)重点掌握:导数与偏导
- 《UNIX网络编程卷1:套接字联网API》第8章:基本UDP套接字编程深度解析
《UNIX网络编程卷1:套接字联网API》第8章:基本UDP套接字编程深度解析(8000字图文实战)一、UDP协议核心特性与编程模型1.1UDP协议设计哲学UDP(UserDatagramProtocol)是面向无连接的传输层协议(图1),其核心特征包括:无连接通信:无需三次握手,直接发送数据报尽最大努力交付:不保证可靠性、不维护连接状态报文边界保留:接收方读取的数据与发送方写入完全一致低开销高效
- 从振动信号到精准预警:AI 如何重塑工业设备健康管理?
缘华工业智维
人工智能计算机视觉边缘计算信息与通信
在智能制造浪潮席卷全球的当下,工业生产正经历着从传统模式向智能化、数字化转型的深刻变革。在这场变革中,AI驱动的振动分析技术犹如一颗璀璨新星,成为工业设备可靠运行的“健康卫士”。它通过在设备关键部位部署振动传感器,如同医生为患者听诊般实时采集设备运行时的振动信号,再借助强大的人工智能算法对这些“工业脉搏”进行深度解析,从而实现对工业设备从故障预警到寿命预测的全周期精准守护。一、AI振动分析:设备状
- 基于DeepSeek的下一代大型游戏开发革命:架构、核心技术与项目管理实践
Liudef06小白
特殊专栏人工智能AIGC架构人工智能deepseek
基于DeepSeek的下一代大型游戏开发革命:架构、核心技术与项目管理实践DeepSeek大模型正重塑游戏开发范式,本文将深入解析如何利用这一革命性技术构建下一代大型游戏,涵盖从架构设计到项目管理的全流程实践。目录DeepSeek游戏引擎核心架构1.1神经符号系统融合架构1.2动态世界生成引擎智能NPC与剧情系统2.1角色人格建模技术2.2动态叙事生成算法大型项目管理体系3.1敏捷-AI混合开发流
- 量子计算解决气候变化:科学家找到了新方法
大力出奇迹985
量子计算
气候变化已成为全球面临的严峻挑战,传统计算方法在应对与之相关的复杂问题时存在诸多局限。而量子计算作为新兴技术,为解决气候变化难题带来曙光。本文深入剖析科学家利用量子计算应对气候变化的新方法。量子计算凭借独特的量子比特与量子特性,在加速气候模型计算、优化模型参数、预测极端天气事件等方面展现出巨大优势。同时,在可再生能源整合、电网管理、碳捕获等实际应用场景中也发挥着重要作用。尽管目前面临硬件和算法等方
- 数据分析领域中AI人工智能的发展前景展望
AI大模型应用工坊
AI大模型开发实战数据分析人工智能数据挖掘ai
数据分析领域中AI人工智能的发展前景展望关键词:数据分析、人工智能、机器学习、深度学习、数据挖掘、预测分析、自动化摘要:本文深入探讨了人工智能在数据分析领域的发展现状和未来趋势。我们将从核心技术原理出发,分析AI如何改变传统数据分析范式,详细讲解机器学习算法在数据分析中的应用,并通过实际案例展示AI驱动的数据分析解决方案。文章还将探讨行业应用场景、工具生态以及未来发展面临的挑战和机遇,为数据分析师
- AI人工智能中的数据挖掘:提升智能决策能力
AI人工智能中的数据挖掘:提升智能决策能力关键词:数据挖掘、人工智能、机器学习、智能决策、数据分析、特征工程、模型优化摘要:本文深入探讨了数据挖掘在人工智能领域中的核心作用,重点分析了如何通过数据挖掘技术提升智能决策能力。文章从基础概念出发,详细介绍了数据挖掘的关键算法、数学模型和实际应用场景,并通过Python代码示例展示了数据挖掘的全流程。最后,文章展望了数据挖掘技术的未来发展趋势和面临的挑战
- 算法刷题-动态规划之背包问题
1.背包问题之01(4.30)题目描述小明有一个容量为VV的背包。这天他去商场购物,商场一共有NN件物品,第ii件物品的体积为wiwi,价值为vivi。小明想知道在购买的物品总体积不超过VV的情况下所能获得的最大价值为多少,请你帮他算算。输入描述输入第11行包含两个正整数N,VN,V,表示商场物品的数量和小明的背包容量。第2∼N+12∼N+1行包含22个正整数w,vw,v,表示物品的体积和价值。1
- 2018年中南大学中英翻译
某翁
参考:20180827235856533.jpg【1】机器学习理论表明,机器学习算法能从有限个训练集样本上得到较好的泛化【1】Machinelearningtheoryshowsthatmachinelearningalgorithmcangeneralizewellfromfinitetrainingsetsampleslimited有限的infinite无限的【2】这似乎违背了一些基本的逻辑准
- Django学习笔记(一)
学习视频为:pythondjangoweb框架开发入门全套视频教程一、安装pipinstalldjango==****检查是否安装成功django.get_version()二、django新建项目操作1、新建一个项目django-adminstartprojectproject_name2、新建APPcdproject_namedjango-adminstartappApp注:一个project
- GDP经济社会人文民生栅格数据下载网站汇总
疯狂学习GIS
本文为“GIS数据获取整理”专栏(https://blog.csdn.net/zhebushibiaoshifu/category_10857546.html)中第八篇独立博客,因此本文全部标题均由“8”开头。本文对目前主要的GDP、社会与经济数据获取网站加以整理与介绍,若需其它GIS领域数据(如遥感影像数据、气象数据、土地土壤数据、农业数据等),大家可以点击上方专栏查看,也可以看这一篇汇总文
- 时序预测 | MATLAB实现贝叶斯优化CNN-GRU时间序列预测(股票价格预测)
Matlab机器学习之心
matlabcnngru
✅作者简介:热爱数据处理、数学建模、仿真设计、论文复现、算法创新的Matlab仿真开发者。更多Matlab代码及仿真咨询内容点击主页:Matlab科研工作室个人信条:格物致知,期刊达人。内容介绍股票价格预测一直是金融领域一个极具挑战性的课题。其内在的非线性、随机性和复杂性使得传统的预测方法难以取得令人满意的效果。近年来,深度学习技术,特别是卷积神经网络(CNN)和门控循环单元(GRU)的结合,为时
- 顺时针旋转N * N 的矩阵
忆杰
算法Python矩阵python算法
顺时针旋转题目描述数据范围实现逻辑代码实现题目描述有一个NxN整数矩阵,请编写一个算法,将矩阵顺时针旋转90度。给定一个NxN的矩阵,和矩阵的阶数N,请返回旋转后的NxN矩阵。数据范围0852789963'''#第N列逆序后变成第N行#或者是第i行变成第N-i-1列代码实现classSolution:#列转换为行defline2Row(self,mat,n):arr=[]forlineinrang
- 时序预测 | MATLAB实现BO-CNN-GRU贝叶斯优化卷积门控循环单元时间序列预测
Matlab算法改进和仿真定制工程师
matlabcnngru
✅作者简介:热爱数据处理、数学建模、算法创新的Matlab仿真开发者。更多Matlab代码及仿真咨询内容点击:Matlab科研工作室个人信条:格物致知。内容介绍时间序列预测在各个领域都具有重要的应用价值,例如金融市场预测、气象预报、交通流量预测等。准确地预测未来趋势对于决策制定至关重要。近年来,深度学习技术在时间序列预测领域取得了显著进展,其中卷积神经网络(CNN)和门控循环单元(GRU)由于其强
- 使用Python和Gradio构建实时数据可视化工具
PythonAI编程架构实战家
信息可视化python开发语言ai
使用Python和Gradio构建实时数据可视化工具关键词:Python、Gradio、数据可视化、实时数据、Web应用、交互式界面、数据科学摘要:本文将详细介绍如何使用Python和Gradio框架构建一个实时数据可视化工具。我们将从基础概念开始,逐步深入到核心算法实现,包括数据处理、可视化技术以及Gradio的交互式界面设计。通过实际项目案例,读者将学习如何创建一个功能完整、响应迅速的实时数据
- 【经典面试题】【JVM与性能调优】垃圾回收算法(标记-清除算法/复制算法/标记-整理算法/CMS/G1/ZGC)
本本本添哥
归档-Inbox1001-基础开发能力面试题目汇总jvm算法
JVM自动管理内存,当对象不再被引用时,垃圾回收器(GarbageCollector)会自动释放这些对象占用的内存。标记-清除算法(Mark-Sweep):标记垃圾再清除,会产生碎片。复制算法(Copying):将存活对象复制到新区域,适合新生代,无碎片但浪费空间。标记-整理算法(Mark-Compact):标记后将存活对象移到一端,清除另一端,适合老年代。分代收集算法(GenerationalC
- 从零到一:基于差分隐私决策树的客户购买预测系统实战开发
笙囧同学
决策树算法机器学习
作者简介:笙囧同学,中科院计算机大模型方向硕士,全栈开发爱好者联系方式:
[email protected]各大平台账号:笙囧同学座右铭:偷懒是人生进步的阶梯文章导航快速导航前言-项目背景与价值项目概览-系统架构与功能技术深度解析-核心算法原理️系统实现详解-工程实践细节性能评估与分析-实验结果分析Web系统开发-前后端开发部署与运维-DevOps实践完整复现指南-手把手教程️实践案例与故障排除-问
- CMS垃圾回收器+G1垃圾回收器+ZGC垃圾回收器详解及对比
weixin_43751710
jvmjava算法
一、CMS收集器CMS(ConcurrentMarkSweep)收集器是一种以获取最短回收停顿时间为目标的收集器,是一款针对老年代的垃圾回收器,一般和Parallel回收器(一款新生代回收器,是使用复制算法的收集器,又是并行的多线程收集器,收集时会Stoptheworld)配合使用。1.工作过程从名字(包含“MarkSweep”)上就可以看出CMS收集器是基于标记-清除算法实现的,它的运作整个过程
- jQuery 跨域访问的三种方式 No 'Access-Control-Allow-Origin' header is present on the reque
qiaolevip
每天进步一点点学习永无止境跨域众观千象
XMLHttpRequest cannot load http://v.xxx.com. No 'Access-Control-Allow-Origin' header is present on the requested resource. Origin 'http://localhost:63342' is therefore not allowed access. test.html:1
- mysql 分区查询优化
annan211
java分区优化mysql
分区查询优化
引入分区可以给查询带来一定的优势,但同时也会引入一些bug.
分区最大的优点就是优化器可以根据分区函数来过滤掉一些分区,通过分区过滤可以让查询扫描更少的数据。
所以,对于访问分区表来说,很重要的一点是要在where 条件中带入分区,让优化器过滤掉无需访问的分区。
可以通过查看explain执行计划,是否携带 partitions
- MYSQL存储过程中使用游标
chicony
Mysql存储过程
DELIMITER $$
DROP PROCEDURE IF EXISTS getUserInfo $$
CREATE PROCEDURE getUserInfo(in date_day datetime)-- -- 实例-- 存储过程名为:getUserInfo-- 参数为:date_day日期格式:2008-03-08-- BEGINdecla
- mysql 和 sqlite 区别
Array_06
sqlite
转载:
http://www.cnblogs.com/ygm900/p/3460663.html
mysql 和 sqlite 区别
SQLITE是单机数据库。功能简约,小型化,追求最大磁盘效率
MYSQL是完善的服务器数据库。功能全面,综合化,追求最大并发效率
MYSQL、Sybase、Oracle等这些都是试用于服务器数据量大功能多需要安装,例如网站访问量比较大的。而sq
- pinyin4j使用
oloz
pinyin4j
首先需要pinyin4j的jar包支持;jar包已上传至附件内
方法一:把汉字转换为拼音;例如:编程转换后则为biancheng
/**
* 将汉字转换为全拼
* @param src 你的需要转换的汉字
* @param isUPPERCASE 是否转换为大写的拼音; true:转换为大写;fal
- 微博发送私信
随意而生
微博
在前面文章中说了如和获取登陆时候所需要的cookie,现在只要拿到最后登陆所需要的cookie,然后抓包分析一下微博私信发送界面
http://weibo.com/message/history?uid=****&name=****
可以发现其发送提交的Post请求和其中的数据,
让后用程序模拟发送POST请求中的数据,带着cookie发送到私信的接入口,就可以实现发私信的功能了。
- jsp
香水浓
jsp
JSP初始化
容器载入JSP文件后,它会在为请求提供任何服务前调用jspInit()方法。如果您需要执行自定义的JSP初始化任务,复写jspInit()方法就行了
JSP执行
这一阶段描述了JSP生命周期中一切与请求相关的交互行为,直到被销毁。
当JSP网页完成初始化后
- 在 Windows 上安装 SVN Subversion 服务端
AdyZhang
SVN
在 Windows 上安装 SVN Subversion 服务端2009-09-16高宏伟哈尔滨市道里区通达街291号
最佳阅读效果请访问原地址:http://blog.donews.com/dukejoe/archive/2009/09/16/1560917.aspx
现在的Subversion已经足够稳定,而且已经进入了它的黄金时段。我们看到大量的项目都在使
- android开发中如何使用 alertDialog从listView中删除数据?
aijuans
android
我现在使用listView展示了很多的配置信息,我现在想在点击其中一条的时候填出 alertDialog,点击确认后就删除该条数据,( ArrayAdapter ,ArrayList,listView 全部删除),我知道在 下面的onItemLongClick 方法中 参数 arg2 是选中的序号,但是我不知道如何继续处理下去 1 2 3
- jdk-6u26-linux-x64.bin 安装
baalwolf
linux
1.上传安装文件(jdk-6u26-linux-x64.bin)
2.修改权限
[root@localhost ~]# ls -l /usr/local/jdk-6u26-linux-x64.bin
3.执行安装文件
[root@localhost ~]# cd /usr/local
[root@localhost local]# ./jdk-6u26-linux-x64.bin&nbs
- MongoDB经典面试题集锦
BigBird2012
mongodb
1.什么是NoSQL数据库?NoSQL和RDBMS有什么区别?在哪些情况下使用和不使用NoSQL数据库?
NoSQL是非关系型数据库,NoSQL = Not Only SQL。
关系型数据库采用的结构化的数据,NoSQL采用的是键值对的方式存储数据。
在处理非结构化/半结构化的大数据时;在水平方向上进行扩展时;随时应对动态增加的数据项时可以优先考虑使用NoSQL数据库。
在考虑数据库的成熟
- JavaScript异步编程Promise模式的6个特性
bijian1013
JavaScriptPromise
Promise是一个非常有价值的构造器,能够帮助你避免使用镶套匿名方法,而使用更具有可读性的方式组装异步代码。这里我们将介绍6个最简单的特性。
在我们开始正式介绍之前,我们想看看Javascript Promise的样子:
var p = new Promise(function(r
- [Zookeeper学习笔记之八]Zookeeper源代码分析之Zookeeper.ZKWatchManager
bit1129
zookeeper
ClientWatchManager接口
//接口的唯一方法materialize用于确定那些Watcher需要被通知
//确定Watcher需要三方面的因素1.事件状态 2.事件类型 3.znode的path
public interface ClientWatchManager {
/**
* Return a set of watchers that should
- 【Scala十五】Scala核心九:隐式转换之二
bit1129
scala
隐式转换存在的必要性,
在Java Swing中,按钮点击事件的处理,转换为Scala的的写法如下:
val button = new JButton
button.addActionListener(
new ActionListener {
def actionPerformed(event: ActionEvent) {
- Android JSON数据的解析与封装小Demo
ronin47
转自:http://www.open-open.com/lib/view/open1420529336406.html
package com.example.jsondemo;
import org.json.JSONArray;
import org.json.JSONException;
import org.json.JSONObject;
impor
- [设计]字体创意设计方法谈
brotherlamp
UIui自学ui视频ui教程ui资料
从古至今,文字在我们的生活中是必不可少的事物,我们不能想象没有文字的世界将会是怎样。在平面设计中,UI设计师在文字上所花的心思和功夫最多,因为文字能直观地表达UI设计师所的意念。在文字上的创造设计,直接反映出平面作品的主题。
如设计一幅戴尔笔记本电脑的广告海报,假设海报上没有出现“戴尔”两个文字,即使放上所有戴尔笔记本电脑的图片都不能让人们得知这些电脑是什么品牌。只要写上“戴尔笔
- 单调队列-用一个长度为k的窗在整数数列上移动,求窗里面所包含的数的最大值
bylijinnan
java算法面试题
import java.util.LinkedList;
/*
单调队列 滑动窗口
单调队列是这样的一个队列:队列里面的元素是有序的,是递增或者递减
题目:给定一个长度为N的整数数列a(i),i=0,1,...,N-1和窗长度k.
要求:f(i) = max{a(i-k+1),a(i-k+2),..., a(i)},i = 0,1,...,N-1
问题的另一种描述就
- struts2处理一个form多个submit
chiangfai
struts2
web应用中,为完成不同工作,一个jsp的form标签可能有多个submit。如下代码:
<s:form action="submit" method="post" namespace="/my">
<s:textfield name="msg" label="叙述:">
- shell查找上个月,陷阱及野路子
chenchao051
shell
date -d "-1 month" +%F
以上这段代码,假如在2012/10/31执行,结果并不会出现你预计的9月份,而是会出现八月份,原因是10月份有31天,9月份30天,所以-1 month在10月份看来要减去31天,所以直接到了8月31日这天,这不靠谱。
野路子解决:假设当天日期大于15号
- mysql导出数据中文乱码问题
daizj
mysql中文乱码导数据
解决mysql导入导出数据乱码问题方法:
1、进入mysql,通过如下命令查看数据库编码方式:
mysql> show variables like 'character_set_%';
+--------------------------+----------------------------------------+
| Variable_name&nbs
- SAE部署Smarty出现:Uncaught exception 'SmartyException' with message 'unable to write
dcj3sjt126com
PHPsmartysae
对于SAE出现的问题:Uncaught exception 'SmartyException' with message 'unable to write file...。
官方给出了详细的FAQ:http://sae.sina.com.cn/?m=faqs&catId=11#show_213
解决方案为:
01
$path
- 《教父》系列台词
dcj3sjt126com
Your love is also your weak point.
你的所爱同时也是你的弱点。
If anything in this life is certain, if history has taught us anything, it is
that you can kill anyone.
不顾家的人永远不可能成为一个真正的男人。 &
- mongodb安装与使用
dyy_gusi
mongo
一.MongoDB安装和启动,widndows和linux基本相同
1.下载数据库,
linux:mongodb-linux-x86_64-ubuntu1404-3.0.3.tgz
2.解压文件,并且放置到合适的位置
tar -vxf mongodb-linux-x86_64-ubun
- Git排除目录
geeksun
git
在Git的版本控制中,可能有些文件是不需要加入控制的,那我们在提交代码时就需要忽略这些文件,下面讲讲应该怎么给Git配置一些忽略规则。
有三种方法可以忽略掉这些文件,这三种方法都能达到目的,只不过适用情景不一样。
1. 针对单一工程排除文件
这种方式会让这个工程的所有修改者在克隆代码的同时,也能克隆到过滤规则,而不用自己再写一份,这就能保证所有修改者应用的都是同一
- Ubuntu 创建开机自启动脚本的方法
hongtoushizi
ubuntu
转载自: http://rongjih.blog.163.com/blog/static/33574461201111504843245/
Ubuntu 创建开机自启动脚本的步骤如下:
1) 将你的启动脚本复制到 /etc/init.d目录下 以下假设你的脚本文件名为 test。
2) 设置脚本文件的权限 $ sudo chmod 755
- 第八章 流量复制/AB测试/协程
jinnianshilongnian
nginxluacoroutine
流量复制
在实际开发中经常涉及到项目的升级,而该升级不能简单的上线就完事了,需要验证该升级是否兼容老的上线,因此可能需要并行运行两个项目一段时间进行数据比对和校验,待没问题后再进行上线。这其实就需要进行流量复制,把流量复制到其他服务器上,一种方式是使用如tcpcopy引流;另外我们还可以使用nginx的HttpLuaModule模块中的ngx.location.capture_multi进行并发
- 电商系统商品表设计
lkl
DROP TABLE IF EXISTS `category`; -- 类目表
/*!40101 SET @saved_cs_client = @@character_set_client */;
/*!40101 SET character_set_client = utf8 */;
CREATE TABLE `category` (
`id` int(11) NOT NUL
- 修改phpMyAdmin导入SQL文件的大小限制
pda158
sqlmysql
用phpMyAdmin导入mysql数据库时,我的10M的
数据库不能导入,提示mysql数据库最大只能导入2M。
phpMyAdmin数据库导入出错: You probably tried to upload too large file. Please refer to documentation for ways to workaround this limit.
- Tomcat性能调优方案
Sobfist
apachejvmtomcat应用服务器
一、操作系统调优
对于操作系统优化来说,是尽可能的增大可使用的内存容量、提高CPU的频率,保证文件系统的读写速率等。经过压力测试验证,在并发连接很多的情况下,CPU的处理能力越强,系统运行速度越快。。
【适用场景】 任何项目。
二、Java虚拟机调优
应该选择SUN的JVM,在满足项目需要的前提下,尽量选用版本较高的JVM,一般来说高版本产品在速度和效率上比低版本会有改进。
J
- SQLServer学习笔记
vipbooks
数据结构xml
1、create database school 创建数据库school
2、drop database school 删除数据库school
3、use school 连接到school数据库,使其成为当前数据库
4、create table class(classID int primary key identity not null)
创建一个名为class的表,其有一