支持向量机原理（Support Vector Machine）学习笔记

前言

支持向量机（SVM）是以监督学习训练出来的二元分类模型，目的是将带有未知标签的数据进行合理分类。

1. SVM算法原理

假设当前数据的类别为两类，并且是线性可分的，此时我们可以找到一个超平面，使两类数据分隔开。（下面以二维数据举例）

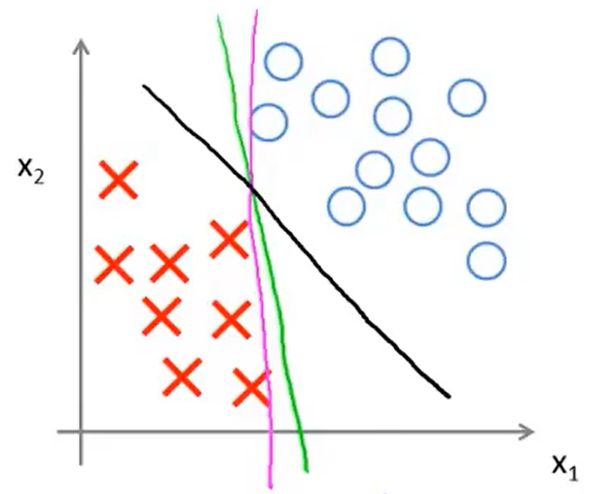
从图中可以看到，使两类数据分隔开的超平面可以有无数条，但显然粉色和绿色超平面不是那么合适，而黑色超平面则要好很多。那么如何找到像黑色超平面那样的决策边界呢？

在SVM中，我们需要找到一个超平面，使得在所有数据中离此超平面最近的数据到此超平面的间隔（margin）最大，如下图所示：

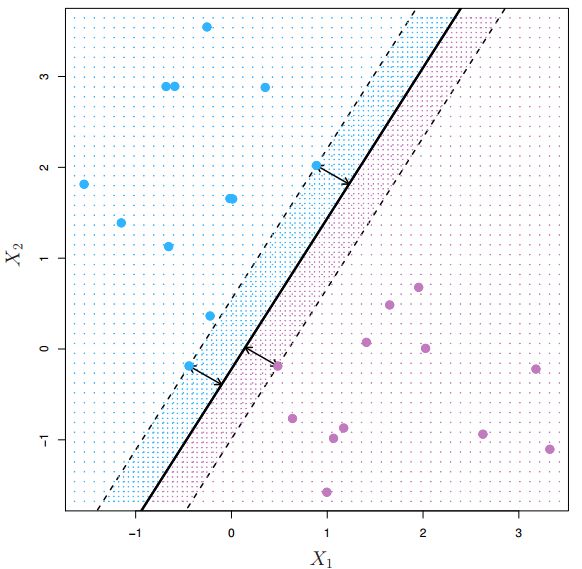
超平面只被这三个点所决定，故这些数据被称为支持向量（support vectors），虚线为间隔边界。这样决定的超平面比较健壮耐用，具有更高的容错性，因为每一边的支持向量到超平面还留有足够的距离，即使新数据出现在超平面周围（两条间隔边界内），模型对其分类的结果也有很大的可信度。

2. 硬间隔（Hard margin）SVM

硬间隔SVM模型的特点是使所有训练样本都能够被正确分类。我们假设所提供的数据都为线性可分的，也就是存在超平面使得两类的数据能够被完美地分隔开。适用硬间隔SVM模型的数据点分布如下图所示：

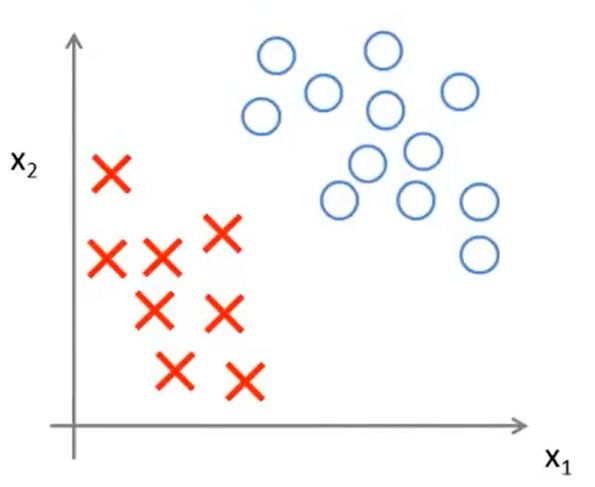
设决策边界的超平面方程为$w^{T}x+b=0$，$m$个样本$\{(x_1,y_1),(x_2,y_2),\cdots ,(x_m,y_m)\}$，$(x_i,y_i)$为第$i$个样本，$i\in 1,2,\cdots ,m$，$x_i$为第$i$个样本的特征值，以向量形式表示，$x_i\in {\mathbb{R}}^d$，$y_i$为样本的类别，$y_i\in \{-1,+1\}$。$f(x)=sign(w^{T}x+b)$为分类模型，其中$sign(x)$为指示函数：
$$sign(x)=\{\begin{array}{ll}+1,& \text{if x≥0}\\ -1,& \text{if x<0}\end{array}$$
即把输入样本的特征$x_i$代入到决策边界方程，若$w^T{x}_i+b\ge 0$，则把样本归为“+1”类，反之则归为“-1”类。

在硬间隔SVM模型中，所有训练样本需要被正确分类，因此模型需满足约束：
$$\{\begin{array}{ll}{w}^T{x}_i+b\ge 0,& \text{if yi=+1}(1)\\ w^T{x}_i+b<0,& \text{if yi=−1}(2)\end{array}$$
结合式 (1)，(2) 得
$$y_i(w^T{x}_i+b)\ge 0\text{\hspace{1em}(3)}$$
根据SVM的原理，接下来我们需要计算出离超平面最近的训练样本到超平面的距离。根据点到超平面的距离公式，我们可以得到每个样本点到超平面的距离$d_i$：
$$d_i=\frac{1}{\Vert w\Vert }|w^T{x}_i+b|i=1,2,\cdots ,m$$

最小距离$dist$只与$x_i$相关，即
$$dist=\underset{x_i}{\min }\frac{1}{\Vert w\Vert }|w^T{x}_i+b|i=1,2,\cdots ,m\text{\hspace{1em}(4)}$$

有人可能会问，为什么最小距离不与$w,b$相关呢？这是因为想要在样本当中找到离超平面最近的点，必须得是在同一平面的前提下才行，不然就无法比较样本到超平面的远近了。在超平面固定的情况下，无论$w,b$为何值，最小距离的表示方法都为式(4)。

(P.S 而${\min }_{w,b,x_i}\frac{1}{\Vert w\Vert }|w^T{x}_i+b|$的目的就不是寻找离超平面最近的点了，而是寻找一组$w,b,x_i$，即寻找一个超平面，使得$x_i$这个点到超平面的距离最小。这样的话${\min }_{w,b,x_i}\frac{1}{\Vert w\Vert }|w^T{x}_i+b|$就会等于0，因为一定会存在无数个超平面，使得这个点到超平面的距离为0。因此${\min }_{w,b,x_i}\frac{1}{\Vert w\Vert }|w^T{x}_i+b|$不是我们目标的数学表达形式。)

根据式(3)，可以将上式改写为
$$\underset{x_i}{\min }\frac{1}{\Vert w\Vert }{y}_i(w^T{x}_i+b)i=1,2,\cdots ,m\text{\hspace{1em}(5)}$$
而对于同一个超平面，它的参数$w,b$是不确定的。假设有一平面$x_1+3x_2+2x_3-4=0$，接下来将两边同时乘2,，得平面$2x_1+6x_2+4x_3-8=0$。虽然它们的参数不同，但却是同一个平面。所以对于之后得出的最优超平面方程来说，有无数组成比例的参数$w,b$符合条件，而我们只需要确定一个即可。

为了方便计算，我们令$\min y_i(w^T{x}_i+b)=1$。这个约束的言外之意就是在计算最近的样本到超平面距离时，存在唯一的$w,b$，使得所使用的距离公式的分子部分等于1。

（1）为什么这个约束能使$w,b$唯一呢？

因为超平面已经固定，所以无数组$w,b$是线性成比例的，要想继续保证超平面固定，$w,b$只能成比例改变，也就是说只允许$w,b$乘上一个相同的数，即$\xi w^{T}x+\xi b$。假设现在有一组$w,b$满足上述约束，即把最近的样本$(x_i,y_i)$代入超平面方程后，得$y_i(w^T{x}_i+b)=1$，若想寻找其他满足约束的$w,b$，我们首先需将$w,b$成比例变换，即$y_i(\xi w^T{x}_i+\xi b)=1$，将$\xi$提到外面，得$\xi y_i(w^T{x}_i+b)=1$，由于$y_i(w^T{x}_i+b)=1$，所以$\xi =1$。因此其他满足约束的$\xi w,\xi b$其实就是原来的$w,b$，即这个约束能使$w,b$唯一。

（2）为什么$\min y_i(w^T{x}_i+b)$对应的是最近样本到超平面距离公式的分子呢？

距离公式的分子的大小也能反映出样本到超平面的远近，分子越小，样本点离超平面越近。所以能得到最小的分子就意味着它是离超平面最近的点。

(上面说的有点啰嗦，以便未来失忆的自己能够回忆起这些苦思冥想出来的细节，哈哈哈)

由于最小距离与$w,b$无关，式(5)可改写为
$$\frac{1}{\Vert w\Vert }\underset{x_i}{\min }{y}_i(w^T{x}_i+b)i=1,2,\cdots ,m\text{\hspace{1em}(6)}$$

又因为$\min y_i(w^T{x}_i+b)=1$，所以最小距离$dist$可表示为
$$dist=\frac{1}{\Vert w\Vert }$$

我们需要找到一个超平面，使得$dist$最大，即
$$\begin{array}{rl}\underset{w,b}{\max }& \frac{1}{\Vert w\Vert }\\ \text{s.t. }& y_i(w^T{x}_i+b)\ge 0i=1,2,\cdots ,m\\ & \min y_i(w^T{x}_i+b)=1i=1,2,\cdots ,m\end{array}$$
上式等价于
$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}{w}^{T}w\\ \text{s.t. }& 1-y_i(w^T{x}_i+b)\le 0i=1,2,\cdots ,m\end{array}\text{\hspace{1em}(7)}$$
这是一个带约束的二次凸优化问题，我们一般用拉格朗日乘子法解决此类问题。

2.1 拉格朗日乘子法

下面用一个二维的例子来说明：

黑色虚线代表待优化函数$f(x)$的等高线，中心为函数的最小值，红色实线为约束条件$h(x)$。我们需要在这条红线上找到一个点来满足$f(x)$最小。在左图中，使得$f(x)$最小的点是$x_1$，在点$x_1$处$f(x)$一定与$h(x)$相切。如果在$x_1$处$f(x)$与$h(x)$相交，如右图所示，则$x_1$一定不是最小值处，因为$h(x)$是连续的，所以一定可以找到其他的点，如点$x_2$，使得$f(x_2)<f(x_1)$。

设极小值点为$x^{\ast }$，在$x^{\ast }$处，$f(x)$与$h(x)$相切，这就意味着$\nabla f(x^{\ast })$与$\nabla h(x^{\ast })$平行，即存在$\lambda \ne 0$，使得
$$\nabla f(x^{\ast })+\lambda \nabla h(x^{\ast })=0\text{\hspace{1em}(8)}$$
定义拉格朗日函数$\mathcal{L}(x,\lambda )$为
$$\mathcal{L}(x,\lambda )=f(x)+\lambda h(x)$$
对$\mathcal{L}(x,\lambda )$中的$x,\lambda$求偏导后分别等于0，就得到了式(8)与约束条件$h(x)=0$。

2.2 KKT条件

上述解决的是带等式约束的优化问题，而对于不等式约束的优化，则需要满足额外的条件。

假设我们的优化问题为
$$\begin{array}{rl}\underset{x}{\min }& f(x)\\ \text{s.t. }& g_i(x)\le 0,i=1,2,\cdots ,m\\ & h_j(x)=0,j=1,2,\cdots ,n\end{array}$$

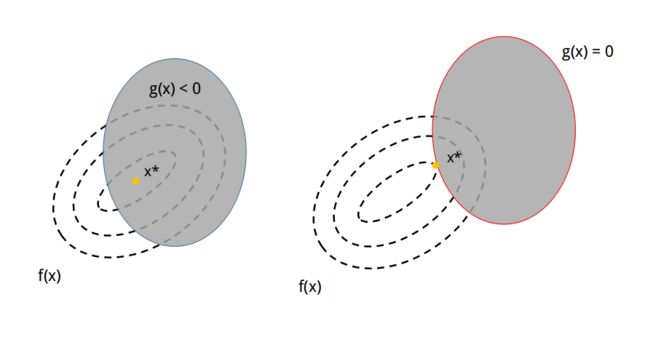
上图中灰色区域表示约束条件$g_i(x)\le 0$的范围，也就是说最后找到的最小值必须落在灰色区域中。设$x^{\ast }$为最小值处，我们分两种情况讨论：

(1) 最小值落在了$g(x)<0$ 区域中（左图）。这种情况意味着约束条件根本没有起作用，不管有没有这个约束条件，最后$x^{\ast }$的位置都是相同的。所以这种情况等同于最小化$f(x)$时没有$g(x)\le 0$这个约束，此时在式(8)上等同于$\lambda =0$。
(2) 最小值落在了$g(x)=0$上（右图）。这种情况与等式约束类似，不同的是$f(x)$与$g(x)$在最小值处的梯度一定是相反的。这是因为$f(x)$等高线的值越往中心越小，所以在$x^{\ast }$处，$\nabla f(x^{\ast })$是朝向灰色区域的；而对于$g(x)$，灰色区域小于0，灰色区域外大于0，所以$\nabla g(x^{\ast })$方向是朝向灰色区域外的。因此，$\nabla f(x^{\ast })$与$\nabla g(x^{\ast })$是相反的，此时在式(8)上等同于$\lambda >0$。

综合上述两种情况，得
$$\{\begin{array}{ll}\lambda >0,& \text{if g(x∗)=0}\\ \lambda =0,& \text{if g(x∗)<0}\end{array}$$
则
$$\{\begin{array}{l}\lambda \ge 0\\ \lambda g(x^{\ast })=0(9)\end{array}$$

式(9)被称作互补松弛条件（complementary slackness）。

构造拉格朗日函数
$$\mathcal{L}(x,\alpha ,\beta )=f(x)+\sum _{i=1}^m{\alpha }_i{g}_i(x)+\sum _{j=1}^n{\beta }_j{h}_j(x)$$
其中最优解$x^{\ast }$满足KKT条件：
$$\{\begin{array}{l}{g}_i(x^{\ast })\le 0\\ h_j(x^{\ast })=0\\ {\alpha }_i\ge 0\\ {\alpha }_i{g}_i(x^{\ast })=0\end{array}$$
回到硬间隔SVM的优化问题，构造拉格朗日函数$\mathcal{L}(w,b,\alpha )$为
$$\mathcal{L}(w,b,\alpha )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))i=1,2,\cdots ,m\text{\hspace{1em}(10)}$$
其最优解满足KKT条件：
$$\{\begin{array}{ll}1-y_i(w^T{x}_i+b)\le 0& i=1,2,\cdots ,m\\ {\alpha }_i\ge 0& i=1,2,\cdots ,m\\ {\alpha }_i(1-y_i(w^T{x}_i+b))=0& i=1,2,\cdots ,m\end{array}\text{\hspace{1em}(11)}$$
接下来可以对拉格朗日函数$\mathcal{L}(w,b,\alpha )$求导并解方程组，求出超平面的参数。然而，在现实中，我们很有可能会遇到数量很多、维度很高的样本，此时求导的方法会变得很慢。为了解决这个问题，我们可以把原始问题转化为对偶问题。通过求解对偶问题，得到超平面的参数。

2.3 对偶问题

首先将带约束优化问题的式(7)转化为无约束问题，那么式(7)等价于下面式子：
$$\begin{array}{rl}\underset{w,b}{\min }\underset{\alpha }{\max }& \mathcal{L}(w,b,\alpha )\\ \text{s.t. }& {\alpha }_i\ge 0i=1,2,\cdots ,m\end{array}\text{\hspace{1em}(12)}$$
且式(12)满足式(7)的约束。

为了解释它们为什么等价，下面分两种情况讨论：

(1) 当式(12)中参数不满足式(7)约束。

此时，存在$i\in 1,2,\cdots ,m$，使得$1-y_i(w^T{x}_i+b)>0$，而${\alpha }_i\ge 0$，所以${\max }_{\alpha }\mathcal{L}(w,b,\alpha )=+\infty$。

(2) 当式(12)中参数满足式(7)约束。

此时，$1-y_i(w^T{x}_i+b)\le 0,i=1,2,\cdots ,m$，而${\alpha }_i\ge 0$，所以${\max }_{\alpha }\mathcal{L}(w,b,\alpha )=\frac{1}{2}{w}^{T}w$。

综合上述两种情况
$$\{\begin{array}{l}{\max }_{\alpha }\end{array}$$