MATLAB学习笔记2:MATLAB基础知识(下)
阅读前请注意:
1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录,是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 @K2SO4钾 撰写、编辑,发布于 @K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协会CSDN官方账号 @CCNU_HelloWorld 。注意,如需转载需得到作者 @K2SO4钾 的同意与授权!
2. 学习笔记基于 《MATLAB R2018a完全自学一本通》(刘浩, 韩晶) 1 ,笔记中增加了很多程序示例和笔者个人的思考。学习笔记面向刚接触MATLAB的新手,内容偏基础。笔记中示例用MATLAB版本为MATLAB R2019a。
3. 请谅解笔记可能会出现的错误,欢迎指正讨论;由于MATLAB更新导致的旧代码无法使用的情况,也欢迎讨论交流。
快速跳转: 直接开始阅读 跳转到博客一半位置 跳转到思考题 作者栏与参考文献
上一篇:
下一篇:
文章目录
-
- 2.0 MATLAB学习笔记:传送门汇总
-
- 2.0.1 MATLAB学习笔记:传送门汇总
- 2.0.2 MATLAB拓展学习:传送门汇总
- 2.0.3 MATLAB深入学习:传送门汇总
- 2.0.4 MATLAB应用实例:传送门汇总
- 2.2 运算符与运算函数
-
- 2.2.1 运算符
-
- 2.2.1.1 算术运算符
- 2.2.1.2 关系运算符
- 2.2.1.3 逻辑运算符
- 2.2.1.4 MATLAB提供的常量
- 2.2.2 常用符号
-
- 2.2.2.1 常用符号及其常用用法
- 2.2.2.2 设置字符串和字符向量的格式的相关符号(了解)
- 2.2.3 常用运算函数
-
- 2.2.3.1 基本算术函数
- 2.2.3.2 指数和对数函数
- 2.2.3.3 离散数学函数
- 2.2.3.4 线性代数与统计函数
- 2.2.3.5 三角数学函数
- 2.2.3.6 部分特殊函数(了解)
- 2.2.4 运算符优先级
- 2.3 矩阵基础
-
- 2.3.1 向量
- 2.3.2 数组与矩阵
-
- 2.3.2.1 数组与矩阵
- 2.3.2.2 矩阵的创建
- 2.3.2.3 获取矩阵基本信息
- 2.3.2.4 访问矩阵元素
- 2.3.2.5 矩阵的基本操作
- 2.3.2.6 查找矩阵中的元素
- 思考题2
2.0 MATLAB学习笔记:传送门汇总
2.0.1 MATLAB学习笔记:传送门汇总
MATLAB学习笔记0:学习须知
MATLAB学习笔记1:MATLAB概述
MATLAB学习笔记2:MATLAB基础知识(上)
MATLAB学习笔记2:MATLAB基础知识(中)
MATLAB学习笔记3:MATLAB编程基础(前半)
MATLAB学习笔记3:MATLAB编程基础(后半)
MATLAB学习笔记5:绘图基础与数据可视化(上)
MATLAB学习笔记5:绘图基础与数据可视化(中)
2.0.2 MATLAB拓展学习:传送门汇总
MATLAB拓展学习T1:匿名函数和内联函数
MATLAB拓展学习T2:程序性能优化技术
MATLAB拓展学习T3:histogram函数详解
MATLAB拓展学习T4:数据导入与查表技术
内容施工中~~
2.0.3 MATLAB深入学习:传送门汇总
MATLAB深入学习S1:数字滤波技术的MATLAB实现
MATLAB深入学习S2:元胞自动机原理及MATLAB实现
MATLAB深入学习S3:图像处理技术
内容施工中~~
2.0.4 MATLAB应用实例:传送门汇总
MATLAB应用实例Y1:Floyd算法
内容施工中~~
2.2 运算符与运算函数
2.2.1 运算符
MATLAB中的运算符是一些符号,它们告诉编译器执行特定的数学或逻辑操作。运算符是 MATLAB 运行代码、执行运算功能的基础,因此必须牢牢掌握。
2.2.1.1 算术运算符
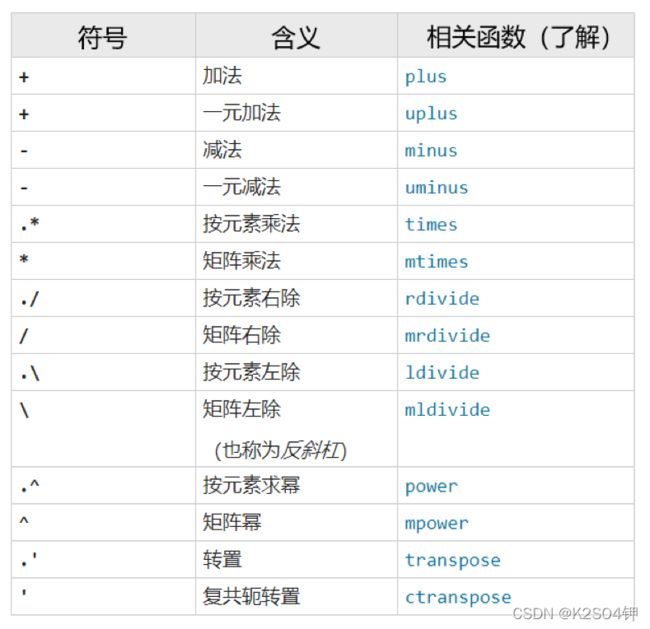
算术运算符是最常用的运算符之一,MATLAB 中最基础的运算依靠的就是算术运算符。下面表格中的每个符号都需要理解其含义并灵活运用(部分符号将在学习笔记4:矩阵中讲到),相关函数一列是对应符号的底层函数,仅需了解。
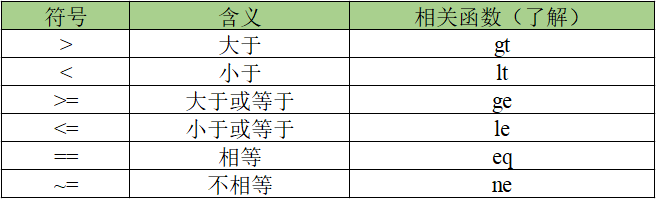
2.2.1.2 关系运算符
关系运算符的使用方法已经在MATLAB学习笔记2:MATLAB基础知识(上)中介绍过,这里不再赘述。
2.2.1.3 逻辑运算符
逻辑运算符的使用方法已经在MATLAB学习笔记2:MATLAB基础知识(上)中介绍过,这里不再赘述。
2.2.1.4 MATLAB提供的常量
这些常量可以在 MATLAB 中直接使用。如果常量与其它已设的变量重名,则变量的值将覆盖常量的值,在清除工作区该变量之后,常量的值恢复为预设。因此建议为变量命名时避开常量。
2.2.2 常用符号
2.2.2.1 常用符号及其常用用法
下面列出了MATLAB中经常使用的符号以及它们的基础用法。这里仅列出了这些符号的基础用法,在基础学习阶段,下面这些用法我们都会学习到(除了 ! 调用操作系统命令之外)。
需要注意的是,不同编程语言当中符号的用法不尽相同,在学习时应该去找到不同语言之间的符号使用的关联,并将不一样的符号用法加以区分。
在MATLAB符号中,一些符号经常会被混用,从而导致代码报错或产生错误的结果。按照笔者的经验,索引时 ( ) 和 { } 容易混淆,使用字符数组和字符串时 ’ ’ 和 " " 容易混淆,使用逻辑非时 ~ 常被写成 ! (C语言习惯)等。
2.2.2.2 设置字符串和字符向量的格式的相关符号(了解)
下面这些符号可以用于 设置字符串和字符向量的格式。在这些符号的帮助下,字符串和字符向量不仅可以灵活地表达各种形式的文本,还可以避免文本和常用符号而引起的冲突。在使用fprintf、compose、sprintf、error等需要使用文本的函数,在字符串或字符向量中使用这些符号可以达到相应的文本效果。
其中最需要的是换行符\n。
☆ 例2-10: 编写程序,使命令行窗口输出如下文本:
分析:
clc,clear all,close all
fprintf('%% %% %% %% %% %% %% %% %% %% %%\n')
fprintf('%% \\ ''Hello World'' / %%\n')
fprintf('%% %% %% %% %% %% %% %% %% %% %%\n')
2.2.3 常用运算函数
MATLAB中提供了大量的运算函数,很多函数我们经常用到,其中的 基本算术函数是最基础的运算函数。使用这些函数能避免繁杂的程序设计,很多函数需要我们牢记并掌握。一些函数会在后续的章节中讲到,在基础学习阶段仅需了解的函数已用 * 标出。
2.2.3.1 基本算术函数
标注 # 的函数非常重要,在整个基础学习过程中会经常遇到,需要牢记并会灵活使用,否则在写相关表达式的代码或进行基础的算术运算时可能会出现问题。
| 基本算术函数 | 含义 |
|---|---|
| # sum | 求数组或矩阵第一维度总和 |
| * cumsum | 求数组或矩阵第一维度累积和 |
| * movsum | 求数组或矩阵第一维度在某个设定窗口下的移动总和 |
| prod | 求数组或矩阵第一维度的积 |
| * cumprod | 求数组或矩阵第一维度累积的乘积 |
| * movprod | 求数组或矩阵第一维度在某个设定窗口下的移动总积 |
| # abs | 取绝对值 |
| diff | 求差分和近似的导数 |
| trapz | 求数组的梯形数值积分 |
| conv | 求卷积 |
| * uminus | 一元减法(即矩阵取负) |
| * uplus | 一元加法(即矩阵取正) |
| # mod | 求除运算后的余数(取模),r = mod(a,b)即r = a-b.*floor(a./b) |
| rem | 求除运算后的余数(取模),r = rem(a,b)即r = a-b.*fix(a./b) |
| * idivide | 带有舍入选项的整除 |
| # ceil | 取整函数,向正无穷舍入 |
| # fix | 取整函数,向零舍入 |
| # floor | 取整函数,向负无穷舍入 |
| # round | 取整函数,四舍五入为最近的小数或整数 |
2.2.3.2 指数和对数函数
标注 # 的函数非常重要,在整个基础学习过程中会经常遇到,需要牢记并会灵活使用,否则在写相关表达式的代码或进行基础的算术运算时可能会出现问题。
| 指数和对数 | 含义 |
|---|---|
| # exp | 指数函数,即 e x e^{x} ex |
| * expm1 | 针对x值较小时 e x − 1 e^{x}-1 ex−1的精确值 |
| # log | 自然对数函数,即 l n ( x ) ln(x) ln(x) |
| # log10 | 以10为底的对数,即 l g ( x ) lg(x) lg(x) |
| log2 | 以2为底的对数,即 l o g 2 x log_{2}^{x} log2x |
| * log1p | 针对x值较小时的 l o g ( x + 1 ) log(x+1) log(x+1)的精确值 |
| * pow2 | 求以2为底的幂值,即 2 x 2^{x} 2x对浮点数字进行缩放(其它底数的幂值请使用 ^ 和 .^) |
| # sqrt | 求算术平方根,即 x \sqrt{x} x,或 x 1 2 x^{\frac{1}{2}} x21 |
| sqrtm | 求矩阵平方根,即已知X*X = A,求X |
| * nextpow2 | 求2的更高次幂的指数,y = nextpow2(x)即求 x ⩽ 2 y x \leqslant 2^{y} x⩽2y的最小y值 |
| nthroot | 求实数的n次实根,nthroot(X,N)即求 X N \sqrt[N]{X} NX |
2.2.3.3 离散数学函数
| 离散数学函数 | 含义 |
|---|---|
| factor | factor(n),返回包含n的质因数的行向量 |
| factorial | 求阶乘 |
| gcd | gcd(A,B),求A、B的最大公约数 |
| lcm | lcm(A,B),求A、B的最小公倍数 |
| * isprime | 判断矩阵中元素是否为质数 |
| * perms | 求元素所有可能的矩阵排列 |
| nchoosek | nchoosek(n,k),求 C n k = n ! ( n − k ) ! k ! C_{n}^{k}=\frac{n!}{(n-k)! k!} Cnk=(n−k)!k!n! |
2.2.3.4 线性代数与统计函数
这些函数将在学习矩阵、学习数值运算时讲到。标注 # 的函数非常重要,在整个基础学习过程中会经常遇到,需要牢记并会灵活使用,具体使用方法可以参考帮助文档。
| 线性代数与统计函数 | 含义 |
|---|---|
| # mean | 求平均值 |
| # median | 求中位数 |
| # min | 求最小值 |
| # max | 求最大值 |
| corrcoef | 求两个向量的相关系数 |
| var | 求方差 |
| std | 求标准差 |
| cov | 求协方差 |
| corr | 求相关系数 |
| rank | 求矩阵的秩 |
2.2.3.5 三角数学函数
需要注意的是有些三角数学函数的输入参数只能是弧度值或角度值,此时需要使用弧度-角度转化函数进行转化后再代入函数中运算。三角数学函数都有一定的命名规律,因此无需刻意记忆。
| 正弦函数 | 含义 |
|---|---|
| sin | 以弧度为单位,求输入参数的正弦值 |
| * sind | 以角度为单位,求输入参数的正弦值 |
| asin | 以弧度为单位,求输入参数的反正弦值 |
| * asind | 以角度为单位,求输入参数的反正弦值 |
| sinh | 求输入参数的双曲正弦值 |
| asinh | 求输入参数的反双曲正弦值 |
| 余弦函数 | 含义 |
|---|---|
| cos | 以弧度为单位,求输入参数的余弦值 |
| * cosd | 以角度为单位,求输入参数的余弦值 |
| acos | 以弧度为单位,求输入参数的反余弦值 |
| * acosd | 以角度为单位,求输入参数的反余弦值 |
| cosh | 求输入参数的双曲余弦值 |
| acosh | 求输入参数的反双曲余弦值 |
| 正切函数 | 含义 |
|---|---|
| tan | 以弧度为单位,求输入参数的正切值 |
| * tand | 以角度为单位,求输入参数的正切值 |
| atan | 以弧度为单位,求输入参数的反正切值 |
| * atand | 以角度为单位,求输入参数的反正切值 |
| tanh | 求输入参数的双曲正切值 |
| atanh | 求输入参数的反双曲正切值 |
| * atan2 | 求四象限的反正切值 |
| 余割函数 | 含义 |
|---|---|
| csc | 以弧度为单位,求输入参数的余割值 |
| * cscd | 以角度为单位,求输入参数的余割值 |
| acsc | 以弧度为单位,求输入参数的反余割值 |
| * acscd | 以角度为单位,求输入参数的反余割值 |
| csch | 求输入参数的双曲余割值 |
| acsch | 求输入参数的反双曲余割值 |
| 正割函数 | 含义 |
|---|---|
| sec | 以弧度为单位,求输入参数的正割值 |
| * secd | 以角度为单位,求输入参数的正割值 |
| asec | 以弧度为单位,求输入参数的反正割值 |
| * asecd | 以角度为单位,求输入参数的反正割值 |
| sech | 求输入参数的双曲正割值 |
| asech | 求输入参数的反双曲正割值 |
| 余切函数 | 含义 |
|---|---|
| cot | 以弧度为单位,求输入参数的余切值 |
| * cotd | 以角度为单位,求输入参数的余切值 |
| acot | 以弧度为单位,求输入参数的反余切值 |
| * acotd | 以角度为单位,求输入参数的反余切值 |
| coth | 求输入参数的双曲余切值 |
| acoth | 求输入参数的反双曲余切值 |
| 斜边函数 | 含义 |
|---|---|
| * hypot | hypot(a,b),求直角三角形直角边为a、b的斜边长 |
| 转换函数 | 含义 |
|---|---|
| deg2rad | 将角从以度为单位转换为以弧度为单位 |
| rad2deg | 将角的单位从弧度转换为度 |
2.2.3.6 部分特殊函数(了解)
本小节介绍的函数是MATLAB中已有的一些处理数论、信号与系统相关问题的函数。这些函数为用户提供了极大的便利,用户无需再自行实现一些复杂函数的代码,调用函数时非常方便。这一小节仅供了解,基础学习阶段不要深究。
| 信号与系统相关函数 | 含义 |
|---|---|
| dirac | 狄拉克 δ ( t ) \delta (t) δ(t)函数 |
| heaviside | 阶跃函数,即 ∫ − ∞ + ∞ δ ( t ) d t \int_{-\infty }^{+\infty}\delta (t)dt ∫−∞+∞δ(t)dt |
| rectangularPulse | rectangularPulse(a,b,x),矩形脉冲函数 |
| triangularPulse | triangularPulse(a,b,c,x),三角脉冲函数 |
| sign | 符号函数,即 s g n ( x ) = { 1 , x > 0 0 , x = 0 − 1 , x < 0 sgn(x) = \left\{\begin{matrix}1, x>0\\0 , x=0\\-1 ,x<0\end{matrix}\right. sgn(x)=⎩⎨⎧1,x>00,x=0−1,x<0 |
| 复变函数与数论 | 含义 |
|---|---|
| beta | β \beta β函数,即 β ( x , y ) = ∫ 0 1 t x − 1 ( 1 − t ) y − 1 d t \beta(x,y) = \int_{0}^{1}t^{x-1}(1-t)^{y-1}dt β(x,y)=∫01tx−1(1−t)y−1dt |
| gamma | 勒让德函数,即 Γ ( x ) = ∫ 0 + ∞ e − t t x − 1 d t \Gamma (x) = \int_{0}^{+\infty }e^{-t}t^{x-1}dt Γ(x)=∫0+∞e−ttx−1dt |
| legendre | 关联勒让德函数,即 P l m ( x ) = ( − 1 ) m ( 1 − x 2 ) m 2 d m d x m P l ( x ) P_{l}^{m}(x)=(-1)^m(1-x^2)^{\frac{m}{2}}\frac{d^m}{dx^m}P_l(x) Plm(x)=(−1)m(1−x2)2mdxmdmPl(x),其中 P l ( x ) = 1 2 l l ! d l d x l ( x 2 − 1 ) l P_l(x)=\frac{1}{2^{l}l!}\frac{d^{l}}{dx^{l}}(x^2-1)^l Pl(x)=2ll!1dxldl(x2−1)l |
| zeta | 黎曼-泽塔函数,即 ζ ( s ) = ∑ n = 1 + ∞ 1 n s \zeta(s)=\sum_{n=1}^{+\infty }\frac{1}{n^{s}} ζ(s)=∑n=1+∞ns1 |
| psi | digamma函数,即 ψ ( z ) = Γ ′ ( z ) Γ ( z ) = − γ − 1 z + ∑ k = 1 + ∞ ( 1 k − 1 k + z ) \psi (z)=\frac{\Gamma '(z)}{\Gamma (z)}=-\gamma -\frac{1}{z}+\sum_{k=1}^{+\infty }(\frac{1}{k}-\frac{1}{k+z}) ψ(z)=Γ(z)Γ′(z)=−γ−z1+∑k=1+∞(k1−k+z1),其中 ψ ( 1 ) = − γ ≈ − 0.5772 \psi(1)=-\gamma \approx -0.5772 ψ(1)=−γ≈−0.5772;digamma的及其各阶导数为polygamma函数,即 ψ ( k ) ( z ) = d k d s k ψ ( 0 ) ( z ) = ( − 1 ) k + 1 ∑ m = 1 + ∞ k ! ( m + z ) k + 1 \psi ^{(k)}(z)=\frac{d^{k}}{ds^{k}}\psi^{(0)}(z)=(-1)^{k+1}\sum_{m=1}^{+\infty}\frac{k!}{(m+z)^{k+1}} ψ(k)(z)=dskdkψ(0)(z)=(−1)k+1∑m=1+∞(m+z)k+1k! |
| polylog | polylog函数,即 L i ( s , z ) = ∑ k = 1 + ∞ z k k s Li(s,z) =\sum_{k=1}^{+\infty }\frac{z^{k}}{k^{s}} Li(s,z)=∑k=1+∞kszk, s , z ∈ C s,z\in \mathbb{C} s,z∈C, ∣ z ∣ < 1 \begin{vmatrix}z\end{vmatrix}<1 ∣∣z∣∣<1 ,其与zeta函数的关系式: L i ( s , 1 ) = ∑ k = 1 + ∞ 1 k s = ζ ( s ) Li(s,1)=\sum_{k=1}^{+\infty }\frac{1}{k^{s}}=\zeta(s) Li(s,1)=∑k=1+∞ks1=ζ(s),其递推式: L i ( s + 1 , z ) = ∫ 0 z L i ( s , t ) t d t Li(s+1,z)=\int_{0}^{z}\frac{Li(s,t)}{t}dt Li(s+1,z)=∫0ztLi(s,t)dt |
| hurwitzZeta | Hurwitz zeta函数,即 ζ ( s , α ) = ∑ n = 0 + ∞ 1 ( n + a ) s \zeta(s,\alpha)=\sum_{n=0}^{+\infty}\frac{1}{(n+a)^{s}} ζ(s,α)=∑n=0+∞(n+a)s1 |
| dilog | dilog函数,即 d i l o g ( x ) = ∫ 1 x l n ( t ) 1 − t d t dilog(x)=\int_{1}^{x}\frac{ln(t)}{1-t}dt dilog(x)=∫1x1−tln(t)dt,有时在数值运算结果中出现 |
| eulergamma | 欧拉-马斯克若尼常数(欧拉常数), γ = − ψ ( 1 ) ≈ 0.57722 \gamma = -\psi(1) \approx 0.57722 γ=−ψ(1)≈0.57722,可使用double将其转化为双精度类型 |
| residue(工具箱) | [r, p]=residue(a, b),求函数的留数、极点,a、b分别为分子多项式、分母多项式的系数矩阵 |
| airy | airy函数,即 A k ( z , p , q ) = 1 2 π j ∫ L k t − p ( l n t ) q e z t − t 3 3 d t A_k(z,p,q)=\frac{1}{2\pi j}\int _{L_k}t^{-p}(lnt)^q e^{zt-\frac{t^3}{3}}dt Ak(z,p,q)=2πj1∫Lkt−p(lnt)qezt−3t3dt,MATLAB中airy函数默认 p = q = 0 p=q=0 p=q=0 |
| besselj | 第一类贝塞尔函数,即 x 2 d 2 y d x 2 + x d y d x + ( x 2 − a 2 ) y = 0 x^{2}\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}+(x^{2}-a^{2})y=0 x2dx2d2y+xdxdy+(x2−a2)y=0的标准解函数 y ( x ) = c 1 J α ( x ) + c 2 Y α ( x ) y(x)=c_1 J_{\alpha}(x)+c_2 Y_{\alpha}(x) y(x)=c1Jα(x)+c2Yα(x)中的第一类贝塞尔函数: J α ( x ) = ∑ m = 0 + ∞ ( − 1 ) m m ! Γ ( m + α + 1 ) ( 1 2 x ) 2 m + α J_{\alpha}(x)=\sum_{m=0}^{+\infty}\frac{(-1)^m}{m!\Gamma (m+\alpha+1)}(\frac{1}{2}x)^{2m+\alpha} Jα(x)=∑m=0+∞m!Γ(m+α+1)(−1)m(21x)2m+α |
| bessely | 第二类贝塞尔函数,即 x 2 d 2 y d x 2 + x d y d x + ( x 2 − a 2 ) y = 0 x^{2}\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}+(x^{2}-a^{2})y=0 x2dx2d2y+xdxdy+(x2−a2)y=0的标准解函数 y ( x ) = c 1 J α ( x ) + c 2 Y α ( x ) y(x)=c_1 J_{\alpha}(x)+c_2 Y_{\alpha}(x) y(x)=c1Jα(x)+c2Yα(x)中的第二类贝塞尔函数: Y α ( x ) = J α ( x ) c o s ( α π ) − J − α ( x ) s i n ( α π ) Y_{\alpha}(x)=\frac{J_{\alpha}(x)cos(\alpha \pi)-J_{-\alpha}(x)}{sin(\alpha \pi)} Yα(x)=sin(απ)Jα(x)cos(απ)−J−α(x) |
| besseli | 修正贝塞尔方程 x 2 d 2 y d x 2 + x d y d x − ( x 2 + ν 2 ) y = 0 x^{2}\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}-(x^{2}+\nu^{2})y=0 x2dx2d2y+xdxdy−(x2+ν2)y=0的基本解中的其中一个,即第一类经过修改的贝塞尔函数 I ν ( x ) = ( 1 2 x ) ν ∑ k = 0 + ∞ ( 1 4 x 2 ) k k ! Γ ( ν + k + 1 ) I_{\nu}(x)=(\frac{1}{2}x)^{\nu}\sum_{k=0}^{+\infty}\frac{(\frac{1}{4}x^2)^k}{k!\Gamma (\nu+k+1)} Iν(x)=(21x)ν∑k=0+∞k!Γ(ν+k+1)(41x2)k,其与 I − ν ( x ) I_{-\nu}(x) I−ν(x)构成修正贝塞尔方程的一组解 |
| besselk | 修正贝塞尔方程 x 2 d 2 y d x 2 + x d y d x − ( x 2 + ν 2 ) y = 0 x^{2}\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}-(x^{2}+\nu^{2})y=0 x2dx2d2y+xdxdy−(x2+ν2)y=0的基本解中的其中一个,即第二类经过修改的贝塞尔函数 K ν ( x ) = ( π 2 ) I − ν ( x ) − I ν ( x ) s i n ( ν π ) K_{\nu}(x)=(\frac{\pi}{2})\frac{I_{-\nu}(x)-I_{\nu}(x)}{sin(\nu\pi)} Kν(x)=(2π)sin(νπ)I−ν(x)−Iν(x) |
| besselh | 第三类贝塞尔函数,即Hankel函数,第一、第二类Hankel函数由第一、第二类贝塞尔函数线性组合定义: { H α ( 1 ) ( x ) = J α ( x ) + i Y α ( x ) H α ( 2 ) ( x ) = J α ( x ) − i Y α ( x ) \left\{\begin{matrix}H_{\alpha}^{(1)}(x)=J_{\alpha}(x)+iY_{\alpha}(x)\\ H_{\alpha}^{(2)}(x)=J_{\alpha}(x)-iY_{\alpha}(x)\end{matrix}\right. {Hα(1)(x)=Jα(x)+iYα(x)Hα(2)(x)=Jα(x)−iYα(x) |
| expint | 计算指数积分,即 E ( x ) = ∫ x + ∞ e − t t d t = − ∫ − ∞ x e t t d t − i π E(x)=\int_{x}^{+\infty}\frac{e^{-t}}{t}dt=-\int_{-\infty}^{x}\frac{e^{t}}{t}dt-i\pi E(x)=∫x+∞te−tdt=−∫−∞xtetdt−iπ(这类积分使用数值积分可能返回不准确的结果) |
| erf | 误差函数,即 ε ( x ) = 2 π ∫ 0 x e − t 2 d t \varepsilon (x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^2}dt ε(x)=π2∫0xe−t2dt |
| ellipj | 返回雅克比(Jacobi)椭圆函数 u = ∫ 0 ϕ d θ 1 − m s i n 2 θ u=\int_{0}^{\phi }\frac{d\theta}{\sqrt{1-msin^2\theta}} u=∫0ϕ1−msin2θdθ的 S N ( u ) = s i n ϕ SN(u)=sin\phi SN(u)=sinϕ、 C N ( u ) = c o s ϕ CN(u)=cos\phi CN(u)=cosϕ、 D N ( u ) = ( 1 − m s i n 2 ϕ ) DN(u)=\sqrt{(1-msin^2\phi)} DN(u)=(1−msin2ϕ) |
2.2.4 运算符优先级
优先级高的运算符总是比优先级低的运算符先运行。MATLAB中的各优先级从 最高到最低 如下:
1. 括号 ()
2. 转置 ( . ′ .' .′)、幂 (.^)、复共轭转置 ( ′ ' ′)、矩阵幂 (^)
3. 带一元减法 (.^-)、一元加法 (.^+) 或逻辑求反 (.^~) 的幂,以及带一元减法 (^-)、一元加法 (^+) 或逻辑求反 (^~) 的矩阵幂(均为从右至左运行)
4. 一元加法 (+)、一元减法 (-)、逻辑求反 (~)
5. 乘法 ( . ∗ .* .∗)、矩阵乘法 ( ∗ * ∗)、右除 (./)、左除 (.)、矩阵右除 (/)、矩阵左除 ()
6. 加法 (+)、减法 (-)
7. 冒号运算符 (: )
8. 小于 (<)、小于或等于 (<=)、大于 (>)、大于或等于 (>=)、等于 (==)、不等于 (~=)
9. 按元素 AND (&)
10. 按元素 OR (|)
11. 短路 AND (&&)
12. 短路 OR (||)
小括号 ‘( )’ 可以覆盖符号的优先级,因此合理运用小括号能避免优先级混乱带来的问题。
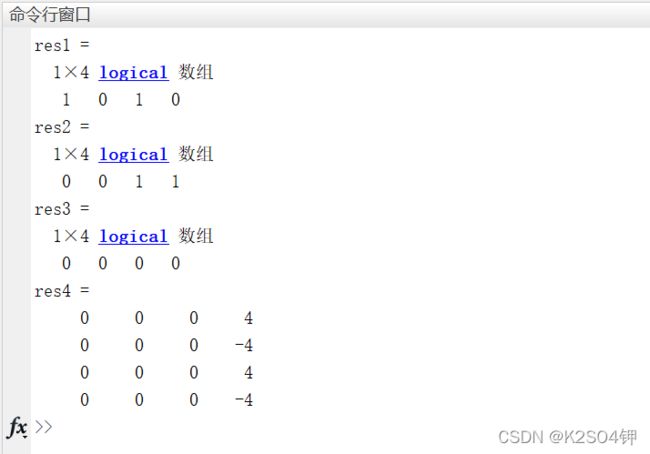
☆ 例2-11: 运行下面的代码前,请自行分析res1-res4的结果,再运行代码对比运行结果与你的分析结果是否相符。
clc,clear all,close all
a = [1 -1 1 -1];
b = [0 0 0 -2];
c = [1 0 1 1];
d = [0 1 1 0];
res1 = a>=b & a>=0
res2 = b|c&d
res3 = ~a & b
res4 = a'*b.^2
分析: 按照MATLAB运算符的优先级顺序,下面的代码标记出了res1-res4表达式的运算顺序。
clc,clear all,close all
a = [1 -1 1 -1];
b = [0 0 0 -2];
c = [1 0 1 1];
d = [0 1 1 0];
res1 = (a>=b) & (a>=0)
res2 = b|(c&d) % 该优先级规则同样适用于 && 和 || 运算符
res3 = (~a) & b
res4 = (a')*(b.^2)
2.3 矩阵基础
这一节中,我们将介绍 MATLAB 中最基础也最常用的数据结构:矩阵。本节只讲矩阵最基础的知识,目的是为学习笔记4:矩阵做好铺垫。
2.3.1 向量
MATLAB中,仅有一个维度(简单理解就是只有一行或一列)的矩阵被称为向量,仅有一行数据的数组也被成为行向量,仅有一列数据的数组被成为列向量。以 1 ∗ 1 1*1 1∗1的矩阵表示单个实数或复数即是一个标量。
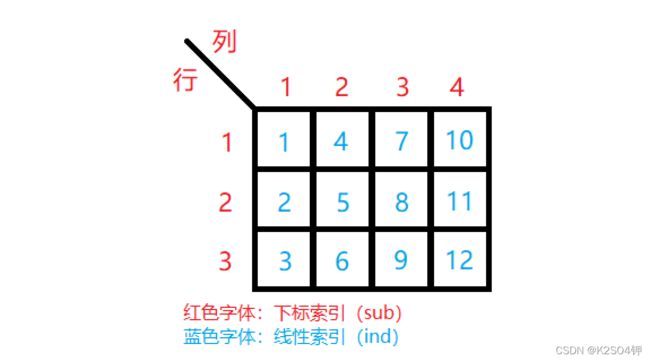
如果用数学语言来描述,定义由 n n n个数 a i ( i = 1 , 2 , . . . , n ) a_{i}(i=1,2, ... , n) ai(i=1,2,...,n)排列成1行 n n n列的矩阵 R = { R 1 R 2 . . . R n } R = \begin{Bmatrix} R_1 & R_2 & ... & R_n \end{Bmatrix} R={R1R2...Rn}即是一个行向量,定义由 n n n个数 a i ( i = 1 , 2 , . . . , n ) a_{i}(i=1,2, ... , n) ai(i=1,2,...,n)排列成 n n n行1列的矩阵 C = { c 1 c 2 . . . c n } C=\begin{Bmatrix} c_1\\ c_2\\ ...\\ c_n \end{Bmatrix} C=⎩⎪⎪⎨⎪⎪⎧c1c2...cn⎭⎪⎪⎬⎪⎪⎫即是一个列向量。
创建一个向量有三种方式,一是使用创建矩阵的方式来创建 (见 2.3.2.2节矩阵的创建 ),二是使用冒号创建一维数组,三是使用一维数组创建函数。
a. 使用冒号创建一维数组
arr = start : step : end:创建一个“第一个元素值为start,每次递增或递减step,直到最后一个元素值为end或者与end的差的绝对值小于等于step”的一维数组(行向量)。如果需要列向量转置即可。若省略step,则step默认为1。
clc,clear all,close all
arr1 = 1:1:6 % 创建一个起始为1、步长为1、终点为1的1*6行向量
arr2 = 1:6 % 与arr1相同
arr3 = 6:-1:1 % 创建一个起始为6、步长为-1、终点为1的1*6行向量
arr4 = (1:2:6)' % 创建一个起始为1、步长为2、终点为6(实际终点为5)的3*1列向量
b. 使用linspace创建一维数组
linspace(start, end, n):创建一个“第一个元素值为start,最后一个元素值为end,元素总数为n且两两之间线性间隔”的一维数组(行向量)。如果需要列向量转置即可。若省略n,则n默认为100。
clc,clear all,close all
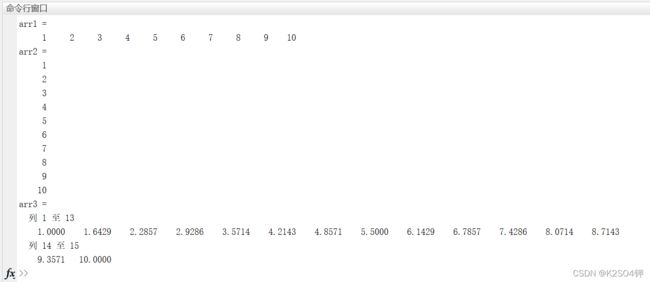
arr1 = linspace(1,10,10) % 创建一个起始为1、终点为10、共有线性间隔10个元素的1*10行向量
arr2 = linspace(1,10,10)' % 创建一个起始为1、终点为10、共有线性间隔10个元素的10*1列向量
arr3 = linspace(1,10,15) % 创建一个起始为1、终点为10、共有线性间隔15个元素的1*15行向量
c. 使用logspace创建一维数组
logspace(start, end, n):创建一个“第一个元素值为 1 0 s t a r t 10^{start} 10start,最后一个元素值为 1 0 e n d 10^{end} 10end,元素总数为n且为等比数列”的一维数组(行向量)。如果需要列向量转置即可。若省略n,则n默认为50。
clc,clear all,close all
arr1 = logspace(1,4,4) % 创建一个起始为10、终点为10000、共4个等比数列元素的1*4行向量
arr2 = logspace(1,4,4)' % 创建一个起始为10、终点为10000、共4个等比数列元素的4*1列向量
arr3 = logspace(1,6,8) % 创建一个起始为10、终点为1000000、共8个等比数列元素的1*8行向量
2.3.2 数组与矩阵
2.3.2.1 数组与矩阵
a. 数组与矩阵的含义
在数学定义中,矩阵是由 m ∗ n m*n m∗n 个数 a i j ( 1 ⩽ i ⩽ m , 1 ⩽ j ⩽ n ) ( i , j , m , n ∈ Z ) a_{ij}(1\leqslant i\leqslant m,1\leqslant j\leqslant n)(i,j,m,n\in \mathbb{Z}) aij(1⩽i⩽m,1⩽j⩽n)(i,j,m,n∈Z) 排成的 m 行 n 列的数表,即: A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots &\vdots & \ddots &\vdots \\ a_{m1}& a_{m2} & \cdots & a_{mn} \end{bmatrix} A=⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎦⎥⎥⎥⎤,A就是一个大小为 m ∗ n m*n m∗n的矩阵。
MATLAB中通常使用数组来区别矩阵。矩阵是数学中(线性代数)的概念,而数组则是计算机的概念。一般来说,数组可以由高维数据组成,也可以存储字符、字符串等;而根据数学定义,矩阵是一个排成的 m 行 n 列的二维数表,其中只能存放数值类型。二维数组就可以理解为矩阵,因此矩阵是数组的子集。
对于数组和矩阵的运算也有区别。对于加法(+)和减法(-),数组和矩阵运算一致;但是对于乘法(*)、左除法(/)、右除法(\)、乘方(^),数组运算是针对两个数组的元素进行运算,而矩阵运算是两个矩阵之间进行运算。这一点将在学习笔记4:矩阵中谈到。
为了方便起见,在本学习笔记中,我们把刚刚谈到的“数组”的概念一律表述为“矩阵”(其实从广义来看二者是一样的),“高维的数组”也将表述为“高维矩阵”。(MATLAB 的“数组”仅是用于区分数学定义下的“矩阵”,但现在 MATLAB 中的“数组”概念一般都会被人们理解为“矩阵”)
b. 矩阵的存储方式
MATLAB 的矩阵并不是以它在命令行窗口展示的方式存储于计算机内存中的,而是 将矩阵中的数据由低维度开始依次存储在一列网格中,每个网格占用计算机的内存与该矩阵的数据类型有关,使用 whos 函数(前几章我们已经讲过 whos 函数的用法)可以快速查看矩阵占用的内存。
上一段话中提及了“维度”的概念。在数学定义中,矩阵中没有“维度”这一概念,维度是线性空间的性质,空间的维度是指空间的基所含向量的个数。MATLAB中引入了“高维矩阵”(也就是“高维数组”)的概念,因此可以把它理解为是一个线性空间。假设一个3行4列的矩阵 A,其大小就是 3 ∗ 4 3*4 3∗4,它的维度就是 2,其中“3行”就是它的第1维度,也就是低维度,“4列”就是它的第2维度,也就是高维度。由此可以类推高维矩阵,例如一个 2 ∗ 3 ∗ 4 ∗ 5 2*3*4*5 2∗3∗4∗5的高维矩阵,2、3、4、5分别就是它的第一、二、三、四维度所包含的向量个数,也就是该维度上的长度。
下面这个例子更直观地展示了矩阵的存储方式:
clc,clear all,close all
fprintf('一个3行4列的矩阵:\n')
A = [1 2 3 4;5 6 7 8;9 10 11 12] % 3行4列的矩阵
fprintf('该矩阵中依次存储的元素:\n')
A(1:end) % 矩阵中依次存储的元素
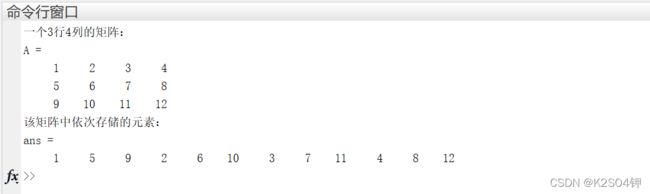
从结果中可以看到,矩阵的存储先从最低维度(行是最低的维度)开始依次存储元素,存储完第一列的所有行时再存储第二列,依此类推。高维矩阵的存储方式也是一样的。
2.3.2.2 矩阵的创建
MATLAB中有两种方式可以创建矩阵。第一种方式是以中括号 [ ] 创建矩阵,第二种方式是使用特殊矩阵的构造函数创建矩阵。本小节我们只讨论第一种方式,第二种方式见学习笔记3:矩阵。
使用中括号 [ ] 可以创建一个二维矩阵。矩阵的列与列之间使用空格或者逗号隔开,行与行之间使用分号或使用换行来隔开。
clc,clear all,close all
A = [1 2 3;4 5 6;7 8 9] % 创建一个3*3的二维矩阵
B = [1,2,3,4
5,6,7,8] % 创建一个2*4的二维矩阵
C = [] % 创建一个空的二维矩阵(矩阵的维度具体详见2.3.2.3节)
细心的同学可能发现了:使用中括号的方式只能用于创建最多二维的矩阵,对于高维矩阵的创建该怎么办呢?对于高维矩阵,中括号的方式不再适用,而是应当采取先使用特殊矩阵的构造函数将高维矩阵初始化,再向矩阵内部填充数据。
高维矩阵在展示时,由于最多只能展示二维矩阵的数据,因此MATLAB会将高维矩阵分割成多个二维矩阵以展示矩阵内的所有元素。
☆ 例2-12: 按要求完成以下任务。
(1)使用任意方法,创建一个3行4列的矩阵,创建一个行向量、一个列向量。这些矩阵中的元素值自拟;
(2)下面这段代码用于创建一个大小 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3、其中元素值均为0的高维矩阵,观察其在MATLAB中的显示;
T2 = zeros(3,3,3)
(3)下面这段代码用于创建一个大小 2 ∗ 2 ∗ 2 ∗ 2 2*2*2*2 2∗2∗2∗2、其中元素值均为0的高维矩阵,观察其在MATLAB中的显示。
T3 = zeros(2,2,2,2)
分析:
clc,clear all,close all
% 第一问
T1_r3c4 = [1 2 3 4;5 6 7 8;9 10 11 12]
T1_r1 = 1:1:10
T1_c1 = [1;2;3;4;5;6]
% 第二问
T2 = zeros(3,3,3)
% 第三问
T3 = zeros(2,2,2,2)
2.3.2.3 获取矩阵基本信息
MATLAB中设置了很多函数,能快速方便地获取矩阵的大小、结构、元素的数据类型等基本信息。
a. 矩阵的大小
矩阵的大小通常由矩阵的维度、每个维度上的长度而定,而这些又决定了矩阵元素的总个数。MATLAB中,通常使用1个函数来查看某个矩阵的维度,2个函数来查看某个矩阵各个维度上的长度,1个函数查看某个矩阵元素的总数量。
ndims(A)(了解):返回矩阵A的维度。需要注意的是,矩阵维数在MATLAB中总是大于等于2(忽略 size(A,dim) = 1 所针对的尾部单一维度),行向量、列向量、空矩阵的维度同样为2,这是因为它们是按照二维矩阵的方式进行存储;
length(A):返回矩阵A最大数组维度的长度,与 max(size(A)) 相同。空矩阵长度为0;
[dim_1, dim_2, … , dim_n] = size(A):返回矩阵A各个维度上的长度,dim_1 至 dim_n 依次为矩阵A在第1维度至第n维度的长度,例如返回一 3 ∗ 4 3*4 3∗4矩阵A的行数与列数即 [row, col] = size(A)。若以 dim = size(A) 的方式调用,则矩阵A各个维度上的长度会以一个行向量存放在 dim 中;
dim = size(A, dim_x):返回矩阵第 dim_x 维上的长度,例如返回一 3 ∗ 4 3*4 3∗4矩阵A的行数(即第一维度)即 dim = size(A, 1);
numel(A)(了解):返回矩阵中所有元素的个数。
clc,clear all,close all
A = rand(4,5); % A为4行5列的矩阵
length_A = length(A) % 返回矩阵最长维度的长度
[row_A,col_A] = size(A) % 返回矩阵行数与列数
ndims_A = ndims(A) % 返回矩阵的维度
numel_A = numel(A) % 返回矩阵元素的个数
————↓———— 提 示 ————↓————
(了解)使用 ndims 函数时需要注意:
- 一维矩阵、空矩阵由于在存储时均按照二维矩阵的方式存储,因此对于它们,ndims函数会返回 2(这也是该函数能返回的最小整数);
- 对于高维矩阵,由于元素删除等原因造成的降维,ndims 函数仍将返回创建该矩阵时矩阵的维度。
clc,clear all,close all
fprintf('原矩阵:\n')
A = rand(2,2,2) % 2*2*2的矩阵
fprintf('原矩阵的维度:\n')
dim_A = ndims(A)
fprintf('\n删除了第一维度的部分信息,导致矩阵A可以看做变成了一个二维矩阵,\n ')
fprintf('但是其实是三维矩阵A的第一维度长度为1(本质上它还是三维矩阵,\n ')
fprintf('并不会因为元素的删除而维度降低):\n ')
A1 = A;
fprintf('矩阵A1:\n')
A1(2,:,:) = []
fprintf('矩阵A1的维度:\n')
dim_A1 = ndims(A1)
fprintf('\n即使将矩阵A中的元素全部删除,ndims函数也返回3\n ')
A2 = A;
fprintf('矩阵A2:\n')
A2(:,:,:) = []
fprintf('矩阵A2的维度:\n')
dim_A2 = ndims(A2)
————↑———————————↑————
b. 矩阵的结构
MATLAB中设置了一些 is 函数来检查矩阵元素的排列方式,即矩阵的结构。如果符合条件,这些 is 函数将返回逻辑1(即逻辑真值),否则将返回逻辑0(即逻辑假值)。下面列出的函数中,isempty 函数需要牢记,其它函数了解即可。
| 函数名称 | 功能 |
|---|---|
| isempty | 检验输入参数是否为空矩阵 |
| isvector | 检验输入参数是否为向量 |
| isscalar | 检验输入参数是否为标量 |
| isrow | 检验输入参数是否为行向量 |
| iscolumn | 检验输入参数是否为列向量 |
| ismatrix | 检验输入参数是否为矩阵 |
| issorted | 检验矩阵在指定维度上是否已排序(升序或降序),调用方式为 issorted(A, dim, ‘direction’) |
| issortedrows | 检验矩阵或表的行是否已排序(升序或降序),调用方式为 issortedrows(A, ‘direction’) |
c. 矩阵元素的数据类型(了解)
MATLAB中设置了一些 is 函数来检查矩阵元素的类型。如果符合条件,这些 is 函数将返回逻辑1(即逻辑真值),否则将返回逻辑0(即逻辑假值)。下面这些函数仅需了解。
| 函数名称 | 功能 |
|---|---|
| isnumeric | 检验输入矩阵的元素是否为数值类型 |
| isinteger | 检验输入矩阵的元素是否为整数型 |
| isfloat | 检验输入矩阵的元素是否为浮点型 |
| isreal | 检验输入矩阵的元素是否为实数 |
| ischar | 检验输入矩阵的元素是否为字符数组类型 |
| islogical | 检验输入矩阵的元素是否为逻辑类型 |
| isstruct | 检验输入参数是否为结构体 |
| iscell | 检验输入参数是否为元胞数组 |
| iscellstr | 检验输入参数是否为字符向量元胞数组 |
2.3.2.4 访问矩阵元素
MATLAB中有两种方式访问矩阵元素,一种是下标寻址,一种是线性寻址。编写程序时,我们一般采用下标寻址,但是对于线性寻址我们也需掌握。
a. 多下标索引(下标寻址)
一个矩阵的各个维度均有一个下标,该矩阵中的某个元素能通过这些下标的组合唯一地标识,这就是多下标索引,也就是 下标寻址。例如一个二维矩阵 A(m,n),对于已知的正整数 i、j( i ⩽ m , j ⩽ n i\leqslant m,j\leqslant n i⩽m,j⩽n),可以唯一确定矩阵中的元素 A(i,j),对于一个三维矩阵就需要三个正整数来确定矩阵中的某个元素,以此类推。对于二维矩阵来说:
A(row_num, col_num):访问矩阵A第 row_num 行第 col_num 列的元素。
b. 单下标线性索引(线性寻址)
按照 MATLAB 在内存空间中存储矩阵的方法 ,矩阵的各个元素从第一个元素开始依次编号,这样的编号成为单下标,通过矩阵单下标访问矩阵元素的方式称为 线性寻址。例如一个二维矩阵 A(m,n),对于已知的正整数 ( i ⩽ m ∗ n ) (i\leqslant m*n) (i⩽m∗n),可以唯一确定矩阵中的元素 A(i),对于一个高维矩阵中的每个元素来说同样有唯一的单下标。对于一个二维矩阵来说:
A(linear_add_ind):访问矩阵A线性寻址下标为 linear_add_ind 的元素。
c. 单下标线性索引和多下标索引之间的转换
通过 ind2sub 函数和 sub2ind 函数能快速实现单下标线性索引和多下标索引之间的转换。
sub2ind(size_A, sub_1, sub_2, …):将下标索引转换为线性索引。size_A是矩阵各个维度的长度,即 size(A);输入参数 sub_1 等表示各个维度上的下标索引;该函数返回值为线性索引,为一个整数。
[sub_1, sub_2, …] = ind2sub(size_A, ind):将线性索引转换为下标索引。size_A是矩阵各个维度的长度,即 size(A);输入参数 ind 表示线性索引,为一个整数;该函数返回线性索引对应的下标索引,各个维度上的下标索引分别存储于 sub_1, sub_2, … 。
考虑一个二维矩阵 A(m, n),将下标索引 A(sub1, sub2) 转化为线性索引的公式为: i n d = ( s u b 2 − 1 ) ∗ m + s u b 1 ind=(sub2-1)*m+sub1 ind=(sub2−1)∗m+sub1 。
对于二维矩阵,单下标线性索引和多下标索引之间的转换原理需要清楚,而对于高维矩阵则仅需了解、会调用函数即可。
☆ 例2-13: 运行下面代码前,可以结合 MATLAB 自行思考存储矩阵的方式,思考 ans1-ans6 ,对于 ans5-ans6 无需过于深究其原理,会调用函数即可。
clc,clear all,close all
% ans1
ans1 = sub2ind([3,4],2,3)
% ans2
[ans2_row, ans2_col] = ind2sub([3,4],5)
% ans3
ans3 = sub2ind([4,5],[2,2,3,3],[4,4,5,5])
% ans4
[ans4_row, ans4_col] = ind2sub([4,5],[4,5,6,7,8,9])
% ans5
ans5 = sub2ind([3,4,5],2,3,3)
% ans6
[ans6_dim1, ans6_dim2, ans6_dim3] = ind2sub([3,4,5],20)
分析:
对于ans1-ans2,下面这张图能让你更好地理解二维矩阵中的线性索引和下标索引(仅需掌握二维矩阵中即可,高维矩阵直接调用函数),ans3-ans4同理,区别只在于输入参数换成了一组索引。
d. 多元素访问(区域寻访)
对于矩阵内多个元素的访问,同样分为多下标索引的元素访问和单下标线性索引的元素访问。
多下标索引的矩阵元素访问时,使用冒号创建向量来选定某个维度中需要访问元素的下标,如果想要访问该维度下的所有元素,用冒号代替下标即可。例如对于一个 4 ∗ 5 4*5 4∗5大小的二维矩阵A来说:
· A(2:3, 4:5) 即访问矩阵A第2-3行、第4-5列的元素;
· A(2:3, : ) 即访问矩阵A第2-3行的所有元素;
· A(:, 5) 即访问矩阵A第5列的所有元素;
· A(1:2:4, 1:3:5)即访问矩阵A第1、3行,第1、4列的元素;
· A(:, : ) 即访问矩阵A的所有元素。
单下标线性索引的矩阵元素访问时,使用冒号创建向量来选定需要访问元素的单下标,如果想要访问整个矩阵的所有元素,用冒号代替下标即可。例如对于一个 4 ∗ 3 4*3 4∗3大小的二维矩阵A来说:
· A(2:4) 即访问矩阵A第1列第2-4行的元素(也就是线性索引下标2-4的元素);
· A(6) 即访问矩阵A第2行第2列的元素(也就是线性索引下标6的元素);
· A(1:4:12)即访问矩阵A第1行的所有元素(也就是线性索引下标1、5、9的元素);
· A(: ) 即访问矩阵A的所有元素。
由此也可以类推高维矩阵的多元素访问。对于高维矩阵,在访问时可能会出现访问的元素超过 MATLAB 能够显示的二维矩阵,这样的情况下 MATLAB 会按照 前文所述 的方式展示访问结果。
2.3.2.5 矩阵的基本操作
本小节介绍矩阵最基础的操作,为后续学习的矩阵内容做铺垫。本小节讲到的几种基本操作非常重要,需要灵活运用。
a. 提取
矩阵元素的提取本质上就是 矩阵元素的访问 。前文已述,这里不再赘述。
b. 合并
对于两个二维矩阵A、B来说,矩阵的合并分为水平方向合并和垂直方向合并。
水平方向合并要求两矩阵的行数相同。水平方向合并可以采用中括号的方式进行合并,中间以空格或逗号隔开,即 M = [A B];也可以使用horzcat(了解)函数进行合并,即 M = horzcat(A,B)。
垂直方向合并要求两矩阵的列数相同。垂直方向合并可以采用中括号的方式进行合并,中间以分号隔开,即 M = [A;B];也可以使用vertcat(了解)函数进行合并,即 M = vertcat(A,B)。
使用中括号合并矩阵本质上就是调用函数 horzcat 和 vertcat,如果不按照要求进行矩阵合并(也就是上两段中黄色高亮文字),MATLAB 可能会返回调用 horzcat 和 vertcat 函数时出错。
对于两个高维矩阵的合并,需要使用 cat 函数。
cat(dim, A, B):在指定的第 dim 维度上合并矩阵A、B,dim为一个正整数,指定维度。例如,当 A、B 为二维矩阵时,cat(1, A, B) 等价于 horzcat(A,B),cat(2, A, B) 等价于 vertcat(A,B)。
使用 cat 函数合并高维矩阵时同样也要注意对齐的问题,即两个合并矩阵在第 dim 维的长度应相同,否则无法合并。
此外,MATLAB 中有一些函数专门处理特殊的矩阵合并。下列函数仅需了解。
| 函数名称 | 功能 |
|---|---|
| repmat | repmat(A, m, n),将矩阵A复制 m*n 个,构造 m ∗ A r o w s m*Arows m∗Arows 行 n ∗ A c o l s n*Acols n∗Acols 列的新矩阵 |
| blkdiag | 使用已知矩阵构造新的对角化矩阵,即已知矩阵 A、B、…,构造新矩阵 M = [ A 0 . . . 0 0 B . . . 0 ⋮ ⋮ ⋱ ⋮ 0 0 . . . N ] M = \begin{bmatrix}A & 0 & ... & 0\\ 0 & B & ... & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0& 0 & ... & N\end{bmatrix} M=⎣⎢⎢⎢⎡A0⋮00B⋮0......⋱...00⋮N⎦⎥⎥⎥⎤ |
repmat([1 2;3 4],2,3)
blkdiag([1 1;1 1],[2 2 2;2 2 2;2 2 2],[3],[4 4;4 4])
c. 删除
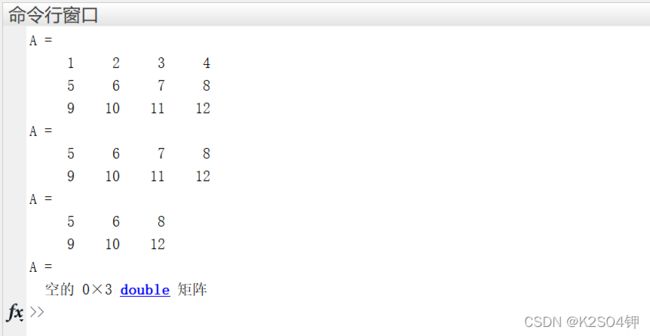
选定矩阵中的元素后,使用 中括号 [ ] 可以快速删除矩阵元素。
例如对于一个 3 ∗ 4 3*4 3∗4的矩阵 A 来说:
· A(1, : ) = [ ] 即删除矩阵 A 的第一行,并将结果赋给 A;
· A( : , 3) = [ ] 即删除矩阵 A 的第三列,并将结果赋给 A;
· A( : , : ) = [ ] 或 A( : ) 即删除矩阵 A 的所有元素,并将结果赋给 A 。
clc,clear all,close all
A = [1 2 3 4;5 6 7 8;9 10 11 12]
A(1,:) = [] % 先删除矩阵A第一行
A(:,3) = [] % 再删除矩阵A第三列
A(:,:) = [] % 最后删除矩阵A所有元素
d. 重组
使用 reshape 函数能快速将矩阵元素重组。
reshape(A, m, n):将矩阵的所有元素按照矩阵元素的存储顺序依次重组到一个大小为 m ∗ n m*n m∗n 的新矩阵里。对于高维矩阵同理。
这个函数能快速实现高维矩阵降维,也可以将低维矩阵里的数据转换到高维矩阵中。
clc,clear all,close all
A1 = [1 2 3 4;5 6 7 8;9 10 11 12]
B1 = reshape(A1,2,6) % 转换为2*6的矩阵
A2(1,:,:) = [1 2 3;4 5 6];
A2(2,:,:) = [7 8 9;10 11 12];
A2 % 2*2*3的高维矩阵
B2 = reshape(A2,2,6) % 降维到2*6的二维矩阵
2.3.2.6 查找矩阵中的元素
使用 find函数可以快速返回矩阵中符合要求元素的索引(行下标和列下标),返回的行、列下标均为行向量且一一对应。find函数的调用方式如下:
find(A):(不常用,了解即可)返回矩阵A中不为0元素的线性索引,该索引为一个列向量;
find(A, n, direction):(不常用,了解即可)若direction = ‘first’(默认),返回矩阵A线性索引前n个元素中不为0元素的线性索引,该索引为一个列向量;若direction = ‘last’(默认),返回矩阵A线性索引后n个元素中不为0元素的线性索引,该索引为一个列向量;
[row, col] = find(matrix):matrix为一个矩阵或者是某个表达式运算后的矩阵,返回matrix中不为0元素的索引,行下标赋值给row,列下标赋值给col,二者均为列向量。
使用 [row, col] = find(expr),我们可以快速查找矩阵中符合表达式 expr 要求的索引。下面给出了查找矩阵中某个元素的索引的方法:
查找矩阵中值为n的元素的行、列索引:
[row, col] = find(A(:,:) == n)
查找矩阵中第i行值为n的元素的列索引:
[~, col] = find(A(i,:) == n)
查找矩阵中第j列值为n的元素的行索引:
[row, ~] = find(A(:,j) == n)
这样的操作本质是将原有的矩阵A转化为符合要求的 logical 矩阵,由于find函数的功能即是返回输入矩阵中值不为0元素的索引,因此在这样的操作中,find函数就返回了 logical 矩阵中值为 logical 1 的元素的索引,也就是返回了符合表达式要求的元素索引。
如果需要在更复杂的表达式中求矩阵符合要求的元素索引,道理是一样的,只需要考虑怎么去设计find函数的输入矩阵,也就是考虑 [row, col] = find(expr) 中的 ‘expr’ 怎样设计才能满足需求。如果 ‘expr’ 进行运算的矩阵是原矩阵提取后的矩阵,则还应找到正确的映射关系,使经过 find 函数得到的索引通过这样的关系能正确地映射在原矩阵的索引。
☆ 例2-14 矩阵 A 为一个 6 ∗ 6 6*6 6∗6 大小的矩阵,矩阵元素的值为 1-10 的整数。对于该矩阵第 2-5 行、第 2-5 列的元素,找出值在闭区间 [3, 6] 的元素的线性索引。
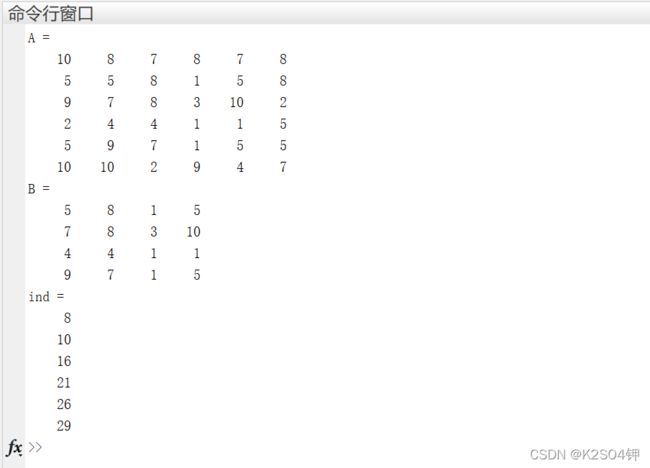
clc,clear all,close all
A = [10,8,7,8,7,8;5,5,8,1,5,8;9,7,8,3,10,2;2,4,4,1,1,5;5,9,7,1,5,5;10,10,2,9,4,7]
B = A(2:5,2:5) % 提取2-5行2-5列的矩阵,设为B
B = (B <= 6) & (B >=3 ); % 先将矩阵B转化为逻辑矩阵,值在3-6的元素设为逻辑1
[row,col] = find(B(:,:) == 1); % 找出矩阵B中值为逻辑1的元素下标,也就是符合条件的元素在B矩阵中的下标
row = row+1; col = col+1; % 由B矩阵的下标,线性映射到A矩阵的下标
ind = sub2ind(size(A),row,col) % A矩阵的下标索引转化为A矩阵的线性索引(ind即最终结果)
思考题2
☆ 思考题2-9: 计算下列表达式。
(1)设 t = 2 t=2 t=2,求 y = 2 s i n ( 0.3 π t ) 1 + 5 y=\frac{2sin(0.3\pi t)}{1+\sqrt{5}} y=1+52sin(0.3πt)的值;
(2)设 x = 2 x = 2 x=2,求 2 e x + 0.5 + l n 2 \sqrt{2e^{x+0.5}+ln2} 2ex+0.5+ln2的值;
(3)计算 y = 2 a r c s i n ( 3 4 ) + a r c o s ( 3 4 ) 3 ( l n 2 + l g 5 ) y=\frac{2arcsin(\frac{3}{4})+arcos(\frac{\sqrt {3}}{4})}{3(ln2+lg5)} y=3(ln2+lg5)2arcsin(43)+arcos(43)的值;
(4)设一角度(单位为度)为 θ \theta θ,在MATLAB中存储为变量theta,已知theta的正切值为2,编写程序求该角角度(单位为度)值和弧度(单位为rad)值,并计算该角的双曲余弦值。
☆ 思考题2-10: 结合函数句柄的知识点,构造函数句柄来表达函数: y = { ∣ x − 2 ∣ + x 2 e − x , x ⩽ 3 l n ( ⌊ x ⌋ ) + l g ( ⌈ x ⌉ ) + x 2 3 , x > 3 y=\left\{\begin{matrix} \frac{\left | x-2 \right |+x^2}{e^{-x}},x\leqslant 3\\ ln(\left \lfloor x \right \rfloor)+lg(\left \lceil x \right \rceil)+\sqrt[3]{x^2},x>3 \end{matrix}\right. y={e−x∣x−2∣+x2,x⩽3ln(⌊x⌋)+lg(⌈x⌉)+3x2,x>3,并代入 x = 2 x=2 x=2和 x = 5 x=5 x=5查看结果。
☆ 思考题2-11: 已知矩阵如下。按要求完成任务。
A = [1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 17 18 19 20]
(1)使用函数返回该矩阵的行数、列数、维度、总元素个数和占用存储空间大小;
(2)先删除矩阵的第4行,再删除矩阵的第3列,最后将矩阵 [ 0 0 0 ] \begin{bmatrix} 0\\ 0\\ 0\end{bmatrix} ⎣⎡000⎦⎤添加到经过前两个步骤处理后的矩阵 A 的第2列和第3列之间,得到矩阵 ans2;
(3)将第(2)问最终得到的矩阵重构为任意二维矩阵 ans3;
(4)将原矩阵 A 的线性索引 3-7 的元素依次替换为数值-1、-2、-3、-4、-5,再将第1-2行、第4-5列元素替换为0;
☆ 思考题2-12: 已知4行10列的矩阵A、B如下,按要求完成任务。
A = [9,5,2,10,4,8,1,6,9,7;7,1,3,10,10,4,2,1,1,8
4,3,5,5,4,3,10,3,1,7;6,2,1,5,2,5,10,4,2,5];
B = [6,7,8,5,6,7,4,7,5,3;3,2,1,5,6,4,10,6,3,2;
8,4,10,5,9,9,9,3,9,3;2,7,8,4,8,6,6,4,2,5];
(1)求矩阵A中元素值为3的行、列索引;
(2)求矩阵A的2、3行中元素值在 [3,6] (闭区间)的列索引;
(3)求矩阵A和矩阵B对应位置元素值相等的行索引、列索引;
(4)取矩阵A的2-5列形成新的 4 ∗ 4 4*4 4∗4大小的矩阵M,取矩阵B的6-9列形成新的 4 ∗ 4 4*4 4∗4大小的矩阵N,逐一比较矩阵M和矩阵N的对应位置,求矩阵M和矩阵N对应位置 M(i,j) > N(i,j) (i、j是1到4的整数)的元素在原矩阵A、B中的行索引、列索引。
部分思考题答案
思考题2-9
clc,clear all,close all
% 第一问
t = 2;
y1 = 2*sin(0.3*pi*t)/(1+sqrt(5))
% 第二问
x = 2;
y2 = sqrt(2*exp(x+0.5)+log(2))
% 第三问
y3 = (2*asin(3/4)+acos(sqrt(3)/4))/(3*(log(2)+log10(5)))
% 第四问
theta_deg = atand(2)
theta_rad = deg2rad(theta_deg)
y4 = cosh(theta_rad)
思考题2-10
clc,clear all,close all
y = @(x) (x<=3)*(abs(x-2)+x^2)/exp(-x) + ...
(x>3)*(log(floor(x))+log10(ceil(x))+x^(2/3))
ans1 = y(2)
ans2 = y(5)
思考题2-11
clc,clear all,close all
A = [1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 17 18 19 20]
% 第1问
fprintf('<<第一问>>\nans1_rows、ans1_cols分别返回矩阵A的行数、列数:\n')
[ans1_rows,ans1_cols] = size(A)
fprintf('ans1_dim返回矩阵的维度,ans1_numel返回矩阵的总元素数量:\n')
ans1_dim = ndims(A)
ans1_numel = numel(A)
fprintf('以下是矩阵A占用存储空间的大小:\n')
whos A
% 第2问
fprintf('<<第二问>>\nans2a-ans2c分别是该问题每个操作后的结果:\n')
ans2a = A;
ans2a(4,:) = []
ans2b = ans2a;
ans2b(:,3) = []
ans2c = [ans2b(:,1:2),[0;0;0],ans2b(:,3:4)]
% 第3问
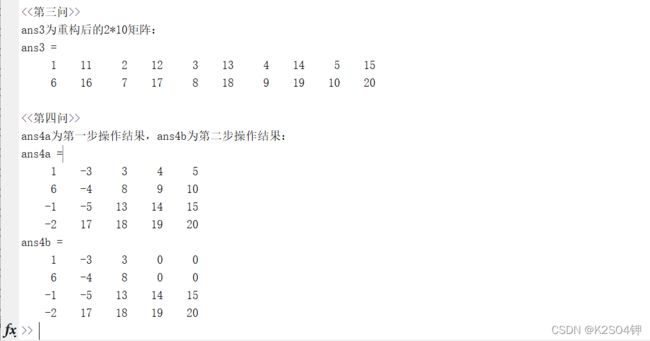
fprintf('\n<<第三问>>\nans3为重构后的2*10矩阵:\n')
ans3 = reshape(A,2,10)
% 第4问
fprintf('\n<<第四问>>\nans4a为第一步操作结果,ans4b为第二步操作结果:\n')
ans4a = A;
ans4a(3:7) = -1:-1:-5
ans4b = ans4a;
ans4b(1:2,4:5) = 0
思考题2-12
clc,clear all,close all
A = [9,5,2,10,4,8,1,6,9,7;7,1,3,10,10,4,2,1,1,8
4,3,5,5,4,3,10,3,1,7;6,2,1,5,2,5,10,4,2,5];
B = [6,7,8,5,6,7,4,7,5,3;3,2,1,5,6,4,10,6,3,2;
8,4,10,5,9,9,9,3,9,3;2,7,8,4,8,6,6,4,2,5];
% 第一问
[row1,col1] = find(A(:,:)==3); % row1为行索引,col1为列索引
row1 = row1',col1 = col1' % 为了方便展示,进行转置
% 第二问
[~,col2] = find(A(2:3,:)>=3 & A(2:3,:)<=6); % col2为列索引
col2 = col2' % 为了方便展示,进行转置
% 第三问
[row3,col3] = find(A(:,:) == B(:,:)); % row3为行索引,col3为列索引
row3 = row3',col3 = col3' % 为了方便展示,进行转置
% 第四问
[row4,col4] = find(A(:,2:5) > B(:,6:9)); % row4为行索引,col4为列索引
row4A = row4',col4A = (col4+(2-1))' % 在矩阵A中的行索引、列索引
row4B = row4',col4B = (col4+(6-1))' % 在矩阵B中的行索引、列索引
撰写:邓云泽、林耀
审核:华中师范大学HelloWorld程序设计协会工作人员
刘浩, 韩晶. MATLAB R2018a 完全自学一本通[M]. 北京:电子工业出版社. 2019. ↩︎