基于scipy的线性规划问题求解
基于scipy的线性规划问题求解
-
- 线性规划问题标准型
- 算例
- scipy求解
Scipy.optimize是Scipy中一个用于解决数学模型中优化类模型的子包,该子包中又包含了多个子功能模块见下表,不同方法不同条件求解最优化模型。本节介绍linprog对线性规划问题的模型建立与求解。

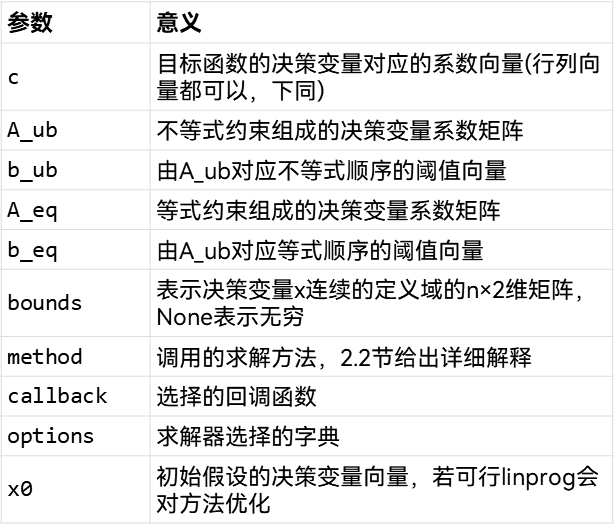
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='interior-point', callback=None, options=None, x0=None)
线性规划问题标准型
- 求的是 min
- 所有的约束为 <= 的形式
- 所有的变量均 >=0
算例
max x 1 + x 2 subject to x 1 − x 2 ≤ 0 − 1.5 x 1 + x 2 ≤ 0 50 x 1 + 20 x 2 ≤ 2000 x 1 , x 2 ≥ 0 \begin{align} \max \quad & x_1+x_2 \\ \text{subject to} \quad & x_1 - x_2 \leq 0\\ & -1.5x_1+x_2 \leq 0\\ & 50x_1+20x_2 \leq 2000 \\ & x_1, x_2 \geq 0 \end{align} maxsubject tox1+x2x1−x2≤0−1.5x1+x2≤050x1+20x2≤2000x1,x2≥0
scipy求解
from scipy import optimize as opt
import numpy as np
c = np.array([1, 1])
a = np.array([[1, -1], [-1.5, 1], [50, 20]])
b = np.array([0, 0, 2000])
res = opt.linprog(-c, a, b, bounds=((0, None), (0, None)), method="interior-point")
res
con: array([], dtype=float64)
fun: -62.49999900611451
message: 'Optimization terminated successfully.'
nit: 5
slack: array([ 1.24999998e+01, -3.33118066e-09, 3.18443099e-05])
status: 0
success: True
x: array([24.9999996 , 37.49999941])
message给出模型求解成功提示,
nit为迭代数,决策变量以x的数组形式返回,
最优值为fun。